ビット列のsideways additionというのは, 1のビットの数である.
(1 0 1 0 1 0 1 0 1) なら5である. (Henry WarrenのHacker's Delightではpopulation countという.) あるいは∑xi (xiは0または1) といってもよい.
またまたTAOCPの話題で恐縮だが, x1, x2, ..., x9の9ビットのsideways additionが次のように書いてあった.
x10=x1⊕x2⊕x3, x11=x4⊕x5⊕x6, x12=x7⊕x8⊕x9, x13=x10⊕x11⊕x12,
y1=⟨x1x2x3⟩, y2=⟨x4x5x6⟩, y3=⟨x7x8x9⟩, y4=⟨x10x11x12⟩
とすると
x1+…+x9=x13+2(y1+y2+y3+y4)
で得られる. x⊕y はxとyの排他的論理和; ⟨xyz⟩はx,y,zの多数決(TAOCPではmedianという)を表わす. x⊕y⊕zと⟨xyz⟩で全加算器になる.
非常に美しい式だが, 本当かとも思い, 早速やってみる.
(define base 10)
(define (sidewayadd xs)
(define (xor a b c) (modulo (+ a b c) 2))
(define (med a b c) (quotient (+ a b c) 2))
(let* ((x1 (modulo (quotient xs (expt base 0)) base))
(x2 (modulo (quotient xs (expt base 1)) base))
(x3 (modulo (quotient xs (expt base 2)) base))
(x4 (modulo (quotient xs (expt base 3)) base))
(x5 (modulo (quotient xs (expt base 4)) base))
(x6 (modulo (quotient xs (expt base 5)) base))
(x7 (modulo (quotient xs (expt base 6)) base))
(x8 (modulo (quotient xs (expt base 7)) base))
(x9 (modulo (quotient xs (expt base 8)) base))
(x10 (xor x1 x2 x3)) (x11 (xor x4 x5 x6))
(x12 (xor x7 x8 x9)) (x13 (xor x10 x11 x12))
(y1 (med x1 x2 x3)) (y2 (med x4 x5 x6))
(y3 (med x7 x8 x9)) (y4 (med x10 x11 x12)))
(+ x13 (* 2 (+ y1 y2 y3 y4)))))
(sidewayadd 000000111) => 3
(sidewayadd 111000111) => 6
なるほど. letの中の, 割ったり剰余をとったりしてx1, x2,...を作っているのは, (sidewayadd '(1 1 1 0 0 0 1 1 1))と書くのは面倒なので, (sidewayadd 111000111)としたいからである.
しかし落ち着いて考えてみると, アルゴリズムが正しいことは簡単に分かる.
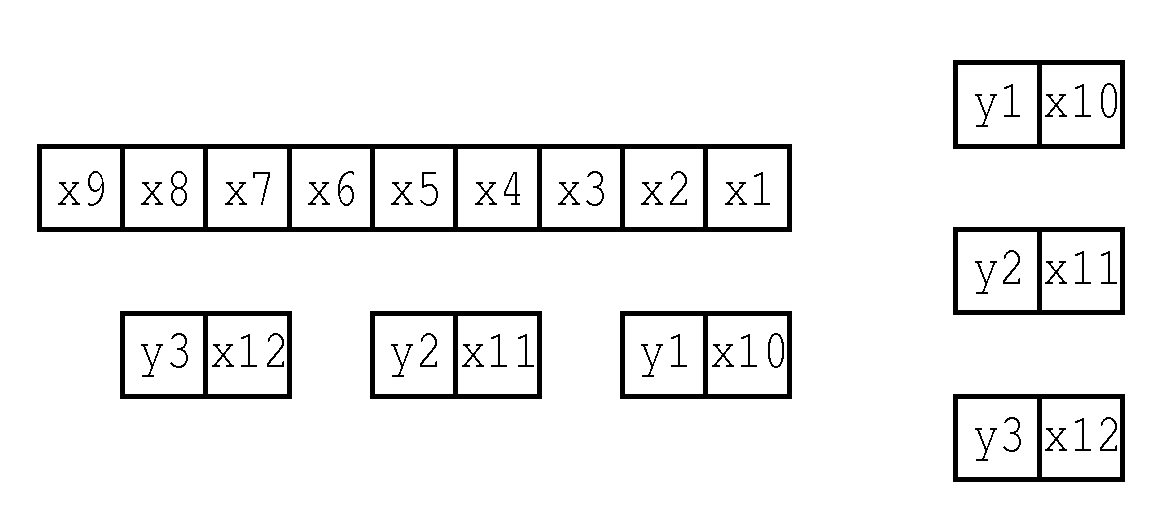
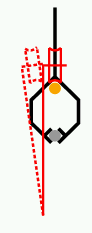
この図のように9ビットを右からx1,...,x9とする. 3ビットずつに区切り, その区間の和を求めると0から3までになるから, 2ビットで表現出来, それが下のx10,y1などである. x1,x2,x3の3ビットの二進法の和は, その1の桁(x10)はx1,x2,x3の排他的論理和だし, 10の桁(y1)はそれらの多数決だから, アルゴリズムにはそう書いてある. 次に3つの区間の3ビットの和が得られたとして, この和を取るわけだが, 和の1の桁はx10,x11,x12の排他的論理和である. 10の桁y1,y2,y3を足せばよく, それにx10,x11,x12からの繰上がり, すなわちそれらの多数決を足す. 10の桁だから2倍する.
と書いてしまえば, 当然なアルゴリズムであった.
この話題では, 思い出すことが2つある. 1つは英国ケンブリッジ大学のEDSACのライブラリのsideways additionで, 第2版に登場した.
EDSACの語長は35ビットだが, 36ビットと考えて6ビットの区間6つとする. ビットシフトやビット毎ANDや加算して, 6つの区間で並列にその区間の1の数を和を作る. 6までだから3ビットの範囲に収まる. つぎに105105...051(つまり5個の0と1が交互の列)を掛けると中央の6ビットの区間に総和が現れる仕掛けである.
この話はTAOCPのbitwise tricks and techniquesにも書いてある.
もう1つはパラメトロン計算機PC-1の語長が36ビットだったことに関係する. この36なる数は, 9ビット掛ける4なのだ. 9ビット毎にパリティをとり, エラー検出ビットを設ける計画であった. 3個のパラメトロンの信号のパリティは, 3重平衡変調器という回路で簡単に取れるはずで, それを2段用いれば9個のパリティが取れるというもくろみであった. そしてメモリーは1語当り情報36ビット, 検査用4ビット, 計40ビットで構成するはずであった. しかし3重平衡変調器が思ったほどにはうまく働かず, 結局パリティビットなしになった.
ところで, 最初の美しい式はy4まではBoole式だが, 最後に算術演算で足している. これは反則のようにも見えるが, y1+y2+y3+y4が実は(yiは0または1なので)再びsideways additionになり, 再帰的に回路を構成すればよい. Knuthの計算機MMIXには, 64ビットまでのオペランドのsideways addition SADDがあるが, かなりの回路になるであろう.


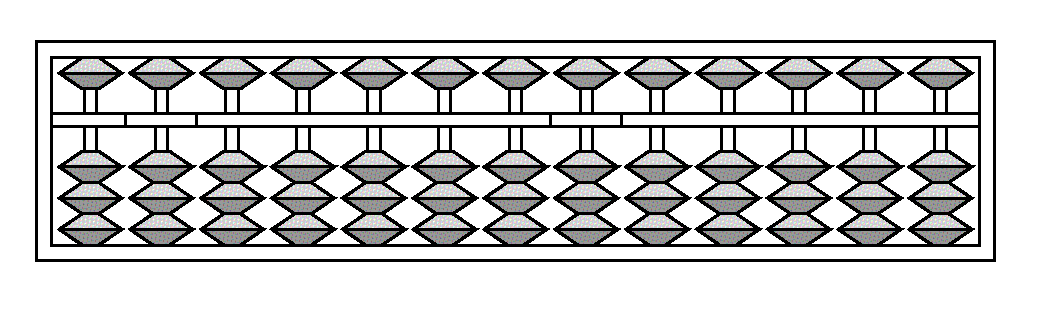
 八進法算盤
八進法算盤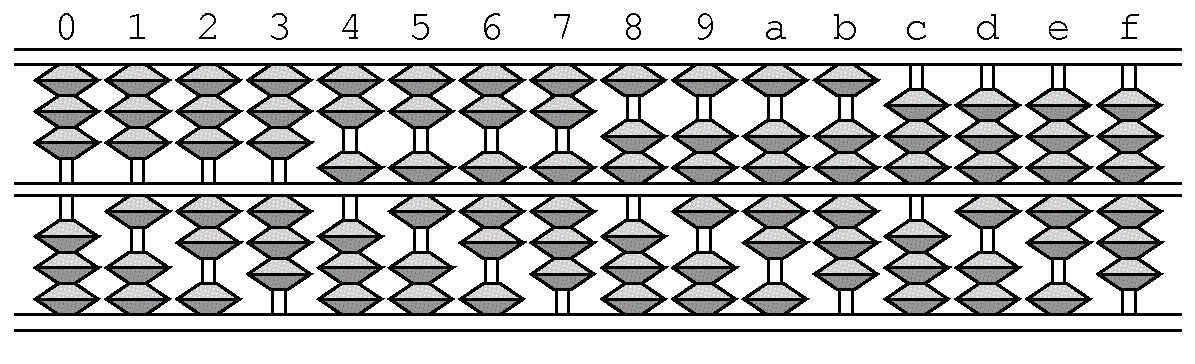
 HP16C
HP16C