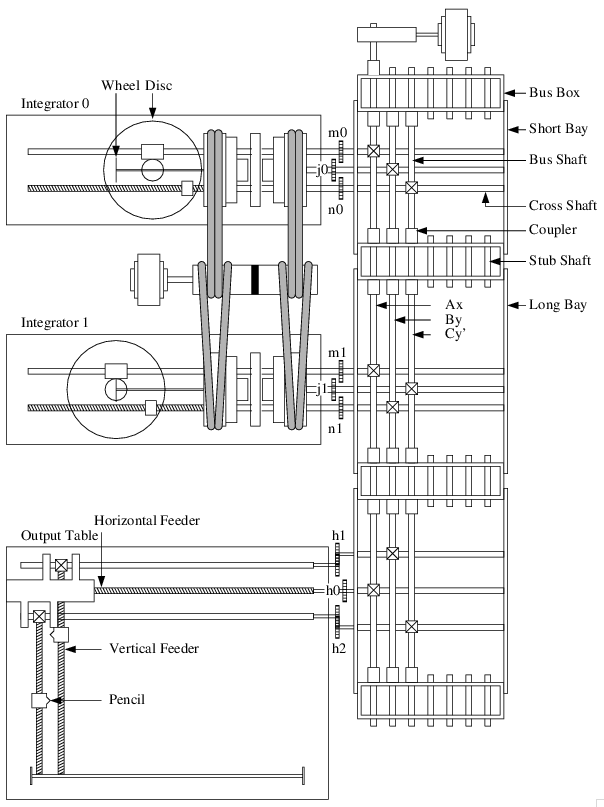
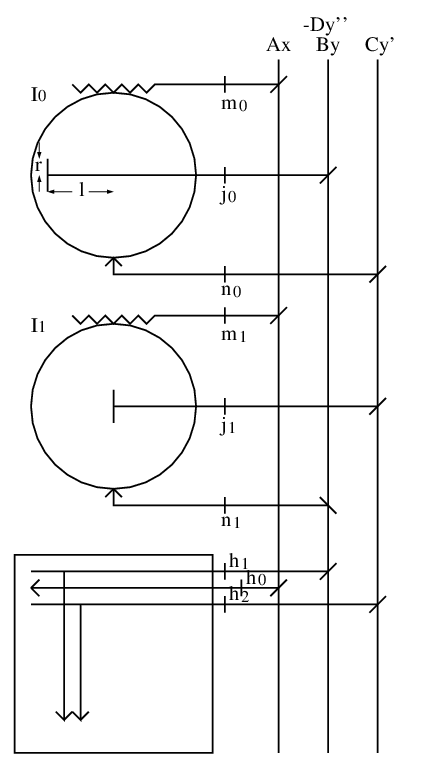
吉田光由の塵劫記にも, そろばんの絵とともとこの九九の説明がある. 塵劫記では割りのこえという. そういえば森口先生の「数理つれづれ」にもこの話があったことを思い出した.
要するに1桁の除数2≤d, 被除数n≤dに対する, 10n/dの商と剰余の表である.
使い方は後まわしにし, 2≤d≤9, 1≤n≤dについて商qと剰余rの表を作ろう.
(do ((d 2 (+ d 1))) ((> d 9)) (do ((n 1 (+ n 1))) ((> n d)) (let* ((nn (* n 10)) (q (quotient nn d)) (r (modulo nn d))) (display (list d n q r)))) (newline))実行すると(最上段のnと左端のdは後から私が書き込んだ. n=7から先は下に移動した.) 色分けについては下の変換規則A, B, ...などで説明する.
d\n 1 2 3 4 5 6
2(2 1 5 0)(2 2 10 0)
3(3 1 3 1)(3 2 6 2)(3 3 10 0)
4(4 1 2 2)(4 2 5 0)(4 3 7 2)(4 4 10 0)
5(5 1 2 0)(5 2 4 0)(5 3 6 0)(5 4 8 0)(5 5 10 0)
6(6 1 1 4)(6 2 3 2)(6 3 5 0)(6 4 6 4)(6 5 8 2)(6 6 10 0)
7(7 1 1 3)(7 2 2 6)(7 3 4 2)(7 4 5 5)(7 5 7 1)(7 6 8 4)
8(8 1 1 2)(8 2 2 4)(8 3 3 6)(8 4 5 0)(8 5 6 2)(8 6 7 4)
9(9 1 1 1)(9 2 2 2)(9 3 3 3)(9 4 4 4)(9 5 5 5)(9 6 6 6)
7 8 9
(7 7 10 0)
(8 7 8 6)(8 8 10 0)
(9 7 7 7)(9 8 8 8)(9 9 10 0)
が得られる. この4つ組を(d n q r)ということにする. このパターンにより読み方が変わるのが分かりにくい理由である.A. 各行の最後の(d d 10 0)は「d進の一十」と変換する.
B. (d n 5 0)のときは「d n天作の五」と変換する.
C. d=5, q=2n, r=0のときは, 塵劫記では「5 n倍作の2n」と変換するが, 掛け算より 森口先生の本のように「5 n加n」と変換しよう.
D. n=qのときは「d n下加r」と変換する.
E. それ以外は「d n q十r」と変換する.
これらの変換と算用数字を漢数字になおすと, 上の表は割り算の九九になる.
2(2 1天作の五)(2進の一十) 3(3 1 3十1)(3 2 6十2)(3進の一十) 4(4 1 2十2)(4 2天作の五)(4 3 7十2)(4進の一十) 5(5 1加1)(5 2加2)(5 3加3)(5 4加4)(5進の一十) 6(6 1下加4)(6 2 3十2)(6 3天作の五)(6 4 6十4)(6 5 8十2) (6進の一十) 7(7 1下加3)(7 2下加6)(7 3 4十2)(7 4 5十5)(7 5 7十1) (7 6 8十4)(7進の一十) 8(8 1下加2)(8 2下加4)(8 3下加6)(8 4天作の五)(8 5 6十2) (8 6 7十4)(8 7 8十6)(8進の一十) 9(9 1下加1)(9 2下加2)(9 3下加3)(9 4下加4)(9 5下加5) (9 6下加6)(9 7下加7)(9 8下加8)(9進の一十)しかし割り算をシミュレートするプログラムを書くには変換前の表が必要である.
さてこの九九の使い方だが, 下の図の左端は我々のやり方である.
この136割る3を塵劫記のアルゴリズムを使いそろばんではこう計算するらしい. (図の右 a,b,...)
3の段の九九を使うと覚えておいて, そろばんに136と置く.
矢印の百の桁に注目. 1なので三一三十一を使う. 1を商の3に変え, 下の桁の3に剰余の1を足して4にし(b), 注目の桁を下へ移す(c). 注目する桁の数がd未満のときはいつもこうする.
注目の桁は4なので三進一十を使う. 4から3を引き上の桁に1を足す(d). 「d進一十」を使う場合は注目の桁は下へ移さない.
注目の桁が1なのでまた三一三十一を使う. つまりこの桁を3にし下の桁の6に1を足し, 注目の桁を下へ移す(e).
一番下の桁は7だから三進一十が2回使えて十の桁は3から5になり, 一の桁に剰余の1が残る.
注目の桁が0の場合は下の桁へ移る. 九九の表にn=0の列(d 0 0 0)があると思えばよい.
このアルゴリズムをSchemeで書くとこうなる.
sはそろばんに対応する配列で, 塵劫記には一二三...九を割る例があるのでそれをやってみるつもりだ. 九九の表からd行目, sx列目を取り出す添字の計算が面倒だが, 九九の三角の表を一列のリストにしたからである.
(define kuku '(
(2 1 5 0)(2 2 10 0)
...
(9 1 1 1)(9 2 2 2)...(9 9 10 0)))
(define (div d x)
(display x) (display s) (newline)
(if (>= x (vector-length s)) s
(let ((sx (vector-ref s x)))
(cond ((= sx 0) (div d (+ x 1)))
((>= sx d) (vector-set! s x (- sx d))
(vector-set! s (- x 1) (+ (vector-ref s (- x 1)) 1))
(div d x))
(else (let* (
(ku (list-ref kuku (+ (/ (* d (- d 1)) 2) sx -2)))
(q (caddr ku)) (r (cadddr ku)))
(vector-set! s x q)
(vector-set! s (+ x 1) (+ (vector-ref s (+ x 1)) r))
(div d (+ x 1))))))))
(define s (list->vector '(0 1 2 3 4 5 6 7 8 9 0)))
(div 2 0)
塵劫記流に米十二万三千四百五十六石七斗八升九合を2で割ると, 下のようになる. 右端の九九やゼロスキップなどコメントは私が追加した.
0#(0 1 2 3 4 5 6 7 8 9 0) ゼロスキップ 1#(0 1 2 3 4 5 6 7 8 9 0) 二一天作の五 2#(0 5 2 3 4 5 6 7 8 9 0) 二進の一十 2#(0 6 0 3 4 5 6 7 8 9 0) ゼロスキップ 3#(0 6 0 3 4 5 6 7 8 9 0) 二進の一十 3#(0 6 1 1 4 5 6 7 8 9 0) 二一天作の五 4#(0 6 1 5 4 5 6 7 8 9 0) 二進の一十 4#(0 6 1 6 2 5 6 7 8 9 0) 二進の一十 4#(0 6 1 7 0 5 6 7 8 9 0) ゼロスキップ 5#(0 6 1 7 0 5 6 7 8 9 0) 二進の一十 5#(0 6 1 7 1 3 6 7 8 9 0) 二進の一十 5#(0 6 1 7 2 1 6 7 8 9 0) 二一天作の五 6#(0 6 1 7 2 5 6 7 8 9 0) 二進の一十 6#(0 6 1 7 2 6 4 7 8 9 0) 二進の一十 6#(0 6 1 7 2 7 2 7 8 9 0) 二進の一十 6#(0 6 1 7 2 8 0 7 8 9 0) ゼロスキップ 7#(0 6 1 7 2 8 0 7 8 9 0) 二進の一十 7#(0 6 1 7 2 8 1 5 8 9 0) 二進の一十 7#(0 6 1 7 2 8 2 3 8 9 0) 二進の一十 7#(0 6 1 7 2 8 3 1 8 9 0) 二進の一十 8#(0 6 1 7 2 8 3 5 8 9 0) 二一天作の五 8#(0 6 1 7 2 8 3 6 6 9 0) 二進の一十 8#(0 6 1 7 2 8 3 7 4 9 0) 二進の一十 8#(0 6 1 7 2 8 3 8 2 9 0) 二進の一十 8#(0 6 1 7 2 8 3 9 0 9 0) ゼロスキップ 9#(0 6 1 7 2 8 3 9 0 9 0) 二進の一十 9#(0 6 1 7 2 8 3 9 1 7 0) 二進の一十 9#(0 6 1 7 2 8 3 9 2 5 0) 二進の一十 9#(0 6 1 7 2 8 3 9 3 3 0) 二進の一十 9#(0 6 1 7 2 8 3 9 4 1 0) 二一天作の五 10#(0 6 1 7 2 8 3 9 4 5 0) ゼロスキップ 11#(0 6 1 7 2 8 3 9 4 5 0) ゼロスキップnが大きい場合, 二進の一十をn/2回使うので大変である. 実用的な割り算の九九には2の段には四進の二十, 六進の三十, 八進の四十が, 3の段には六進の二十, 九進の三十, 4の段には八進の二十があったらしい.
でもこれらは異端であって, 初めに書いた九九は最初の数が除数を示しているのに対し, ここで追加したのはそうなっていない.
そもそも八進に一十, 二十, 四十があり, 六進に一十, 二十, 三十があり, 四進や九進も複数できて使いにくかったのではないかと想像する.
この割り算にはもう一つ問題がある. 9の段など特にそうだが下加5とか下の桁に剰余を足すと繰り上げが生じることがある. それは注目している桁, 商のところに繰り上がる. その対策はあまり見たことがない.
上のようなシミュレーションを見ると, 12などという数が現れて驚く. しかしこういう場合の次は「d進一十」になるし, 繰り上げは高々1なので, すぐにdずつの引き算が始まり, 繰り上げは1回でなくなるから, さしたる問題にならないのかもしれない.
除数が2桁以上, つまり多重精度除数による除算については, またの機会に.