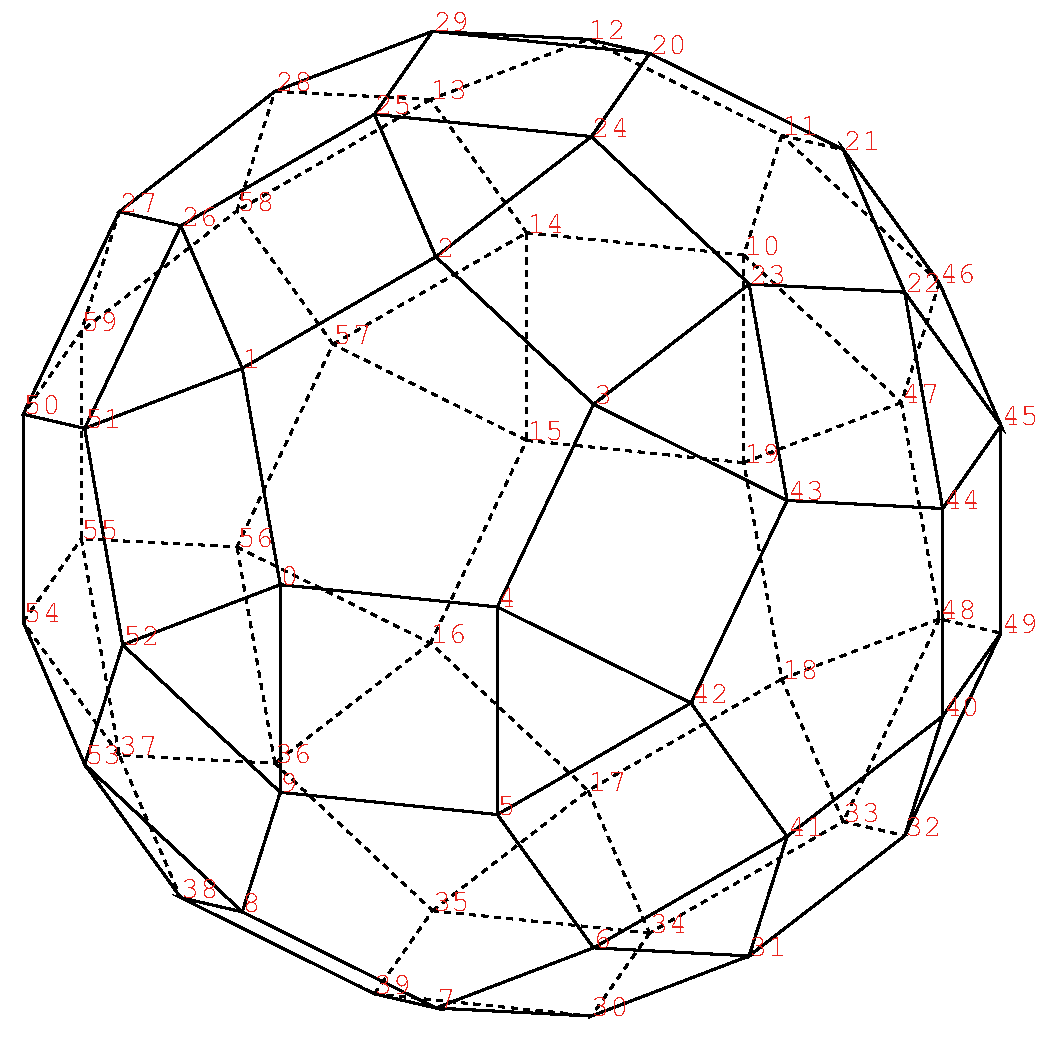
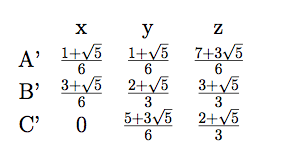元は立方体である. その各面の正方形を縮小し, どちらかに多少回転する. その方向により, 2つの相対の形がある.
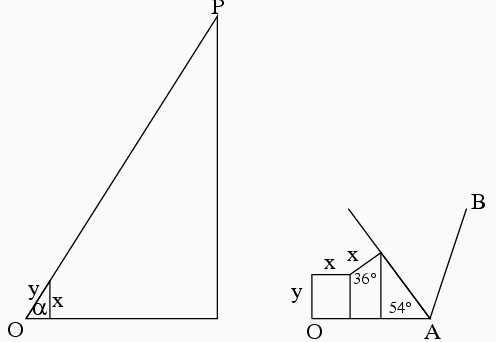
どのくらい縮小するか, どのくらい回転するかを計算しなければならない. そこで次の図のように考える.
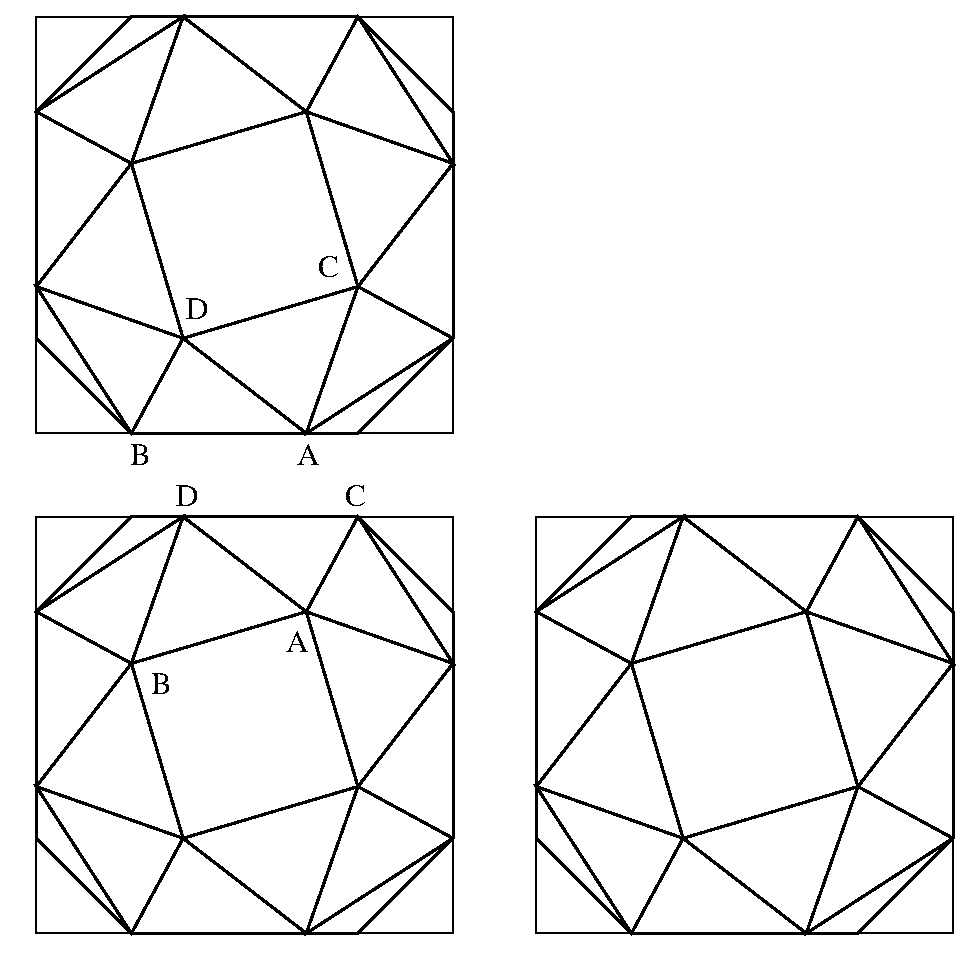
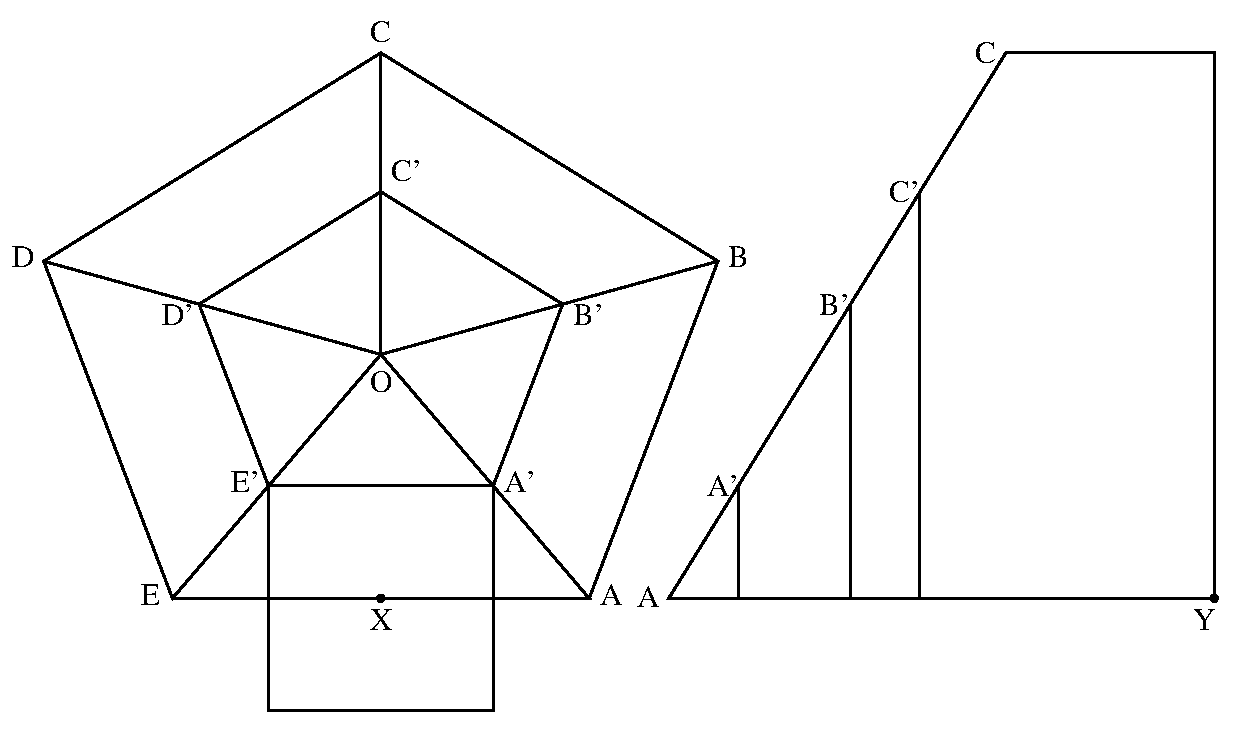
3つの似たような図があるが, 上が平面図(z方向から見た), 右下が側面図(y方向から見た), 左下が正面図(x方向から見た)である.
この立体は6の正方形と32の正三角形で被われる. 正方形と正三角形は辺を共有するから, すべての辺は同じ長さになる. それをdとする.
また, 座標の中心を立方体の中心にし, 立方体の1辺の長さを2とすると, A, B, C, Dの座標はそれぞれ
A(1,a,b)
B(1,-b,a)
C(a,b,1)
D(b,-a,1)
である. ABの距離の2乗はd2=(a+b)2+(a-b)2=2a2+2b2.
ACの距離の2乗はd2=(1-a)2+(1-b)2+(a-b)2.
従って, a+b+ab=1.
ADの距離の2乗はd2=(1-b)2+(2a)2+(1-b)2.
従って, 2b-a2=1, b=(1+a2)/2.
このbを上の式に入れると, a3+a2+3a=1. 3次式だから, 実数解はあるはずと思い, WolframAlphaの解いてもらうと, a=0.295598, 従ってb=0.543689, 念のため a+b+abを計算する.
(define a 0.295598)
(define b 0.543698)
(+ a b (* a b)) => 1.0000120414040001
計算は存外簡単であった. 球に内接の件は, どの頂点の座標も, 1とaとbで出来ているから, 当然である.
これさえ分かれば, 変形立方体を描くのはわけけない. いや1点落とし穴があった. 手前の面の座標から, 向こうの面の座標を得るのに, ついyz軸面の鏡面対称を使ったが, 正方形がが傾いているから, z軸に対して180度回転しなければならなかった.
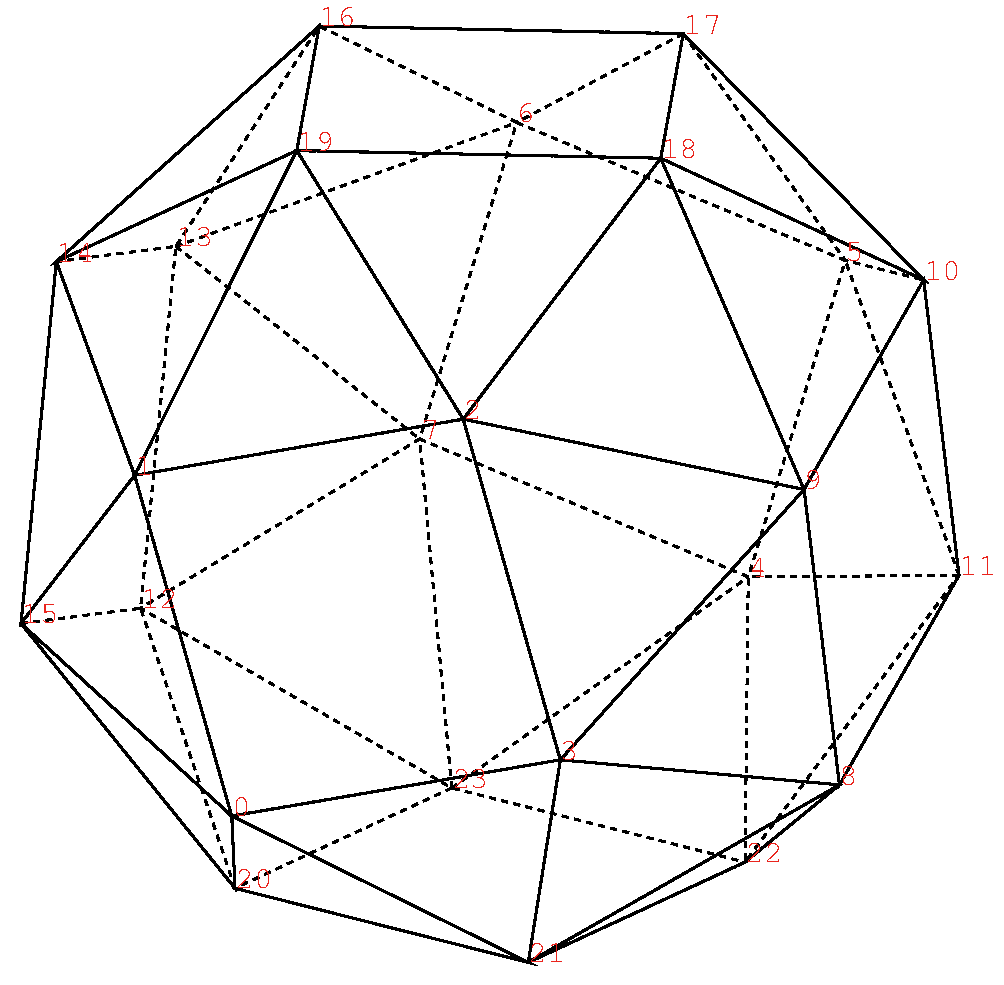
ところで, Archimedesたちが, こういう形になぜ気づいたかは不思議だ.