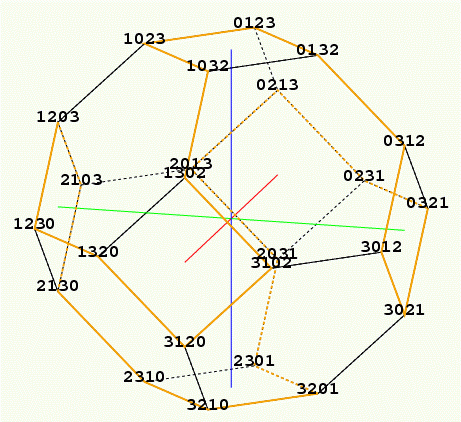
{0,1,2,3}の24通りの全順列を, 隣り同士の交換で実現しようというものである. 天辺にある0123を最初の順列とする. 左の2個を交換すると1023になり, それは天辺から左へ稜線を辿ると出会う1023である. 次は右の2個を交換し1032が得られる. このようにオレンジ色の線を一筆書きでたどれば全順列を通過するというわけである. これはこの立体のHamilton閉路(つまり全頂点を回って元へ戻る経路)になっている.
この立体は英語では"truncatedoctahedron", 日本語では「切頭八面体」というらしいが, いまいちな感じだ. これは正八面体の頂点を切り落としたものである.
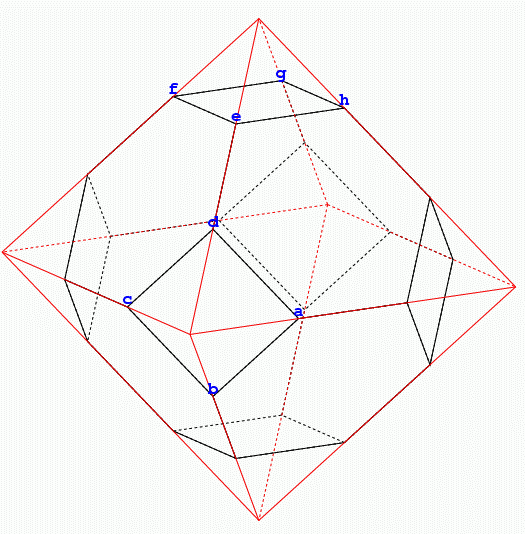
赤い線で示すのが正八面体で, 黒線のように切り取る.
ところでこの立体は, 正八面体の頂点を削れば出来るが, 立方体(正六面体)をの頂点を削っても出来る.
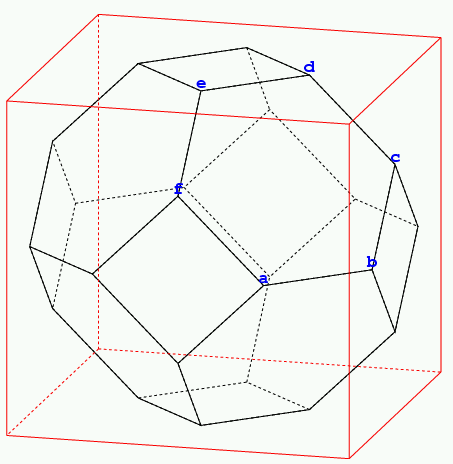
従って「切頭六面体」でもある. ただ削り取る量ははるかに多い. もともとこの立体には, 正方形が6枚, 六角形が8枚あるのだが, 正八面体の6つの頂点が6枚の正方形に辿り着き, 立方体の8つの頂点が8枚の六角形に辿り着く.
同様なものには, サッカーボールともいわれる, 「切頭二十面体」がある. (truncatedicosahedron)
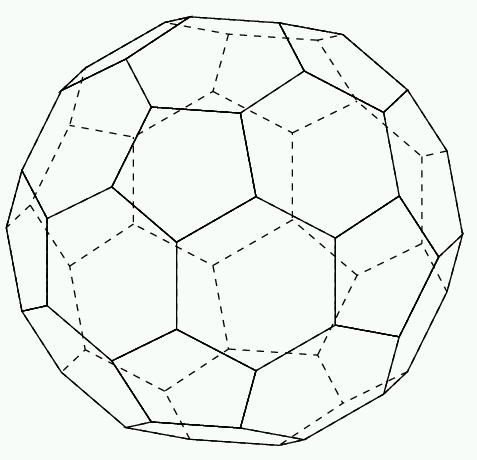
これも, 名前が示すように, 正二十面体の12個の頂点から削り, 12個の正五角形に辿り着くのと, 正十二面体の20の頂点から削り, 20個の正六角形に辿り着くのがある.
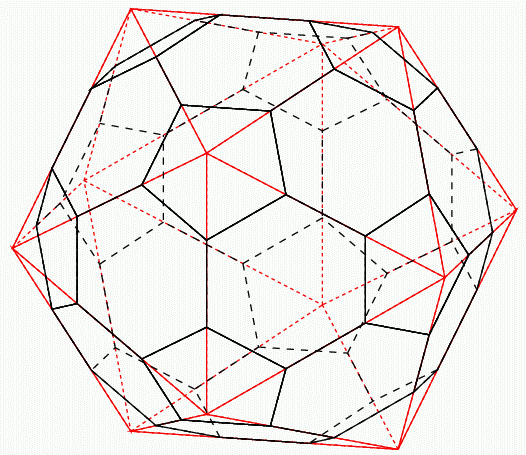
赤線で示す正二十面体の頂点から削って, 「切頭二十面体」を作る.
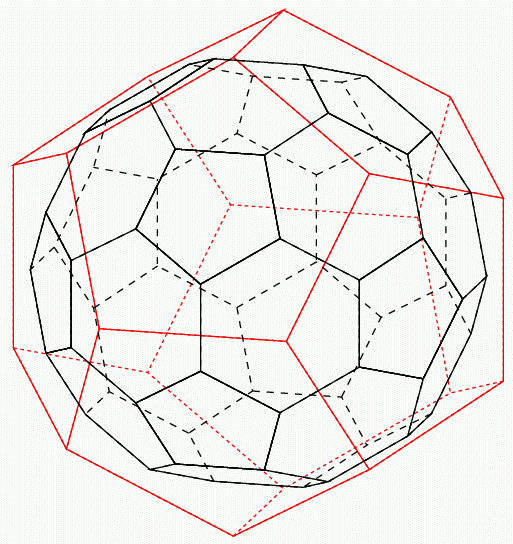
この方は赤線で示すのが正十二面体であり, その頂点から削り始めると, 正五角形の面が段々と削られ, 小さい正五角形が現れる.
さらに削り続けるとどうなるか. 正五角形は消滅して頂点になる. 一方正六角形は正三角形になる. 要するに正二十面体になってしまう. これが正十二面体と正二十面体は相対の関係にあることの証明である. 一方から他方へ移るちょうど途中にサッカーボールがあったのだ.
このことは, 最初の立体でも同じで, 正六面体と正八面体は相対の関係にあることが分かる. 正四面体は自分同士で相対の関係にある.
ではその途中はどういう立体か. その「切頭四面体」
(truncatedtetrahedron)を書いてみた.
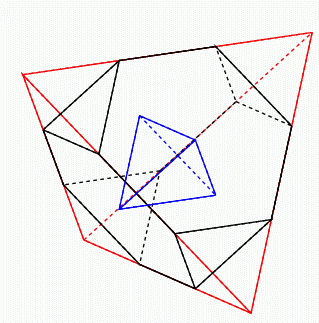
あまり見かけない立体ではあるが, 4個の頂点から現れた正三角形が4個の正三角形を六角形にして浸食し, ついには頂点になり, 正三角形の方が面になって, 面と頂点の機能を逆転した正四面体になる. この六角形がちょうど正六角形になった瞬間が上の図である. つまり削られて短くなりつつある元の稜と, 削りながら長くなりつつある新しい稜の長さはどこかで等しくなるのである. この点の座標の計算は簡単である. 逆転した正四面体を青線で示す.

0 件のコメント:
コメントを投稿