中央値関数は, 奇数個の引数を大きさの順に並べ, その中央の値を返す(平均値でないことに注意).
x≤y≤zの時 <xyz>=y.
あるグループで流行っている最中限ゲームみたいなものである.
論理関数としては, x,yを偽か真とする時, 常に反対するか常に賛成する偽か真のサクラの入力を加え, <偽xy>がxとyの論理積, <真xy>が論理和である.
実数値については, <-∞xy>はxとyの最小値, <+∞xy>は最大値になる.
こういう話題がいちおう終わってから,
m>0について,
x0⊕x1⊕...⊕x2m=<¬x0s1s1...s2m>
ここで, sj=<x0xjxj+1...xj+m-1¬xj+m¬xj+m+1...¬xj+2m-1>,
ただし, k≥1について, x2m+k=xkとする;
と書いてあった.
つまり, 何変数であっても, その排他的論理和がサクラ(定数)なしの2段の中央値関数で得られるのである. 美しい.
そもそも排他的論理和は単調関数ではないから, 中央値関数1段だけでは得られない. 3変数の排他的論理和, つまり全加算器もパラメトロンでは2段必要であった.
上の見事な式は, TAOCPによると, 量子化学が専門の佐々木不可止(ふかし)君が考えたという.
佐々木君は東大物理の学生時代に, 高橋研によく出入りしていて, 多数決論理に関心があったのは知っていたが, こういうことも考えたのかと驚いた. 北海道大学の化学科の教授を定年退職し, 苫小牧駒沢大学に移られたが, そこも退職の後, 惜しいことに2007年に他界された.
あの長々とした式は眼がくらくらするので, TAOCPにあったようにm=1とm=2について書き直すと
x0⊕x1⊕x2=<¬x0<x0x1¬x2><x0x2¬x1>>
x0⊕...⊕x4=<¬x0<x0x1x2¬x3¬x4><x0x2x3¬x4¬x1><x0x3x4¬x1¬x2><x0x4x1¬x2¬x3>>
となる.
この式をテストしてみよう. ます多数決関数mを定義する. nは否定をとる関数.
(define (m . xs)
(define (n x) (- 1 x))
(let ((l (length xs)))
(if (> (apply + xs) (/ (- l 1) 2)) 1 0)))
(m 1 0 0) => 0
(m 1 0 1) => 1
(m (n 1)(n 1) 1) => 0
すると5変数(m=2)の排他的論理和はこう書ける.
(define (ex x0 x1 x2 x3 x4)
(let ((s1 (m x0 x1 x2 (n x3) (n x4)))
(s2 (m x0 x2 x3 (n x4) (n x1)))
(s3 (m x0 x3 x4 (n x1) (n x2)))
(s4 (m x0 x4 x1 (n x2) (n x3))))
(m (n x0) s1 s2 s3 s4)))
(map (lambda (x) (apply ex (n2bs x 5))) (a2b 0 32)) =>
(0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1)
でどうやらよさそうだ.
パラメトロンは通常3入力止りだが, 5入力が許されるとしてこの回路はこう描ける.
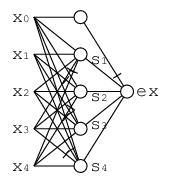
これをさらに納得すべく, s1,...s4や, その計算の元になっているx1+x2-x3-x4
などを, x0=0である前半の16個について出力してみよう. 自己相対関数なので, 半分やればいいことになっている.
xの否定は1-xと計算し, (l-1)/2の2と比較したから, 閾値と較べる値は, 本来は
x1+x2+(1-x3)+(1-x4)=2+x1+x2-x3-x4.
従って, 先頭の2を外して,
x1+x2-x3-x4
の和sumについてs1はsum≤0なら偽(x0=0を除外したから, 等号が要る), sum>0なら真である.
s1と添字がmだけ違うs3は, 足す項と引く項がちょうど反対だから, 和も正負逆で同じ値になる. こういう対を相棒といおう. ところで, 真が奇数個だと, 和が0になることはないので, 相棒同士の真理値は反対になり, x0がキャスティングボートをとって, exは真になる. すなわち排他的論理和である.
ところが, 真が偶数個だと, どこかに相棒同士で和が0になるものがあり, x0は0だから, sは2つとも偽になる. 先頭の¬x0が1を主張しても, 和が0でない他の相棒同士は打ち消し合い, この2個(あるいは4個)の0連合には勝てず, exは0になる.
+ s1 + s2 + s3 + s4 ex
0( 0 0 0 0 0 0 0 0 0)
1(-1 0 -1 0 1 1 1 1 1)
2(-1 0 1 1 1 1 -1 0 1)
3(-2 0 0 0 2 1 0 0 0)
4( 1 1 1 1 -1 0 -1 0 1)
5( 0 0 0 0 0 0 0 0 0)
6( 0 0 2 1 0 0 -2 0 0)
7(-1 0 1 1 1 1 -1 0 1)
8( 1 1 -1 0 -1 0 1 1 1)
9( 0 0 -2 0 0 0 2 1 0)
a( 0 0 0 0 0 0 0 0 0)
b(-1 0 -1 0 1 1 1 1 1)
c( 2 1 0 0 -2 0 0 0 0)
d( 1 1 -1 0 -1 0 1 1 1)
e( 1 1 1 1 -1 0 -1 0 1)
f( 0 0 0 0 0 0 0 0 0)
左端は行数である. 各行のかっこ内の9個の値は, 左からx1+x2-x3-x4, s1, x2+x3-x4-x1, s2, x3+x4-x1-x2, s3, x4+x1-x2-x3, s4, exである. 偶数個の場合, どの対で和が0になるかを調べたのが下だ. 赤の-は, x1とx2の和がx3とx4の和に等しい(つまりs1s3が0になる)場合, 青の-は, x2とx3の和がx4とx1の和に等しい(つまりs2s4が0になる)場合である.
0(0 0-0-0-0-)
1(0 0 0 0 1 )
2(0 0 0 1 0 )
3(0 0 0-1 1-)
4(0 0 1 0 0 )
5(0 0-1-0-1-)
6(0 0-1 1-0 )
7(0 0 1 1 1 )
8(0 1 0 0 0 )
9(0 1-0 0-1 )
a(0 1-0-1-0-)
b(0 1 0 1 1 )
c(0 1 1-0 0-)
d(0 1 1 0 1 )
e(0 1 1 1 0 )
f(0 1-1-1-1-)
和が0になる対は本当にあるか. こういう図を描いてみた.
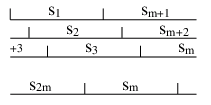
いま真というか1の数は偶数である. s1とsm+1の範囲で1の数が同じであれば, 一発で和が同じところは見つかったわけでハッピーだ.
一方, s1がオール0でsm+1がオール1なら, 左の密度は0, 右の密度は1. そこで図の下へs2, s3のように加算の範囲をずらしていけば, どこかで2つの範囲の1の数が一致する, 同じ密度になる場所があり, そこで赤や青の-が引ける対が見つかるはずである(平均値の定理を習ったのは高校生の時だっけ).
こういうわけで, 偶数の場合はexが偽になるのである.
「なるほど」であった.
実はサクラを使うと, どんな関数でも2段の中央値関数で作れるが, そのことはいずれ.
