この問題はいろいろなところに書いてある. 前述のSICPや, コンピュータの数学の他, G. PolyaのHow to Solve It(如何にして問題を解くか)にもあり, 私がたまたま持っている, PolyaとTarjanの1978年のStanfordでの講義ノート, D.R.Woods, Notes on Introductory Combinatoricd(STAN-CS-79-732)にも出ている.
SICPの記述はこうだ
50セント, 25セント, 10セント, 5 セント, 1セントがあるとして1ドルの両替にはどのくらいの場合があるか. つまり, 金額に対して両替の場合の数を計算する手続きは書けるだろうか.
この問題は再帰的手続きとして単純な解がある. 使える硬貨をある順に並べたとしよう. すると次の関係が成り立つ:
n種類の硬貨を使う, 金額aの両替の場合の数は:
• (a)最初の種類の硬貨以外を使う, 金額aの両替の場合の数, 足す
• (b)dを最初の硬貨の額面金額[denomination]として, n種類の硬貨を使う, 金額a-dの両替の場合の数
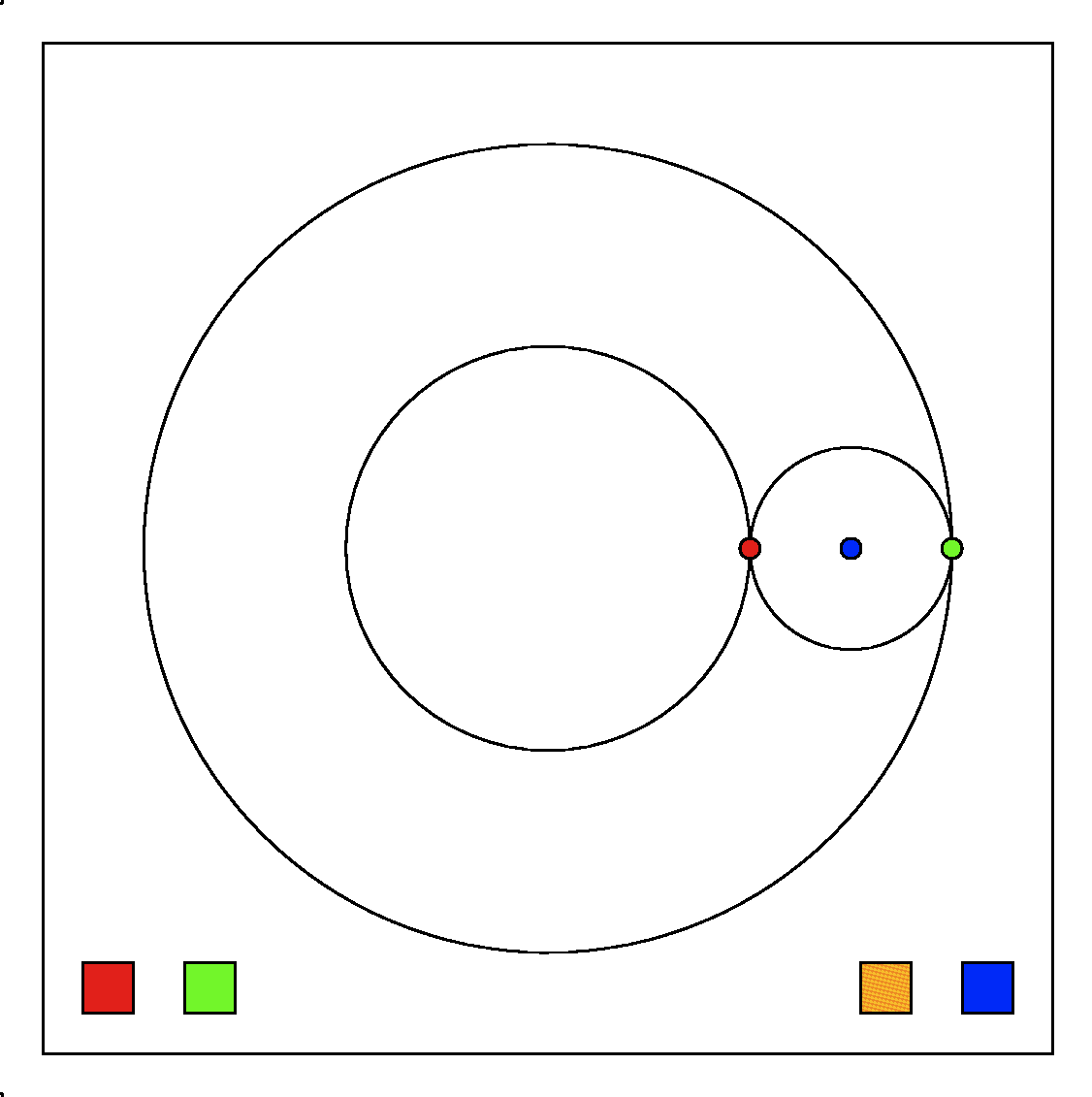
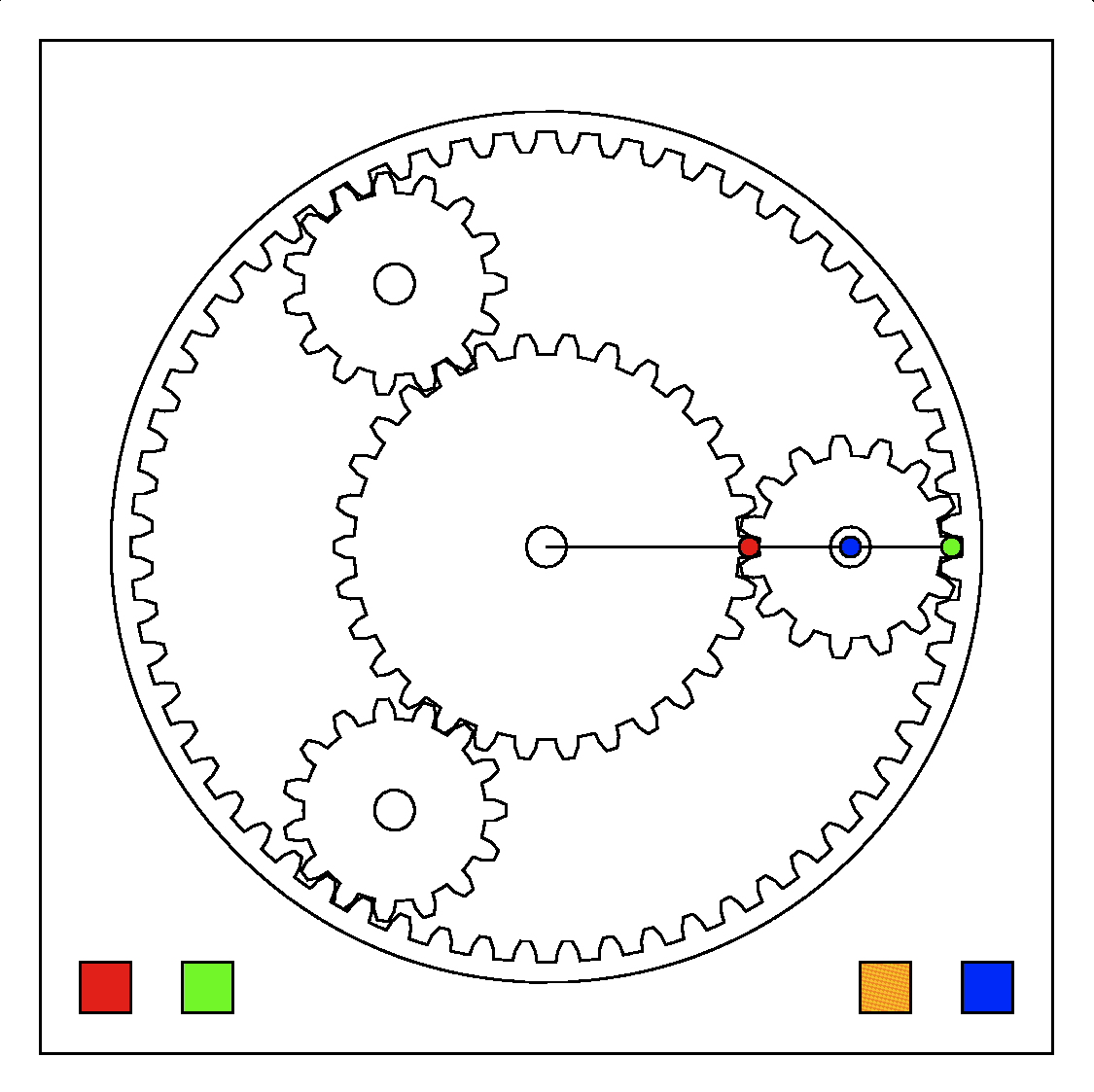
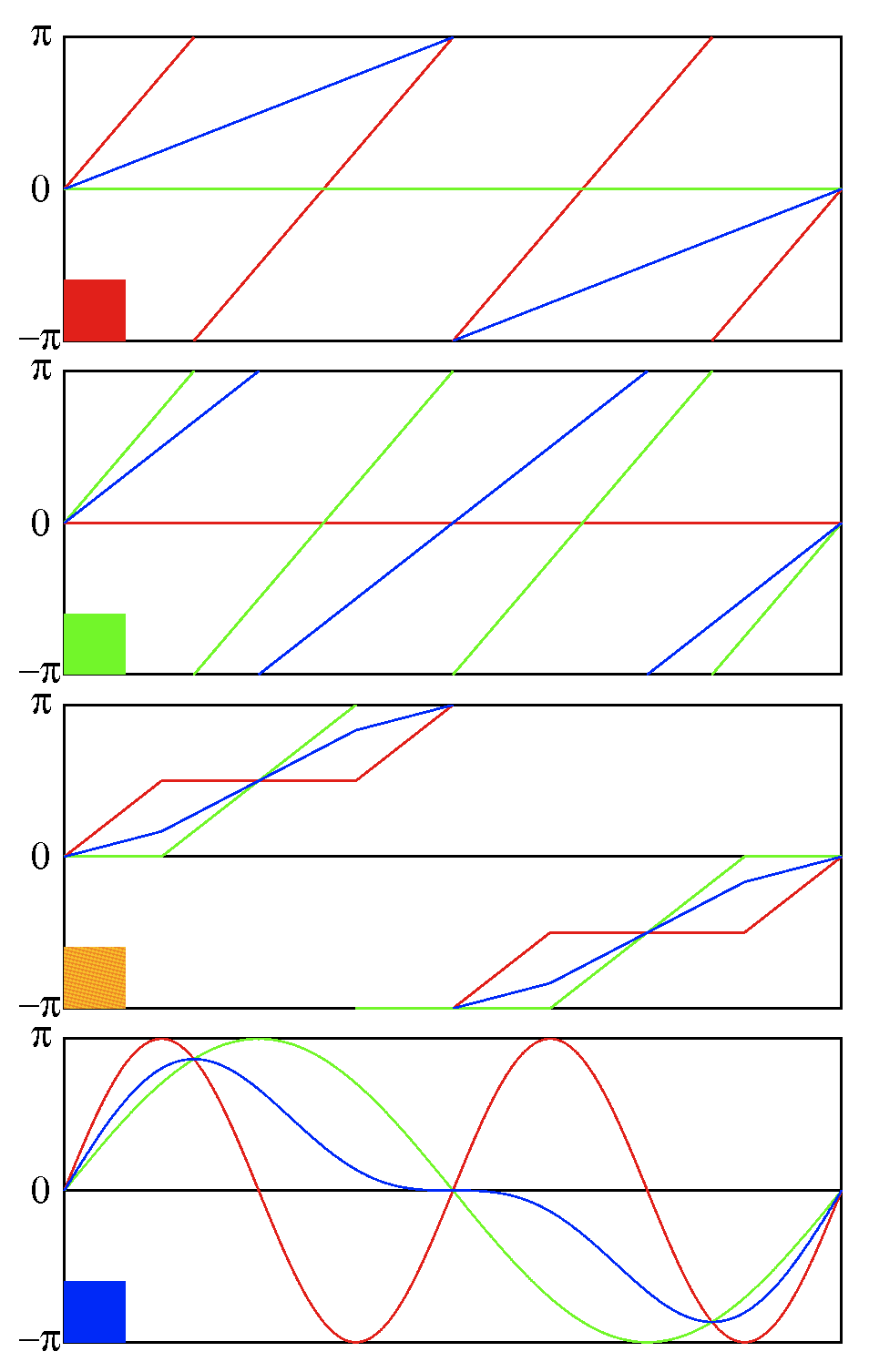
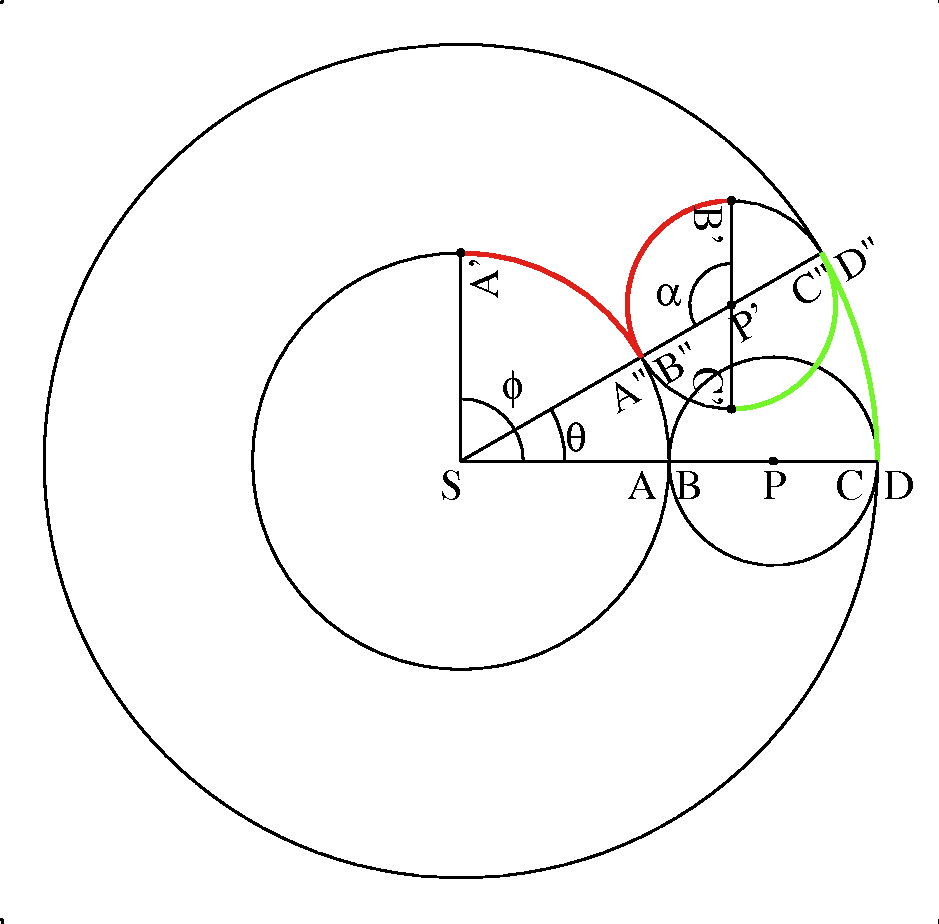
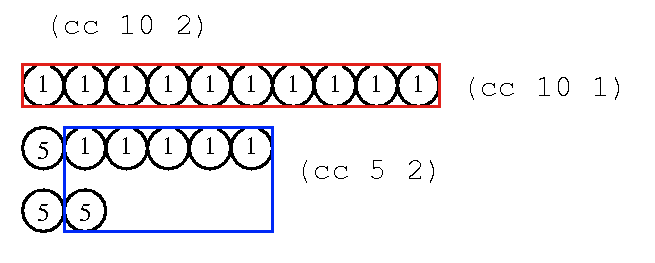
つまり1セントと5セントの2種類の硬貨で10セントにするには, 最初の種類の硬貨は5セントであり, 5セント以外の硬貨, つまり1セントで10セントにする場合の数(下の図で赤枠の場合)と, 5セントと1セントで10セントから5セント引いた5セントにする場合の数(青枠の場合)の和である.
また再帰の終わり
• (c)aがちょうど0なら, 両替の場合の数は1
• (d)aが0より少なければ, 両替の場合の数は0
• (e)nが0なら, 両替の場合の数は0
も考えなければならず, 結局プログラムは以下のようになる.
(define (count-change amount)
(cc amount 5))
(define (cc amount kinds-of-coins)
(cond ((= amount 0) 1) ;(c)
((or (< amount 0) (= kinds-of-coins 0)) 0);(d)と(e)
(else (+ (cc amount ;(a)の場合
(- kinds-of-coins 1))
(cc (- amount ;(b)の場合
(first-denomination kinds-of-coins))
kinds-of-coins)))))
(define (first-denomination kinds-of-coins)
(cond ((= kinds-of-coins 1) 1)
((= kinds-of-coins 2) 5)
((= kinds-of-coins 3) 10)
((= kinds-of-coins 4) 25)
((= kinds-of-coins 5) 50)))
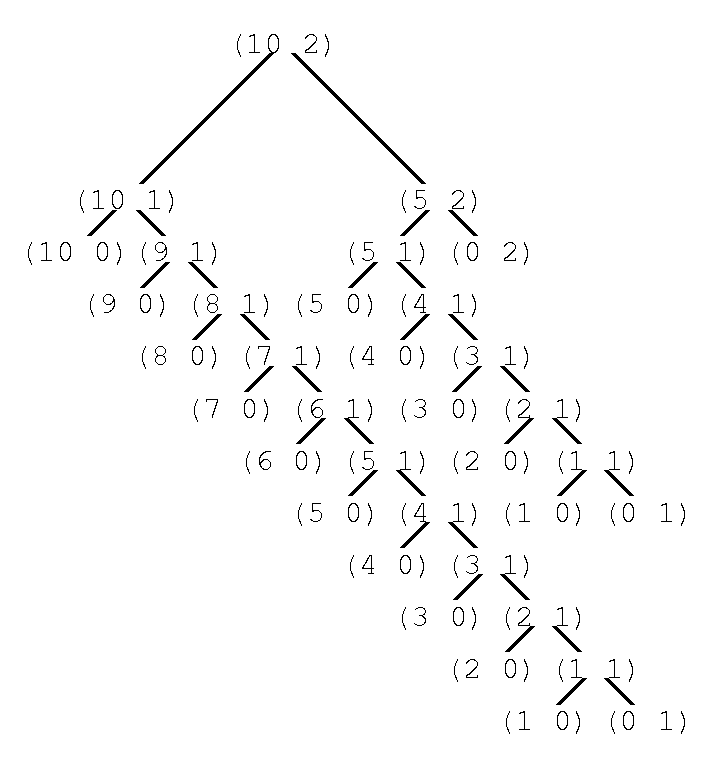
10セントの両替で, ccの呼ばれ方を図にすると下のようになる. 頂点の(10 2)はamountが10, kinds-of-coinsが2でccが呼ばれるの意. 左下(10 1)への枝は(a)の下請け, 右下(5 2)への枝は(b)の下請けであり, さらに下請けが次々と呼ばれることを示す. さらに右下方向へ延びる枝が, 図には全体で3本見えるが, この最後が(c)の1通りを返してきて, 結局35回呼ばれ, 3通りになる.
このプログラムの, 100セントの両替では, 関数ccは 15499回呼ばれた. その解析がこの表である.
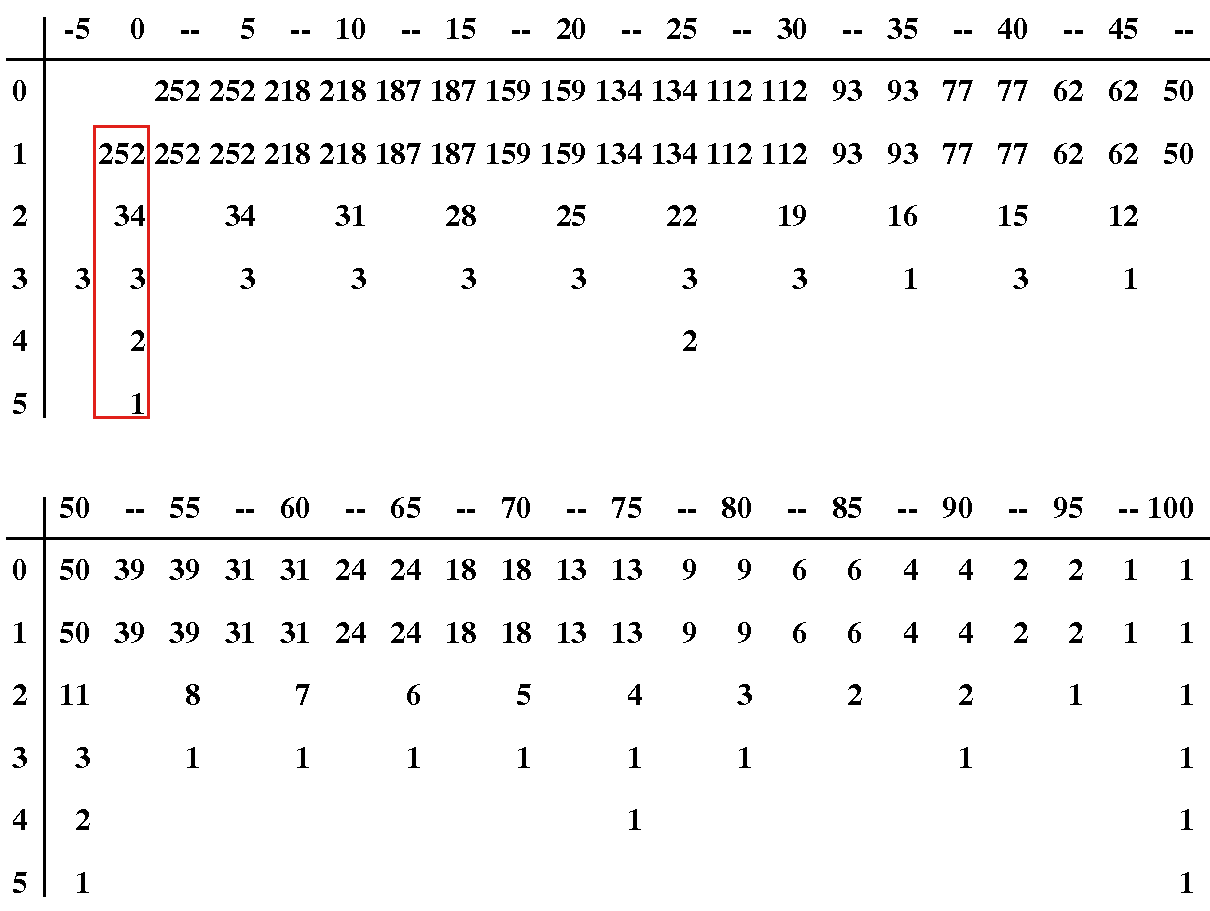
表の横はamount, 縦はkinds-of-coinsで, 横の見出しの「--」はその間の数, つまり0と5の間なら, 1,2,3,4のことである. amountは硬貨3種類のときに-5で3回呼ばれる. これは(cc 5 3)の時で, 5セントから10セントを引こうとして生じる.
この表の数値を全部足すと, 15499になる. また数値の入っている場所は250個所ある. つまり250通りで呼ばれるのである. 赤枠内のamount=0の欄を足すと, 解の292が得られる.
メモ化
これとかFibonacci数の計算のプログラムのような再帰プログラムでは, 同じ引数で関数を何回も呼ぶことによくなる. 上の計算でも引数の異なる呼出しは, 250回である. こういう時には, メモ化という手法が有効である.
小学生の頃, 長い割り算(商の桁数が多い)をするなら, まず除数の2倍, 3倍,..., 9倍の表を作ってから割り算の取り掛かったが, メモ化は表を新しい引数の組で関数を計算するたびに作るのである.
SICPでは, 3.3.3節の最後にメモ化の話題がある. それに倣って, memo-ccを作ってみた.
(define (make-table) ;和訳SICP 159ページにあるmake-table
(let ((local-table (list '*table*)))
(define (lookup key-1 key-2)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(cdr record)
false))
false)))
(define (insert! key-1 key-2 value)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! local-table
(cons (list key-1
(cons key-2 value))
(cdr local-table)))))
'ok)
(define (dispatch m)
(cond ((eq? m 'lookup-proc) lookup)
((eq? m 'insert-proc!) insert!)
(else (error "Unknown operation -- TABLE" m))))
dispatch))
(define (memoize f) ;和訳SICP 160ページのmemoizeを2次元化
(let ((table (make-table)))
(define get (table 'lookup-proc))
(define put (table 'insert-proc!))
(lambda (x y)
(let ((previously-computed-result (get x y)))
(or previously-computed-result
(let ((result (f x y)))
(put x y result)
result))))))
(define memo-cc ;和訳SICP 22ページのccをメモ化
(memoize (lambda (a k)
(set! cccount (+ cccount 1))
(cond ((= a 0) 1)
((or (< a 0) (= k 0)) 0)
(else (+ (memo-cc a (- k 1))
(memo-cc (- a (first-denomination k)) k)))))))
これでやってみると, memo-ccが呼ばれたのはちょうど250回であった.