軌跡作図器

JavaScriptによるアニメーションができた.



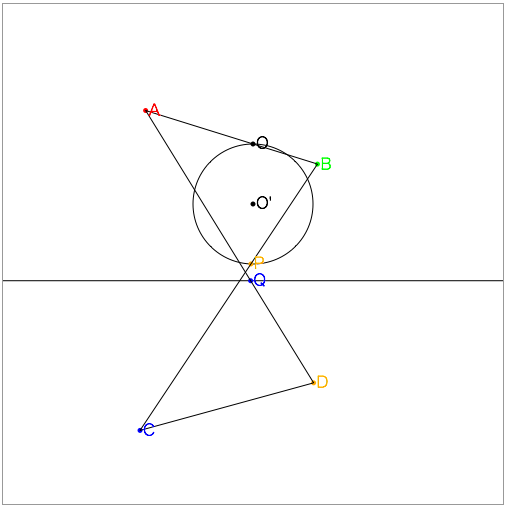
ここにあります.

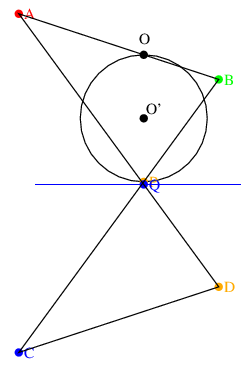
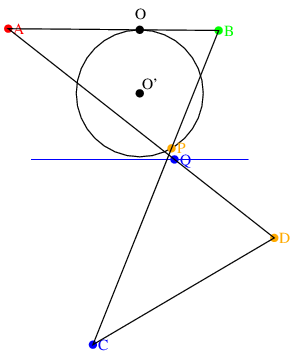
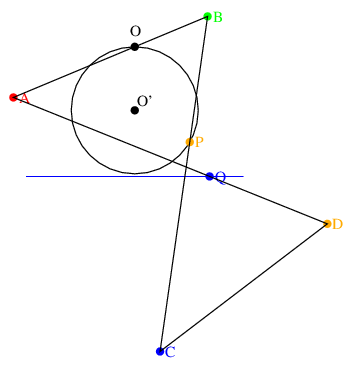
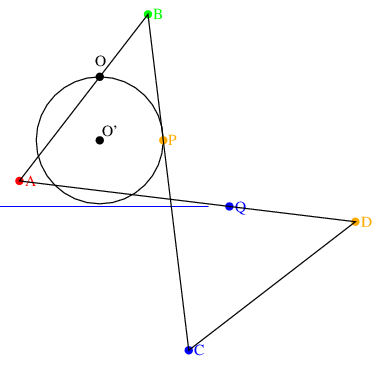
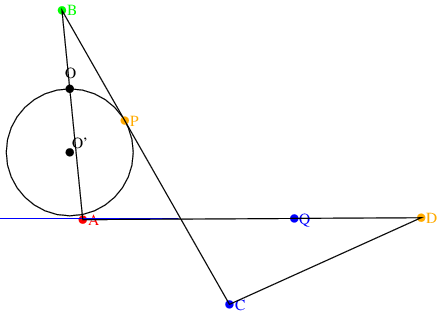
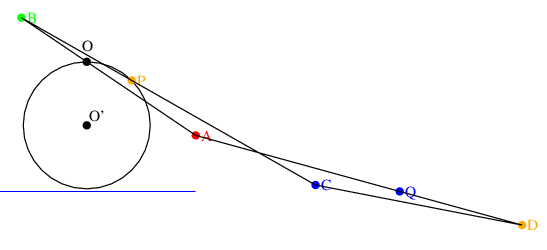
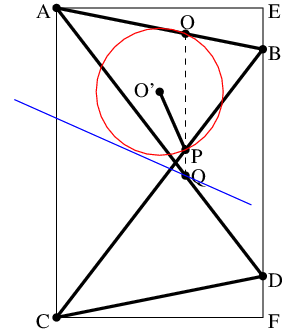
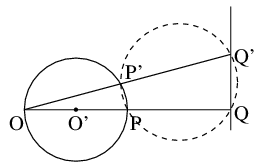
PがO'を中心とする円上を移動すると, Qは直線上を移動する.

軌跡作図器

先日のブログの最後にJavaScriptで動かしたいと書いた. まだそこまではいっていないが, Pの位置を変えるとQがどう動くが調べたくなって, PostScriptでプログラムを書いた.

方針としてはこうだ. AB, AO, ADの長さを決める. O, O'の位置を決める.

OO'の長さに等しくO'Pをとるわけだが, つまりO'を中心とする半径OO'の円上をPが動くわけだが, Oの反対側をO''とし, ∠O''O'Pを0から順に増やすことで, Pの位置を決めることにした.

OとPの位置やOBとPBの長さが分っているので, Bの位置が決まる. Bが決まるとAが決まり, BとPが分るからCも決まる. AとCからの長さが分っているから, Dの位置が決まり, Qも得られる.

このようにして, ∠O''O'Pを0°, 30°, 60°, 90°, 120°, 135°と変えて描いたのが次の図である.


0°


30°


60°


90°


120°


135°

この先Pはどこまで進めるかというと, OBとPBの長さが決まっているから, OPの間隔がPB-OBになったときに一直線になって以後破綻する.

軌跡作図器

學士會会報No.912 (2015-III)の表紙の図に興味をもった. 説明には独国マルチン・シリング(ハーレ社)製「軌跡作図器(Serie XXIV, Modell nr.11)」とあるが, それに続く説明は要領を得ないので改めて説明したい.

同じような図をネットで探して頂いてきたのが次の図だ.(http://goo.gl/Fpfcqt)



リンクABとCDの長さは等しく, ADとBCの長さも等しい. A,B,C,Dはピボットで連結されていて角度は変わる. AB, CB, ADのそれぞれをm : (1-m)に内分した点をO,P,Qとする(0 < m < 1).

Oは固定点で, ABはOを支点に回転する. PにPO'がOO'に等しくなるようなリンクPO'を取付け, O'も固定する. つまりPはO'を中心に円を描き, この円はOを通る.

こうしてPが円(の一部)を描くと, Qは直線の軌跡を描くという道具であった(Hartのinversorという名前である).

上の図を次のように書き直す. 太線がリンク機構である. 三角形ACBと三角形CADは逆向きだが合同だから, ACとBDは平行. ABDCは等脚台形になる. OPQは一直線でこれもACに平行.



BD上にA, CからACに垂線を立ててE,Fとする. EB=DFだから
AC×BDはEF×BD=(ED+EB)×(ED-EB)=ED²-EB².
ED²+AE²=AD²
EB²+AE²=AB²
だから
AC×BC=AD²-AB²
AO/AB=CP/CB=AQ/AD=mだから
OP=m×AC, OQ=(1-m)×BD
従って
OP×OQ=m×(1-m)×(AD²-AB²)=一定.

OP'×OQ'=OP×OQ=一定 でP'がOPの中点O'を中心とする円を動くと, Q'はQでOQに直交する線上を動く.



上の図で∠OP'P=∠R. ∠PQQ'=∠R だから4点PQQ'P'は円周上にあり, 方冪の定理(定点を過ぎる直線が定円と交わるとき, 定点より2つの交点までの長さの積は一定) によりOP'×OQ'=OP×OQ.

そのうちJavaScriptで動かしたいと思う.

SATソルバ

TAOCP 7.2.2.2にはSATソルバのアルゴリズムがいくつか登場する.

今回はそのうちAlgorithm 7222Aを話題としたい. ただこのアルゴリズムの背景を初めから述べるのは大変なので, TAOCPのその辺を読んである読者を対象に書くことで勘弁して貰いたい.

TAOCPのアルゴリズムは自然言語であるだけでなく, 非常に簡潔な記述なので, 前後の説明をよく理解していないと, なんのことだか分からないことが多い. そういう場合にSchemeで記述したこのブログのプログラムは理解の助けになのではないか. とにかく実際に動くプログラムとして存在するから だ.

TAOCPにも, あるデータを例としての説明はある. 7.2.2.2-6と7の式



で, (6)は充足不能, (7)は充足可能な例である.

まず(7)について, 次のようなデータを用意する.



配列L, F, B, Cは添字が0から30で, Lには(7)の節が置いてある. L(10)から始まる9,7,3は(7)の最後の節の3-,4-,1-を4,3,1の順にし, 正のリテラルは変数番号を2倍し, 負のリテラルは2倍して1足したものなので, 9,7,3になっている. Cの対応する場所の7は, 7番目の節を示す.

L(13)以降も同様である.

FとBは両方向リンクで, F(2)つまりリテラル1+が現れる場所はL(30)であり, F(30)=24は次がL(24)であることを示す. Bは逆向きの情報である.

リンク構造なのは, リテラルや節を削除/挿入するのに便利なためである.

C(2)からC(9)まではそれぞれのリテラルが何個あるかを示す.

それらの下のSTARTは, それぞれの節の先頭の位置; SIZEは節にあるリテラルの個数である.

Schemeで実装したプログラムは以下のようだ.

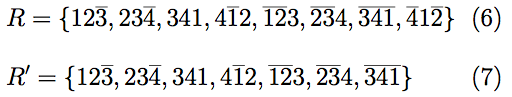
(define (algorithm7222a)
(define (and1 n) (if (even? n) 0 1))
;1とのandをとる
(define (xor1 n) ((if (even? n) + -) n 1))
;1とのxorをとる. リテラルの正負を反転する
(define (? b) (if b 1 0))
;iverson notation [b]=b?1:0

(define n 4) (define m 7)
(define ls '(0 0 0 0 0 0 0 0 0 0 9 7 3 8 7 5 6 5 3 8 4 3
 8 6 2 9 6 4 7 4 2))
(define fs '(0 0 30 21 29 17 26 28 22 25 9 7 3 8 11 5 6 15 12
 13 4 18 19 16 2 10 23 20 14 27 24))
(define bs '(0 0 24 12 20 15 16 11 13 10 25 14 18 19 28 17 23
 5 21 22 27 3 8 26 30 9 6 29 7 4 2))
(define cs '(0 0 2 3 3 2 3 3 3 2 7 7 7 6 6 6 5 5 5 4 4 4
 3 3 3 2 2 2 1 1 1))
(define size '(0 3 3 3 3 3 3 3))
(define start '(0 28 25 22 19 16 13 10))

(define ms (map (lambda (x) 0) (a2b 0 (+ n 1))))

(define l 0) (define a 0) (define d 0) (define p 0) 
(define i 0) (define j 0) (define q 0) (define r 0) 
(define s 0)

(call-with-current-continuation
 (lambda (exit)

(define (a1)
 (set! a m) (set! d 1)
 (a2))
(define (a2)
 (set! l (* 2 d))
 (if (<= (list-ref cs l) (list-ref cs (+ l 1)))
  (set! l (+ l 1)))
 (list-set! ms d (+ (and1 l) 
  (* 4 (? (= (list-ref cs (xor1 l)) 0)))))
 (newline) (display (list 'ms (take (+ d 1) ms)))
 (if (= (list-ref cs l) a) (begin (newline)
  (do ((i 1 (+ i 1))) ((> i n)) 
   (display (and1 (xor1 (list-ref ms i)))))
  (exit 'satisfiable)))
 (a3))

(define (a3back)
 (if (>= p (+ n n 2)) (begin
  (set! j (list-ref cs p))
  (set! i (list-ref size j))
  (list-set! size j (+ i 1))
  (set! p (list-ref bs p))
  (a3back)) (a5)))

(define (a3loop)
 (if (>= p (+ n n 2)) (begin
 (set! j (list-ref cs p))
 (set! i (list-ref size j))
 (if (> i 1) (begin
   (list-set! size j (- i 1)) 
   (set! p (list-ref fs p)) (a3loop))
  (begin (set! p (list-ref bs p)) (a3back))))
(a4)))

(define (a3)
 (set! p (list-ref fs (xor1 l)))
 (a3loop))

(define (a4loop)
 (if (>= p (+ n n 2)) (begin
  (set! j (list-ref cs p))
  (set! i (list-ref start j))
  (set! p (list-ref fs p)) 
  (do ((s i (+ s 1))) ((= s (+ i (list-ref size j) -1)))
   (set! q (list-ref fs s))
   (set! r (list-ref bs s))
   (list-set! bs q r)
   (list-set! fs r q)
   (list-set! cs (list-ref ls s)
    (- (list-ref cs (list-ref ls s)) 1)))
  (a4loop))))

(define (a4)
 (set! p (list-ref fs l))
 (a4loop)
 (set! a (- a (list-ref cs l))) (set! d (+ d 1)) 
 (a2))

(define (a5)
 (if (< (list-ref ms d) 2) (begin 
  (list-set! ms d (- 3 (list-ref ms d)))
  (set! l (+ (* 2 d) (and1 (list-ref ms d)))) (a3))
 (a6)))

(define (a6)
 (if (= d 1) (exit "unsatisfiable")
  (begin (set! d (- d 1))
   (set! l (+ (* 2 d) (and1 (list-ref ms d)))) (a7))))

(define (a7loop)
 (if (>= p (+ n n 2)) (begin
  (set! j (list-ref cs p))
  (set! i (list-ref start j))
  (set! p (list-ref bs p))
  (do ((s i (+ s 1))) ((= s (+ i (list-ref size j) -1)))
   (set! q (list-ref fs s))
   (set! r (list-ref bs s))
   (list-set! bs q s)
   (list-set! fs r s)
   (list-set! cs (list-ref ls s)
    (+ (list-ref cs (list-ref ls s)) 1)))
 (a7loop))))

(define (a7)
 (set! a (+ a (list-ref cs l)))
 (set! p (list-ref bs l))
 (a7loop)
 (a8))

(define (a8loop)
 (if (>= p (+ n n 2)) (begin
  (set! j (list-ref cs p))
  (set! i (list-ref size j))
  (list-set! size j (+ i 1))
  (set! p (list-ref fs p))
  (a8loop))))

(define (a8)
 (set! p (list-ref fs (xor1 l)))
 (a8loop)
 (a5))

(a1)))
)
(algorithm7222a)

途中, ステップA2で動作状況を示すmsを印字しながらの実行結果は

(ms (0 1))
(ms (0 1 0))
(ms (0 1 0 1))
(ms (0 1 0 1 4))
0101
;... done
;Value: satisfiable

で, 解はx₁=0, x₂=1, x₃=0, x₄=1 である.

TAOCPには(6)の実行中のmsの値も掲載してあるから

(define n 4) (define m 8)
(define ls '(0 0 0 0 0 0 0 0 0 0 9 5 2 9 7 3 8 7 5 6 5 3 8 4
 3 8 6 2 9 6 4 7 4 2))
(define fs '(0 0 33 24 32 20 29 31 25 28 9 5 2 10 7 3 8 14 11
 6 18 15 16 4 21 22 19 12 13 26 23 17 30 27))
(define bs '(0 0 12 15 23 11 19 14 16 10 13 18 27 28 17 21 22
 31 20 26 5 24 25 30 3 8 29 33 9 6 32 7 4 2))
(define cs '(0 0 3 3 3 3 3 3 3 3 8 8 8 7 7 7 6 6 6 5 5 5 4 4
 4 3 3 3 2 2 2 1 1 1))
(define size '(0 3 3 3 3 3 3 3 3))
(define start '(0 31 28 25 22 19 16 13 10))

として(6)もやってみると

(ms (0 1))
(ms (0 1 1))
(ms (0 1 1 0))
(ms (0 1 1 3 1))
(ms (0 1 2 1))
(ms (0 1 2 1 1))
(ms (0 1 2 2 1))
(ms (0 2 1))
(ms (0 2 1 1))
(ms (0 2 1 1 1))
(ms (0 2 1 2 1))
(ms (0 2 2 1))
(ms (0 2 2 2 1))
;... done
;Value 11: "unsatisfiable"

のように, TAOCPにあるのと同様な出力が得られた. まぁこの実装は間違ってはいないようだ.

SATソルバ

TAOCP 7.2.2.2は充足可能性(Satisfiability)が話題だ. 最初の方に多くの問題が CNF(Conjunctive Normal Form 乗法標準形)で記述できるという話が続く. 私はこの分野にはさほど興味がなく, まったくのど素人で, いつものようにアルゴリズ ムにだけ関心がある. 繰り返すまでもなく, TAOCPのアルゴリズムは自然言語で 記述されているから, その英文解釈が煩わしく, いつもああでもない, こうでもない と思いつつSchemeに変換し, いくつかの例題が無事に解けるのをみてやっと 安心している.

今回もそういう話である.

早速例をTAOCPから拝借すると, 乗法標準形は次のようなものである.


x₁, x₂, ...などが変数(variable). 変数または その上に線を引いたものがリテラル(literal). リテラルを∨でつないだものが 論理和節(clause), そしてCNFはそれらの節を∧でつないだものである.

かっこや∧や∨をいちいち書くのも面倒だということで, TAOCPではこれを


のように書いた.

さてSATソルバはFが真になるように, これらの変数に真(1), 偽(0)を対応させる もので, この例のサイズなら目の子で探せば解が見つかるが, 実用になる問題では 変数の個数がすごく多く, 高速なアルゴリズムが研究対象になっているらしい. ( 4月23日のブログMcGregorグラフを解く場合は440変数の1406論理和節になるとか.)

TAOCPにはまず基本的なアルゴリズムが出ていたので, 練習としてそれを Schemeで実装してみた.

まず上のCNFの例は, 私の実装ではS式で((1+ 2-) (2+ 3+) (1- 3-) (1- 2- 3+)) と書くことにする. 負のリテラルに-がつくだけでなく, 正のリテラルに+が つくのは対称性からきれいではないか. Schemeでは+1は数だが, 1+はシンボルになる. 従って 1+を1-にしたり, その逆にしたりは

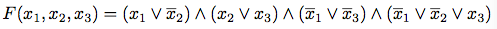
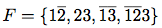
(define (neg l)
(let* ((s (symbol->string l)) (w (- (string-length s) 1)))
 (string-set! s w (integer->char 
  (- 88 (char->integer (string-ref s w)))))
 (string->symbol s)))

つまりリテラルlを貰い, その文字列sとその長さ-1のwを 作る. 最後の+か-を取り出し, ASCIIの値とし,

(char->integer #\+) => 43
(char->integer #\-) => 45

だからその和の88から引くと+, -が逆転できる. ついでだが, 変数の記号からリテラルを作る(例えば x からx+, x-, 2 から2+, 2-を作る)手続きは次のようだ.

 (define (lit v s)
  (string->symbol (string-append
   ((if (number? v) number->string symbol->string) v)
   (symbol->string s))))
(lit 'x '+) => x+
(lit 'x '-) => x-
(lit 2 '+) => 2+
(lit 2 '-) => 2-

TAOCPにあるSATソルバの基本的なアルゴリズムB(F)(7222-56)は次のようだ.





考えてみると, このアルゴリズムは当然と思える. Fは節がandで繋がってい るから, 空のandは真だ. (and) => #t.

andで繋がっている節に空のものがあると, 空の節は(or) => #f だから Fは偽になる.

そのどちらでもないなら, まだFに残っている変数の正と偽のリテラル を作り, それで「ただし」以下のF|lを用意してBに 再帰的に作用させ, その結果にリテラルを足したのを返す.

「ただし」の内容はこうだ. lを含む節は真なので, andの並びでは 考慮する必要がないから削除する. 一方lの否定を含む節はorに 偽の項は関係ないから項を削除する. いずれにしろlの変数は 消えることになる.

そうだと思って書いたのが次のSchemeのプログラムである.

(define (b f vs)
 (define (lit v s)
  (string->symbol (string-append
   ((if (number? v) number->string symbol->string) v)
   (symbol->string s))))
 (let ((a '()))
  (define (b1 f ls vs)
   (display (list 'b1 f ls vs )) (newline)
   (cond ((member '() f) #f)
         ((= (length (nub f)) 1)
          (set! a (cons (cons (caar f) ls) a)))
         (else
         (let ((l (lit (car vs) '+)))
           (b1 (apb f l) (cons l ls) (cdr vs)))
         (let ((l (lit (car vs) '-)))
           (b1 (apb f l) (cons l ls) (cdr vs))))))
 (b1 f '() vs) a))

引数のvsは変数のリストである.

だから上の例では

(b '((1+ 2-) (2+ 3+) (1- 3-) (1- 2- 3+)) '(1 2 3))

と呼び出す. 内部手続きb1が途中経過を示すので, 出力は

(b1 ((2+ 3+) (3-) (2- 3+)) (1+) (2 3))
(b1 ((3-) (3+)) (2+ 1+) (3))
(b1 (()) (3+ 2+ 1+) ())
(b1 (()) (3- 2+ 1+) ())
(b1 ((3+) (3-)) (2- 1+) (3))
(b1 (()) (3+ 2- 1+) ())
(b1 (()) (3- 2- 1+) ())
(b1 ((2-) (2+ 3+)) (1-) (2 3))
(b1 (()) (2+ 1-) (3))
(b1 ((3+)) (2- 1-) (3))
=> ((3+ 2- 1-))

トレースの最初の行は, 後ろから見て残りの変数は2と3, リテラルは1+. 従って((1+ 2-) (2+ 3+) (1- 3-) (1- 2- 3+))の左端の項は1+があるから削除. 次は1+, 1-もないからそのまま, 次の2項は1-を削除. そして((2+ 3+) (3-) (2- 3+))を得る.

次の行はリテラルが2+. そこで(2+ 3+)は削除. (2- 3+)の 2-を削除. ((3-) (3+))が残る.

次. 変数3に対して3+, 3-をリテラルとしても()が得られ. εなので 充足不能になる. バックトラックして2-をリテラルにしても失敗.

改めて1-をリテラルにしてみたところ, fが空リストになり成功した.

原理的にはこれでよいが, 実用的には工夫があるらしい. そういう改良 アルゴリズムの話がTAOCPでは続く. その説明はまたいずれ.