6月15日のブログで, 階差による計算法を書いた時, y=x2+x+41を例に使った. もちろんこれはEulerが1777年に見つけた素数の式である. (xが0から39までに対してyは素数になる. x=40の時は, 402+40+40+12=(40+1)2となり, 素数ではない.)
最近入手した, IEEE Annals of the History of Computing (Vol.31, No.2, April-June 2009)に, Prototype Fragments from Babbage's First Difference Engineという記事があった. 1822年頃, Babbageは階差機関を開発していた. 結局これは, 複製が上野の科学博物館などに展示されている, 職人のJoseph Clementの作った加算器の模型だけが出来たようにいわれている.
それでも見栄えは結構いいので, 情報処理学会の論文賞のメダルなどには, この加算器がレリーフになっている.
その後, 階差機関No.2は, Babbage生誕200年記念で作られ, ロンドンの科学博物館と, カリフォルニアのComputer History Museumで展示されている.
ところで, 上述の記事によると, この加算器以外に, 加算器用に作られた部品が, あちこちの博物館に保存されているということである. 真偽いろいろあるらしく, 試作品のものなど, 怪しいものもあるらしい. そういうものを集める博物館も博物館だが, それを調べる人も調べる人だ.
実は, 私の気になったのは, 記事に引用されているBabbageによる解説である. 1822 年7月3 日に, BabbageがSir Humphry Davyに送った手紙の一節が示されており, 「it proceeded to make a table from the formula x2+x+41.」と書いてあるのだ.
Eulerが発見してから, 半世紀も経っているので, Babbageもこの式を知っていたのであろう. やはりこれは特別な式なのだ.
2009年7月29日水曜日
2009年7月25日土曜日
長大語計算
TAOCPにbroadword computingという話題がある. 長大なビット列に対する演算法である.
例えば x=1110111101100111 の中で 0111 というパターンを探す問題である.
その答は q=0001000000001000 である. つまりqの1に対応するxの場所が0111の0であり, その右に111があるのだ.
方法は q=¬x & x<<1 & x<<2 & x<<3 とすればよい. 途中の状況を示すと下のようだ.
つまり探すパターンの各ビットが0なら¬x, 1ならxのままを, 左シフトで, 答の位置に集め, 全体の&をとれば得られるわけである.
応用問題として, 5月8日のブログの最初にあるQ0とQ1から11011, つまり双子の素数が並んでいる場所を探してみる.
として, x & x<<1 & (¬x)<<2 & x<<3 & x<<4 で良い筈である.
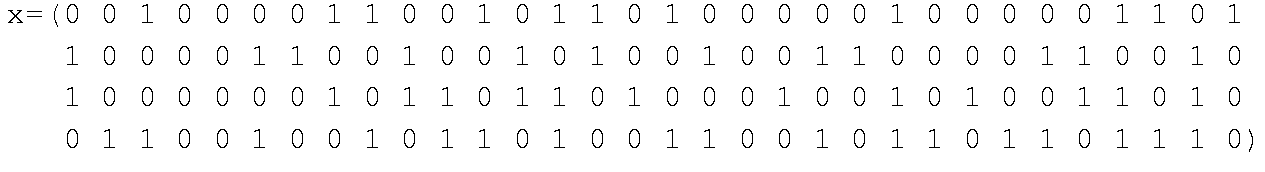
から
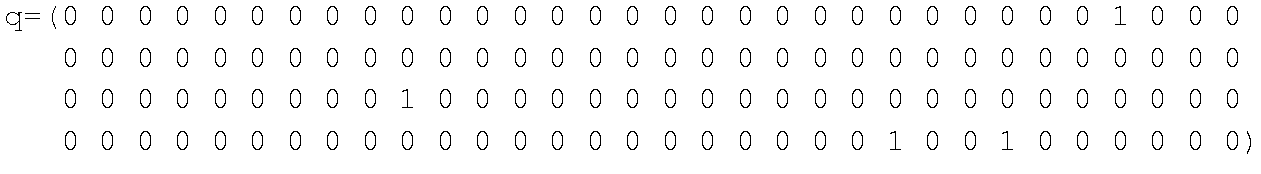
が得られる. つまり, 5と7と11と13, 11と13と17と19で, この辺はすぐ思いつく. その次は101と103と107と109であり, さらに191と193と197と199が続く. これだけ素数が連続するから, 他の小さい素数はどこに隠れるか見てみると
のように, 7, 13, 17がうまく2や5と一緒になる.
も同様.
ついでにQ0からQ7までを使い

として, もう少し先まで探すと qが得られ, 最左の1の位置を求める.
(ここでi2bは整数を0と1のビット列にする関数. iandなどは, 2つの整数のビット毎ANDなど, ilshは整数のビット左シフトである.)
従って並ぶ双子の最大の素数は
であり, この辺りは
次は
となり, 先ほどの199, 197, 193, 191が得られる.
例えば x=1110111101100111 の中で 0111 というパターンを探す問題である.
その答は q=0001000000001000 である. つまりqの1に対応するxの場所が0111の0であり, その右に111があるのだ.
方法は q=¬x & x<<1 & x<<2 & x<<3 とすればよい. 途中の状況を示すと下のようだ.
x =(1 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1)
¬ x =(0 0 0 1 0 0 0 0 1 0 0 1 1 0 0 0)
x<<1 =(1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 0)
x<<2 =(1 0 1 1 1 1 0 1 1 0 0 1 1 1 0 0)
x<<3 =(0 1 1 1 1 0 1 1 0 0 1 1 1 0 0 0)
q =(0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0)
つまり探すパターンの各ビットが0なら¬x, 1ならxのままを, 左シフトで, 答の位置に集め, 全体の&をとれば得られるわけである.
応用問題として, 5月8日のブログの最初にあるQ0とQ1から11011, つまり双子の素数が並んでいる場所を探してみる.
(define x #x2196820D864A4C32816D129A64B4CB6E)
として, x & x<<1 & (¬x)<<2 & x<<3 & x<<4 で良い筈である.
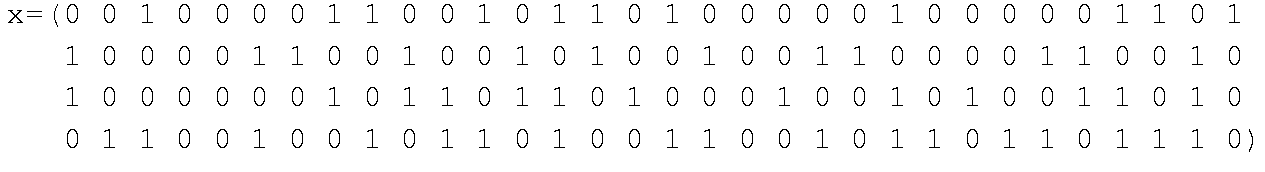
から
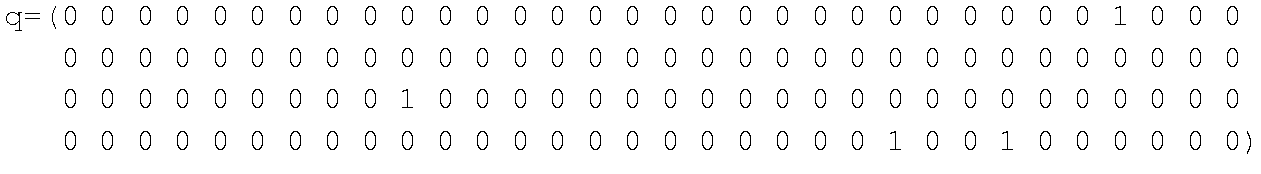
が得られる. つまり, 5と7と11と13, 11と13と17と19で, この辺はすぐ思いつく. その次は101と103と107と109であり, さらに191と193と197と199が続く. これだけ素数が連続するから, 他の小さい素数はどこに隠れるか見てみると
101 = 101
102 = 17 3 2
103 = 103
104 = 13 2 2 2
105 = 7 5 3
106 = 53 2
107 = 107
108 = 3 3 3 2 2
109 = 109
のように, 7, 13, 17がうまく2や5と一緒になる.
191 = 191
192 = 3 2 2 2 2 2 2
193 = 193
194 = 97 2
195 = 13 5 3
196 = 7 7 2 2
197 = 197
198 = 11 3 3 2
199 = 199
も同様.
ついでにQ0からQ7までを使い

として, もう少し先まで探すと qが得られ, 最左の1の位置を求める.
(ここでi2bは整数を0と1のビット列にする関数. iandなどは, 2つの整数のビット毎ANDなど, ilshは整数のビット左シフトである.)
(length (member 1 q)) => 940
従って並ぶ双子の最大の素数は
(- (* 940 2) 1) => 1879
であり, この辺りは
1871 = 1871
1872 = 13 3 3 2 2 2 2
1873 = 1873
1874 = 937 2
1875 = 5 5 5 5 3
1876 = 67 7 2 2
1877 = 1877
1878 = 313 3 2
1879 = 1879
次は
(length (member 1 (list-tail q (- 1024 940 -1)))) => 745
(- (* 745 2) 1)) => 1489
1481 = 1481
1482 = 19 13 3 2
1483 = 1483
1484 = 53 7 2 2
1485 = 11 5 3 3 3
1486 = 743 2
1487 = 1487
1488 = 31 3 2 2 2 2
1489 = 1489
(length (member 1 (list-tail q (- 1024 745 -1)))) => 415
(- (* 415 2) 1) => 829
821 = 821
822 = 137 3 2
823 = 823
824 = 103 2 2 2
825 = 11 5 5 3
826 = 59 7 2
827 = 827
828 = 23 3 3 2 2
829 = 829
(length (member 1 (list-tail q (- 1024 415 -1)))) => 100
となり, 先ほどの199, 197, 193, 191が得られる.
2009年7月2日木曜日
手回し機械式計算機
6月15日のブログで触れたComrieの論文には, Duplaを使った第2階差をとる方法が書いてある. それは次のようだ.
等間隔の引数に対する関数値が, a, b, c, d, ...だったとする.
第1階差は, b-a, c-b, d-c, ...だから,
第2階差は(c-b)-(b-a)=a-2b+c, (d-c)-(c-b)=b-2c+d, ... である.
この種の計算機では, 数値を入力するのが厄介(というより, 操作ミスの原因)なので, 入力回数を極力少なくするのに気を使った. 以下の方法では, 「なにを置く」は, 各値について1回だけだ. 第2階差は「記録」のところで得られる.
この「cを置く」から, 「dを置く」の直前までが1サイクルである. ここから, R1とR2の仕事を交換し, R2に次の階差が得られる. 以下同じ.
実に見事な方法だ. 次の入力数を置数レジスタに置いたまま, 2つのレジスタを使い, 次の階差と次の次の階差の準備を進めている. Duplaでは, 一方に足しながら, 他方から引くことも出来るが, そのようにしていないのは, 操作ミスを心配したからと思われる.
これは今の言葉でいえば, プログラムを作ったようなものである. 手順を書き下し, 後はこの通りに手を動かすだけでよい. 最初に書いたように, それぞれの値が1回しか, 入力されないのが, 最大のメリットである.
Leslie John Comrie(1893-1950)は, 化学を専攻したが, 後に天文学者になり, 各種の計算機を使って数表を作る仕事に尽力した. 計算機も単に手回し機にとどまらず, パンチカードを使った会計機等も利用した. 「A Computer Perspective計算機創造の歴史」には, Comrieは何回も登場する.
Comrieの写真はここにある.
等間隔の引数に対する関数値が, a, b, c, d, ...だったとする.
第1階差は, b-a, c-b, d-c, ...だから,
第2階差は(c-b)-(b-a)=a-2b+c, (d-c)-(c-b)=b-2c+d, ... である.
この種の計算機では, 数値を入力するのが厄介(というより, 操作ミスの原因)なので, 入力回数を極力少なくするのに気を使った. 以下の方法では, 「なにを置く」は, 各値について1回だけだ. 第2階差は「記録」のところで得られる.
S R1 R2
aを置く a 0 0
1回転 a a a
bを置く b a a
-3回転 b a-3b a-3b
R2帰零 b a-3b 0
1回転 b a-2b b
1 cを置く c a-2b b
2 1回転 c a-2b+c b+c
3 記録 c 階差 b+c
4 -4回転 c a-2b-3c b-3c
5 R1帰零 c 0 b-3c
6 1回転 c c b-2c
1 dを置く d c b-2c
...
この「cを置く」から, 「dを置く」の直前までが1サイクルである. ここから, R1とR2の仕事を交換し, R2に次の階差が得られる. 以下同じ.
実に見事な方法だ. 次の入力数を置数レジスタに置いたまま, 2つのレジスタを使い, 次の階差と次の次の階差の準備を進めている. Duplaでは, 一方に足しながら, 他方から引くことも出来るが, そのようにしていないのは, 操作ミスを心配したからと思われる.
これは今の言葉でいえば, プログラムを作ったようなものである. 手順を書き下し, 後はこの通りに手を動かすだけでよい. 最初に書いたように, それぞれの値が1回しか, 入力されないのが, 最大のメリットである.
Leslie John Comrie(1893-1950)は, 化学を専攻したが, 後に天文学者になり, 各種の計算機を使って数表を作る仕事に尽力した. 計算機も単に手回し機にとどまらず, パンチカードを使った会計機等も利用した. 「A Computer Perspective計算機創造の歴史」には, Comrieは何回も登場する.
Comrieの写真はここにある.
2009年7月1日水曜日
再帰曲線
6月23日のblogの続き, 演習問題の解答である.
下の図の a は1枚の紙を上から見たところで, 一度も折らない, つまり0次のdragon曲線を表わす. dragon曲線には始点と終点を考える. 始点から終点へ向う矢印で, dragon曲線を表わすとすると, a は b のようになる. 矢印の先端の0は, 0次を意味する.
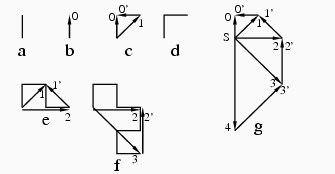
dragon曲線は紙を半分に折り, 折り目を直角に開くのだが, それの相当するのは, dragon曲線を表わす矢印の先に, 同じ矢印を右から合わせることである. 従って1次のdragon曲線の矢印1は, 0次の矢印0と矢印0' から c のように作れる. 対応する1次のdragon曲線はd.
2次のdragon曲線と矢印の図をeに示す. 次はfのようだ.
このようにして, dragon曲線を次々と描くと, gの図が出来る. sは共通の始点である.
次にこれを青竜と赤竜で描いてみる.
aは0次の竜をつなげたもの. 青の始点は下, 終点は上で, 赤の始点は上, 終点は下である.
bは1次の青竜の終点に1次の赤竜の始点, 青竜の始点に赤竜の終点をつなげた.
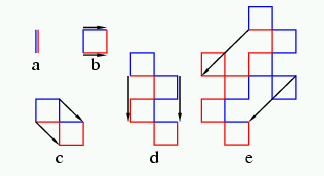
0次の青を終点から1次の青の終点への上の矢印と1次の赤の終点から0次の赤の終点への下の矢印も示す. この矢印は, 前のblogの用語でいえば, 新興勢力がどこに出来たを示す.
このようにして, c, d, eはそれぞれ, 1次から2次, 2次から3次, 3次から4次へ新興勢力が拡大していく様子を示す.
これで分かるのは, 新版図は, 方向は45度ずつ時計回りにまわり, 距離は√2倍ずつ増えていることである.
一方, 例のフラクタル図の方は, 新版図は135度, 反時計回りにまわり, 距離は√2倍になっていたので, 結局同じように増殖していたことが判明した.
詳しくは, 竜の図で, 拡大したときにぶつからないことなど, 確認する必要があるが, 大体は良さそうに思った.
下の図の a は1枚の紙を上から見たところで, 一度も折らない, つまり0次のdragon曲線を表わす. dragon曲線には始点と終点を考える. 始点から終点へ向う矢印で, dragon曲線を表わすとすると, a は b のようになる. 矢印の先端の0は, 0次を意味する.

dragon曲線は紙を半分に折り, 折り目を直角に開くのだが, それの相当するのは, dragon曲線を表わす矢印の先に, 同じ矢印を右から合わせることである. 従って1次のdragon曲線の矢印1は, 0次の矢印0と矢印0' から c のように作れる. 対応する1次のdragon曲線はd.
2次のdragon曲線と矢印の図をeに示す. 次はfのようだ.
このようにして, dragon曲線を次々と描くと, gの図が出来る. sは共通の始点である.
次にこれを青竜と赤竜で描いてみる.
aは0次の竜をつなげたもの. 青の始点は下, 終点は上で, 赤の始点は上, 終点は下である.
bは1次の青竜の終点に1次の赤竜の始点, 青竜の始点に赤竜の終点をつなげた.

0次の青を終点から1次の青の終点への上の矢印と1次の赤の終点から0次の赤の終点への下の矢印も示す. この矢印は, 前のblogの用語でいえば, 新興勢力がどこに出来たを示す.
このようにして, c, d, eはそれぞれ, 1次から2次, 2次から3次, 3次から4次へ新興勢力が拡大していく様子を示す.
これで分かるのは, 新版図は, 方向は45度ずつ時計回りにまわり, 距離は√2倍ずつ増えていることである.
一方, 例のフラクタル図の方は, 新版図は135度, 反時計回りにまわり, 距離は√2倍になっていたので, 結局同じように増殖していたことが判明した.
詳しくは, 竜の図で, 拡大したときにぶつからないことなど, 確認する必要があるが, 大体は良さそうに思った.
登録:
投稿 (Atom)
