なんとか数にはFibonacci数, Mersenne数, Goedel数, Meertens数, Erdos数など, 数々あるが, Ulam数はあまりポピュラーではないようで, 私は始めて聞いた. A New Kind of Scienceにはちゃんとあった.
こういう数列である.
<U1, U2,...>=
<1,2,3,4,6,8,11,13,16,18,26,28,36,38,47,48,53,57,62,69,72,77,82,87,97,99,...>
で, U1=1, U2=2, Un(n≥3)は, 0<j<k<n(jとkは違う)のUj+Ukの一通りの和で >Un-1の最小のものという定義である.
U3は, >U2だからまず3が候補で, 3=U1+U2が1通りなので, 3である.
U4は, >U3だからまず4が候補で, 同じU2を使う2+2は許されないが, 4=U1+U3が1通りなので, 4である.
U5は, >U4だからまず5が候補だが, 5は1+4と2+3と2通りで出来るので失格. 6は2+4しかないのでU5=6となる.
U6は, 6の次の7が候補だが, 7は1+6と3+4と2通りで出来るので失格し, 3+5=8になる.
こういう計算をするプログラムをSchemeで正直に書いて実行してみると, Fibonacci数以上に再帰が起き, U10くらいで辛抱出来なくなる.
上の数列は, SICPにあるメモ化に書き直して計算したものである. もちろんメモ化で断然速くなる.
演習問題の趣旨は, これをビット計算で高速化せよというものだ. もともとはBITの論文にあるらしいが, 解答を見ると以下のようになっている.
今回のブログは, このアルゴリズムの謎解きである.
aとbの2つのビット列を使う. nとm=Unまで計算が進んだとき, 0≤s<2mのsについて, aのs番目のビットの意味は, [s=1であるかs=2であるかsは<mの異なるUlam数の1通りの和かである]. bのs番目のビットの意味は, [sは<mの異なるUlam数の2通り以上の和である]である. ただし[述語]は述語が真の時1, 偽の時0とする(Iverson記法).
従ってn=2, m=U2=2の時, a=0111(左から順に, s=0だから上の述語に合わず0; s=1だから1; s=2だから1, s=3はU1+U2の1通りだから1). b=0000(どのsも2通り以上の和にならない)
さてn←n+1の時のアルゴリズムは次のようだ.
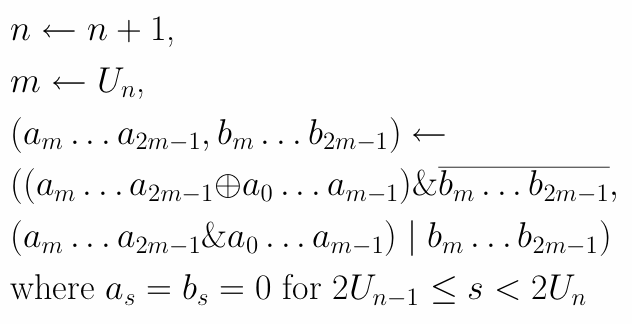
実際aとbは次のようになる.
n=3, mはam+1から右へ探して最初の1の添字, つまり0111の1番右のa3から探し始めると, いきなり1だからm=3. これがU(n=)3=3である. Un-1=2, Un=3だから, アルゴリズムの但し書き(where以下)に従い, a4...a5は0, またb4...b5は0だから, a, bは4ビットから6ビットになり, a=011100, b=000000にする. aを0から2までと3から5までに分け, bは3から5を使う.
アルゴリズムでは代入の左辺が(am...a2m-1,bm...b2m-1)のように書いてあるが, これは右辺を計算してからam...a2m-1とbm...b2m-1に代入したいという気持である. つまり
新しいaの3から5は, (100⊕011)&¬000=111.
新しいbの3から5は, (100&011)|000=000.
従ってa=011111, b=000000になる.
次はn=4, m=(a4から右へ探すので)4. 但し書きによりa=01111100, b=00000000になり, aの4から7は (1100⊕0111)&¬0000=1011. bの4から7は(1100&0111)|0000=0100. 従ってa=01111011, b=00000100.
では, これはなにをやったか.
a=011100の時, U1,U2,U3は1通りの和で作れるということであった. aの3から5は100だったが, まずU3の1はこれが1通りの和であることを示す. それにaの0から2の011をxorするのは, 左からの位置sはm+sの和で作れることを示す. 3については3+0はない; 4については3+1がある; 5については3+2があるということだ. すでに1通りで出来るものは, xorでその条件がリセットされてしまう.
一方, bm+sはリセットされる時はasとam+sが共に1なので1になり, つまり2通りで和が作れることを記憶する.
またaに戻り, その後, bs+mの否定とandをとるのは, 一度リセットされたら, あとは別の和で作れることが分かっても, 1に戻さないためである.
またbの方は, 前の値とorをとるから, 一旦2通り以上となれば, ずーっとこのビットは設定されたままになる.
かような次第で, このアルゴリズムを1回使うと, 次のUlam数が1つ得られる.
MIT Schemeにはbit-stringというデータ型があり, and, or, xor, not, stringappend, substringがとれ, またビットを探す関数もあるから, このアルゴリズムを書くのにお誂え向きである. ただしビットの番号は右端が0なので, 上の説明とは添字の向きが反対になる.
3から始め, c個のUlam数を計算するプログラムは以下の通り.
(define a (unsigned-integer->bit-string 4 14))
(define b (unsigned-integer->bit-string 4 0))
(define n 2) (define m 2)
(define (ulam c)
(if (> c 0) (let* ((m1) (z) (a1))
(set! n (+ n 1))
(set! m1 (bit-substring-find-next-set-bit
a (+ m 1) (* m 2)))
(display (list n m1)) (newline) ;nとmのリストを出力する.
(set! z (make-bit-string (* (- m1 m) 2) #f))
(set! a (bit-string-append a z))
(set! b (bit-string-append b z))
(set! m m1)
(set! a1 (bit-string-and
(bit-string-xor (bit-substring a 0 m)
(bit-substring a m (* m 2)))
(bit-string-not (bit-substring b m (* m 2)))))
(bit-substring-move-right! (bit-string-or
(bit-string-and (bit-substring a 0 m)
(bit-substring a m (* m 2)))
(bit-substring b m (* m 2))) 0 m b m)
(bit-substring-move-right! a1 0 m a m)
(ulam (- c 1))) 'ok))
実行結果は
(ulam 10)
(3 3)
(4 4)
(5 6)
(6 8)
(7 11)
(8 13)
(9 16)
(10 18)
(11 26)
(12 28)
=> ok
面白いよね.