順列の生成
n個の要素のすべての順列を生成するのも情報科学標準問題である.
私のSchemeのライブラリには
(define (permutation ls) ;list of permutation of ls
(define (list-del l n)
(if (= n 0) (cdr l)
(cons (car l) (list-del (cdr l) (- n 1)))))
(if (null? ls) '(())
(apply append (map (lambda (i)
(let ((x (list-ref ls i)))
(map (lambda (p) (cons x p))
(permutation (list-del ls i)) )))
(a2b 0 (length ls))))))
;(permutation '(a b c))=>
;((a b c) (a c b) (b a c) (b c a) (c a b) (c b a))
というのが置いてある. (list-del l n)はlのn番目の要素を取り去ったリストを返す. 本体は順列をとるリストが空なら空リストのリストを返す. そうでないなら最後の行(a2b 0 (length ls))でlsが(a b c)なら(0 1 2)のリストを作り, その各々を(lambda (i)..)のiとして(let..以下をやったものをappendする.
(let以下のxはlist-refだからa,b,cになり, それぞれlist-delした(b c) (a c) (a b)の順列の先頭に付ける. だから(a b c) (a c b) (b a c) (b c a) (c a b) (c b a)をappendすることになり, (a b c)の順列が完成する.
さてgpmには配列もリストもないから, また引数列を活用するプログラムを考えなければならない. 引数の長さに従って別のマクロを用意しなければならない.
そう考えて書いたのが次だ.
$def,p2,<~1~2~3>; $def,p3,<$p2,~1,~2,~3; $p2,~1,~3,~2;>; $def,p4,<$p3,~1~2,~3,~4; $p3,~1~3,~2,~4; $p3,~1~4,~2,~3;>; $def,p5,<$p4,~1~2,~3,~4,~5; $p4,~1~3,~2,~4,~5; $p4,~1~4,~2,~3,~5; $p4,~1~5,~2,~3,~4;>;これはまずp5を$p5,,a,b,c,d;のように呼ぶ. 第1引数が空, 第2引数以降がa,b,c,d である.
そこでp5の定義を見ると, $p4,空a,b,c,d;$p4,空b,a,c,d;$p4,空c,a,b,d;$p4,空d,a,b,c;とp4を呼び出している. つまりp4の第1引数は上のSchemeのプログラムのx, 以降はlist-delの結果に対応している.
p4の定義を見ると, $p3,~1~2,~3,~4;と呼ぶから, 最初のp4の呼出からは$p3,空ab,c,d;$p3,空ac,b,d;$p3,空ad,b,c;と呼出され, その最初のp3の呼出では$p2,空ab,c,d;$p2,空ab,d,c;と呼出され, p2によってabcd, abdcと出力される.
なんだか全部の順列を自分で書いたみたいな気もするが, これで完成である. 引数の数だけマクロを用意するのは面倒だが, それを我慢すれば存外簡単であった.
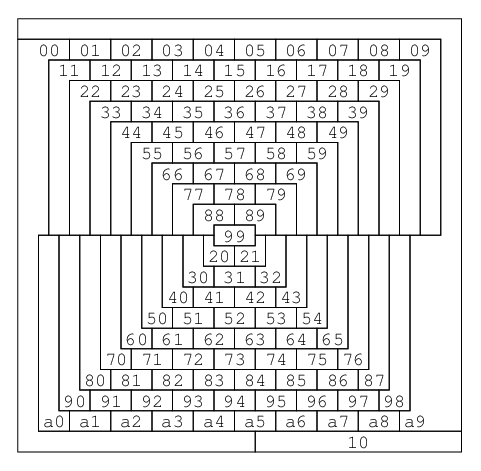
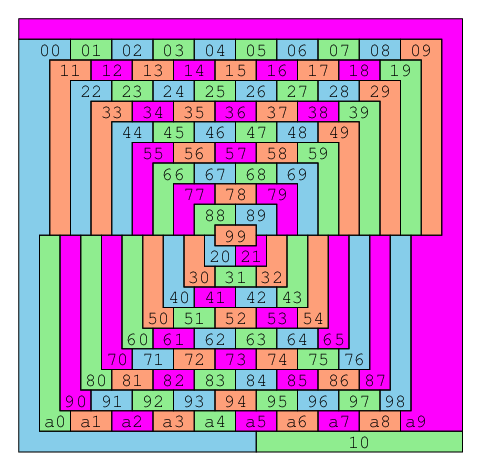
 であった. と書いた理由はTAOCPにひとつの色は7区画でしか使わない解があるという記述があったからだ. そういう解を探すのはまた大変そうだ.
であった. と書いた理由はTAOCPにひとつの色は7区画でしか使わない解があるという記述があったからだ. そういう解を探すのはまた大変そうだ.
