dragon曲線は, 紙を同じ向きに半分半分と折り, 折り目を90度になるように広げたものであった.
最近, この折る向きを毎回逆にしたらどうなるかと思った. 紙を折ってやってみるのは, やはり3,4回が限度であり, 手元の計算機の威力を借りたくなった.
下の図を見て欲しい.
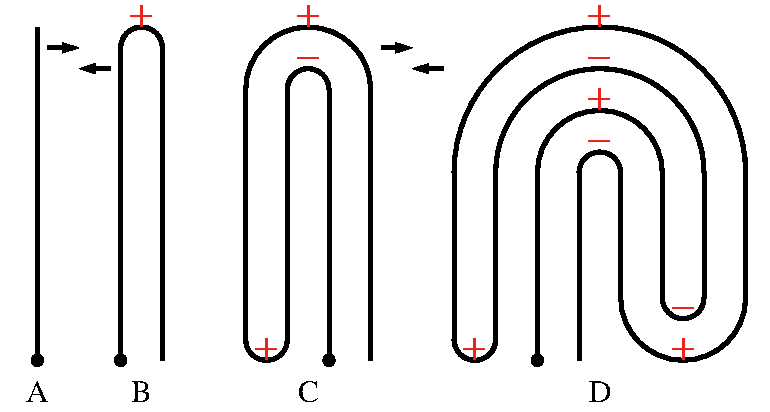
左端のAは折る前である. 下の黒丸は出発点を示す. その上の方に右向きの矢印が示すように, 最初は右に折る. するとBのようになる. 紙の長さが倍にになっているが, 今は折り方が問題なので, 分かりやすく描いてある.
出発点から途中右折したので, その角には+が付けてある.
Bを今度は左へ折る. 最初の折り目の+は左の下へ移動する. Cの出発点から辿ると, 最初は左折, 次がBで出来た右折, さらに右折する.
Cを次は右へ折るとDになる. 上の方の+や-は, 今回出来たのもで, 下の方のは左がCの下にあった折り目, 右がCの上にあったものだ.
出発点からの右折左折を抜き出すと
B +
C - + +
D + - - + + + -
この伝でつづけると次は
E - + + - - - + + - + + + - - +
となる.
一段上の列の要素を間に+と-を交互に入れたものになっているが, dragon曲線の場合と同じで, このパターンに着目する.
EをX3, DをX3とすると, X3の左半分はX2の+-を反対にしたものだ. 右半分は中央だけが違って右半分を殆んど同じである.
そこで, 'で+-の反転を表わすとすると,
X3=X2'+Y2'.
結局
X0=+, Y0=-,
Xn=Xn-1'+Yn-1',
Yn=Xn-1'-Yn-1'
となることが分かる.
Schemeでプログラムしてみる. この引数のnは上の漸化式の2n-1になっている.
(define (r s) (if (eq? s '+) '- '+))
(define (x n i) (cond ((= i n) '+)
((< i n) (r (x (/ n 2) i)))
((> i n) (r (y (/ n 2) (- i n))))))
(define (y n i) (cond ((= i n) '-)
((< i n) (r (x (/ n 2) i)))
((> i n) (r (y (/ n 2) (- i n))))))
(map (lambda (i) (x 8 i)) (a2b 1 16))
=> (- + + - - - + + - + + + - - +)
これで右折左折の情報が得られたから, いよいよ交互折りの曲線を描くことする.
そして出来たのが次の図である. X1からX8までが, 色を変えながら描いてある. 左中ほど上の, 直角に下の曲がった青の線がB(X1)である.
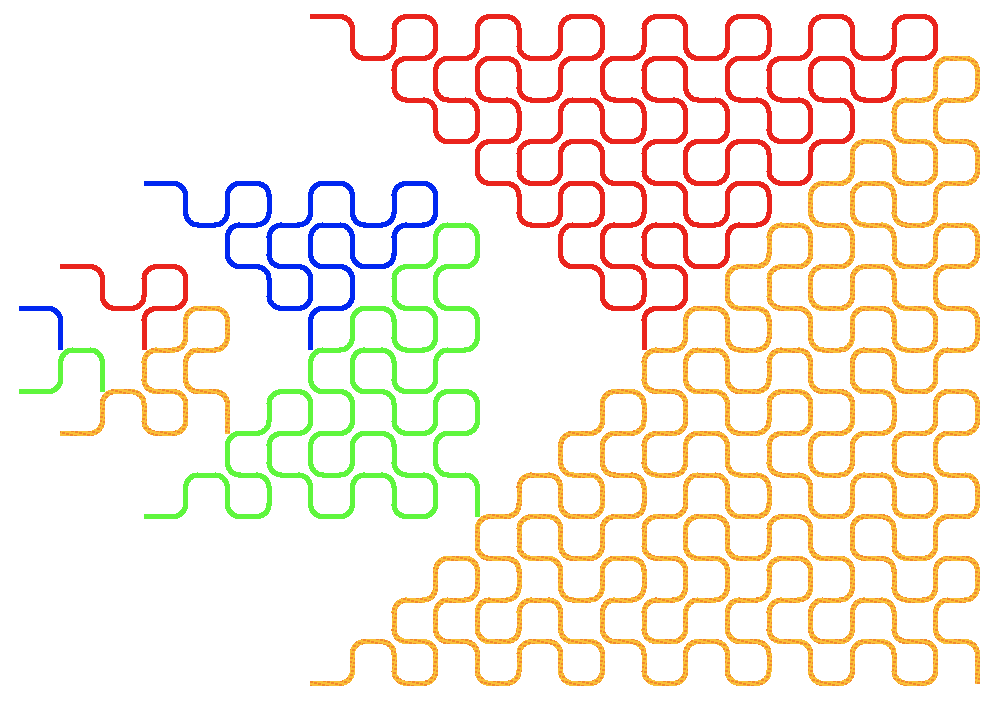
左から右向きに出発するのが, 出発点である. その下の緑の線がC(X2)に対応する.
折角描いてみたが, 竜にも鳳凰にもならず, 単に三角形が出来ただけであった. 思うにdragon曲線を考えた人も, これもやっては見たが, つまらない結果だったので, このことは書いて置かなかったのかもしれない.
つまらない絵しか描けないことが分かっただけでも, 一応の知見が得られたというべきか.




