The side of a regular hexagon is of length n (n is an integer). By equidistant parallels to its sides the hexagon is divided into T equilateral triangles each of which has sides of length 1. Let V denote the number of vertices appearing in this division, and L the number of boundary lines of length 1. (A boundary line belongs to one or two triangles, a vertex to two or more triangles.) When n = 1, which is the simplest case, T = 6, V = 7, L = 12. Consider the general case and express T, V, and L in terms of n. (Guessing is good, proving is better.)
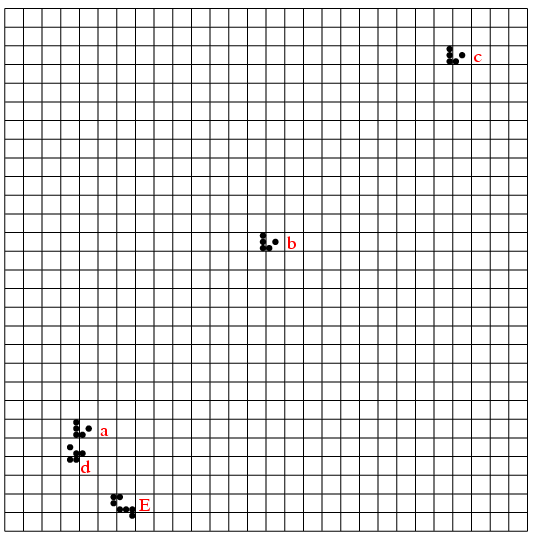
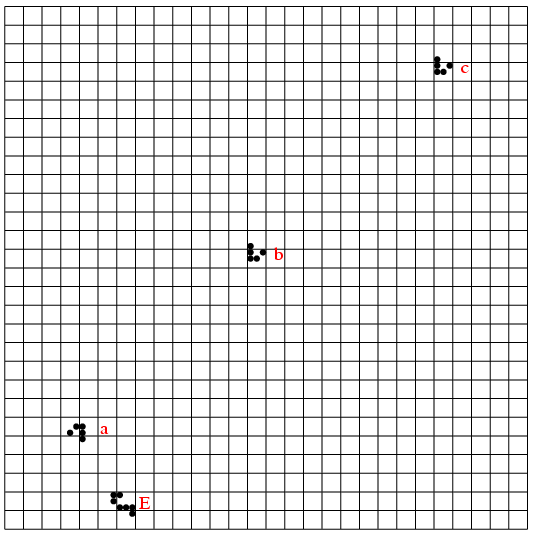
とりあえずn=1,2,3の絵を描いてみる。
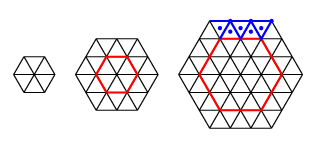
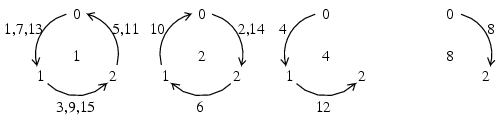
こういう図は, 幾何学と同じで正確に描くことが重要である. 幸いPostScriptで奇麗に描けた.
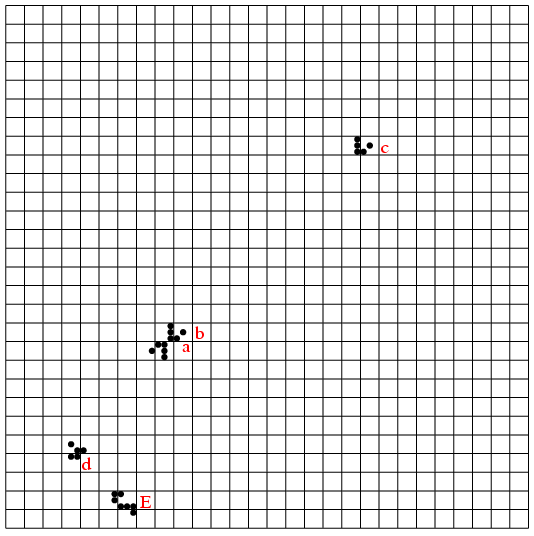
さて, 大きい図で全部数えるのは面倒だし, 間違えの元だ. うまい具合に中の方は赤で囲んだ左隣りと同じだから, 一番外の皮の部分だけに注目する. またそれも6回対称だから, 1/6だけ数えればよい.
n=3の図で数えると, T は5個増えた. n=2では3増えたから, ΔT(n)=2n -1であろう. 青い点をつけた頂点V は3増えたから, これはΔV(n)=nだ. Lは8だからΔL(n)=3n -1.
従って1辺がnの時の総和はn=0の時の値に, これらの式の6倍を, nを1からnまでの和にし, 定数はnを掛けて足せばよい.
だから
T(n) = 6·2n(n+1)/2-6n = 6n2+6n-6n = 6n2.
V(n) = 6n(n+1)/2+1 = 3n2+3n+1.
L(n)=6·3n(n+1)/2-6n = 9n2+9n-6n = 9n2+3n.
簡単すぎた. 食後の一休みにはちょうどよいかも. PostScriptの絵を描いたり, HTMLで式を書いたりで, 結構時間は掛かったが.