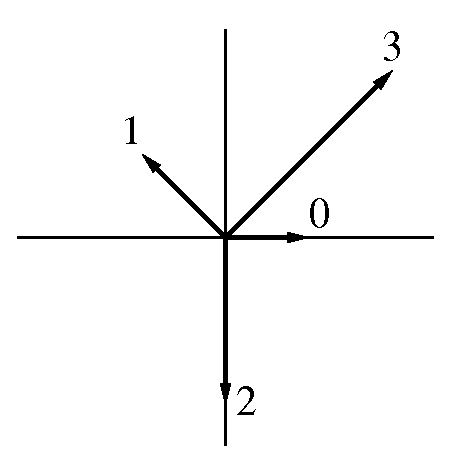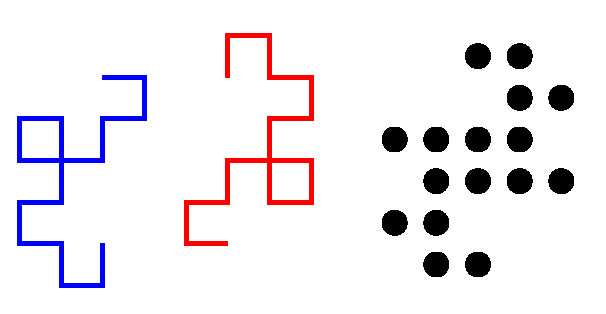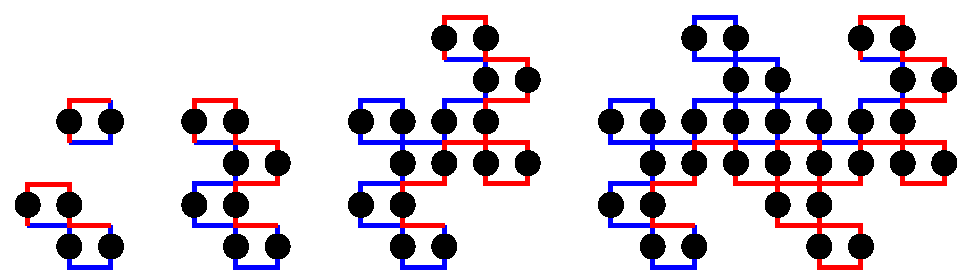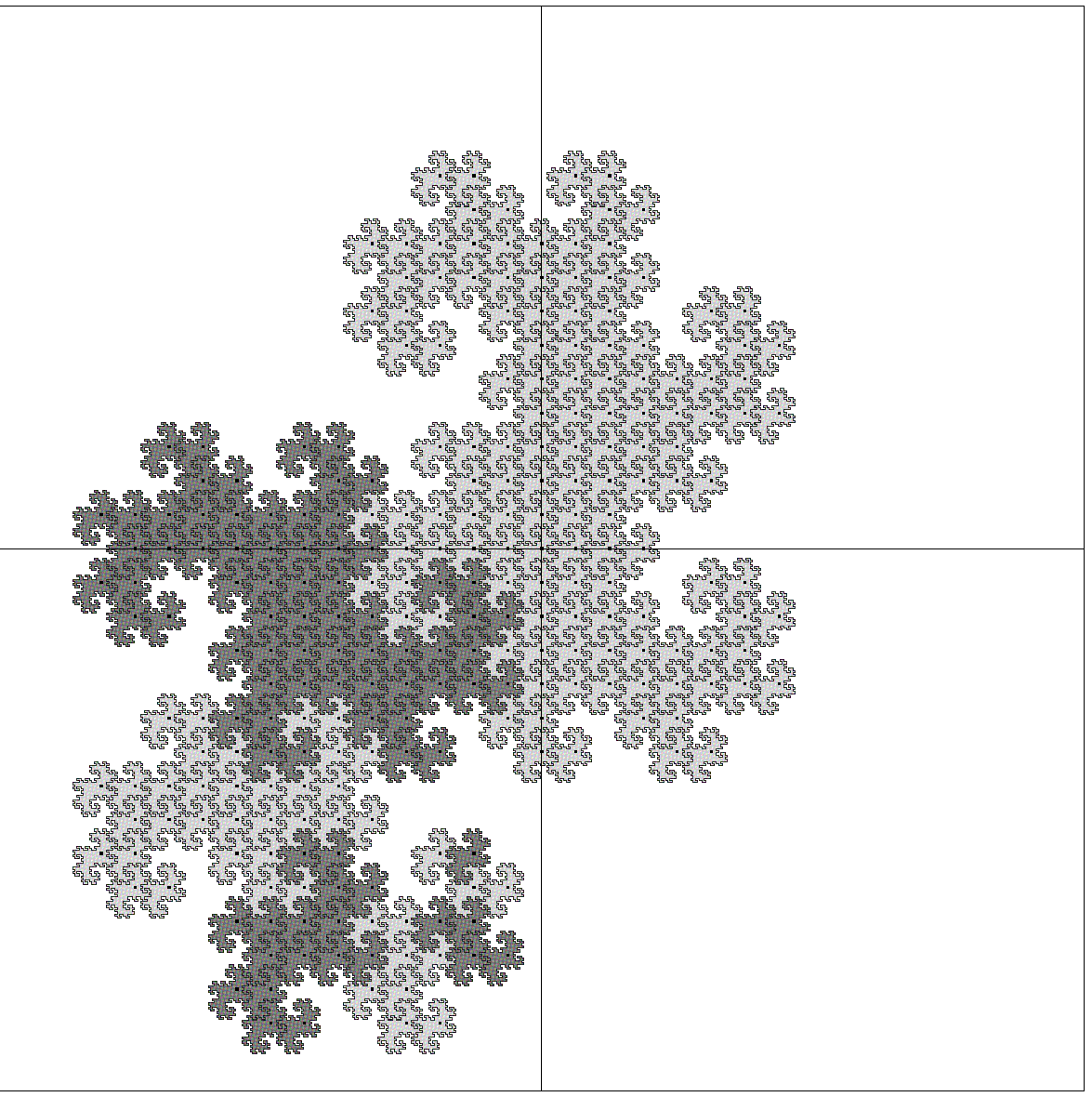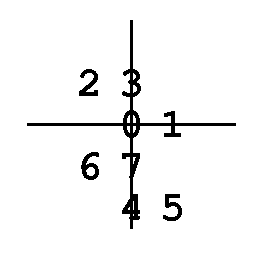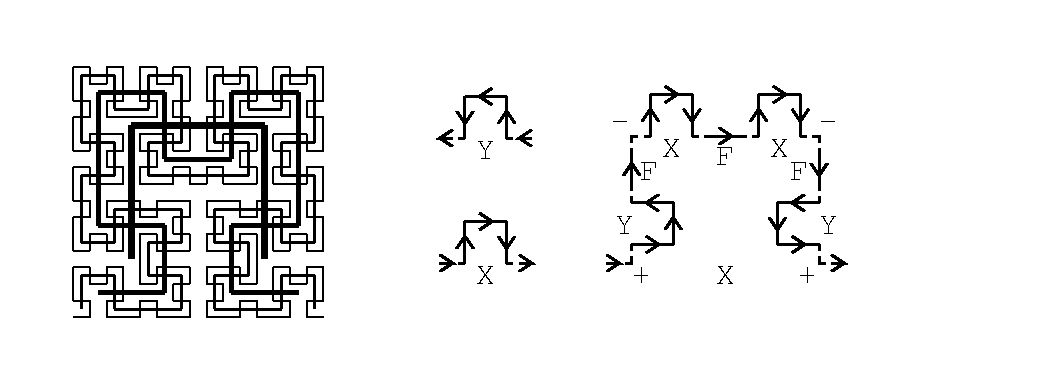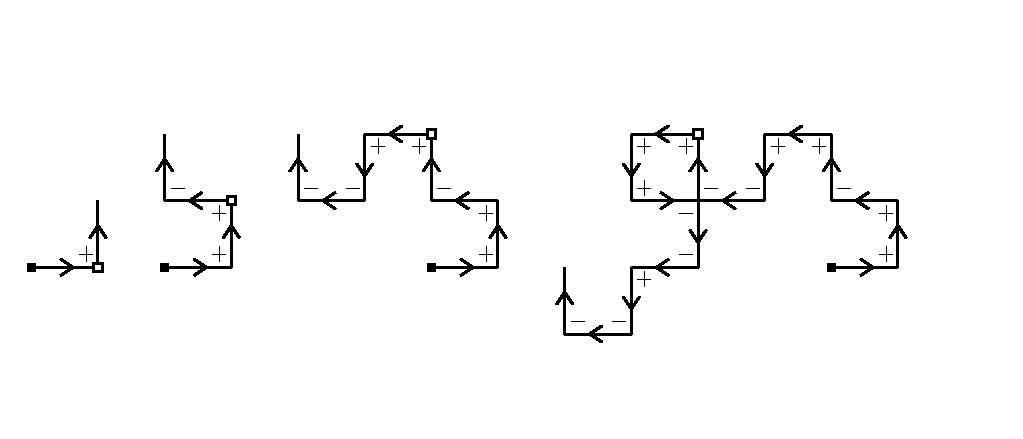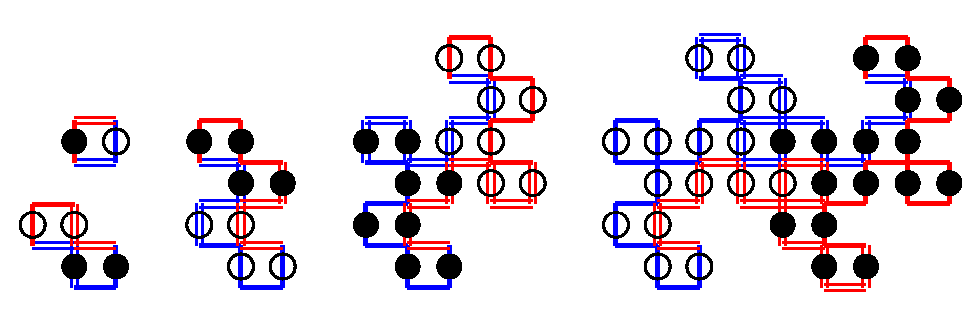
フラクタルの図には, 黒丸の他に白丸がある. dragon曲線では, 太線と2重線がある. 想像出来るように, 白丸は0, 1, 2,...と点をプロットした順で, 後半のものである. また2重線も, dragon曲線を順に描いた時の, 後半の線である. つまり白っぽいものは, いわば新興勢力である.
フラクタルの新興勢力は, i-1の冪乗の地域に発展する. それに対し, dragon曲線でも, 顕著な向きは分からぬまでも, 大雑把な方向は読める. すると左上の次数n=1から順に
n 赤の新勢力 青の新勢力 フラクタルの新勢力
1 右 左 右
2 右下 左上 左上
3 下 上 下
4 左下 右上 右上
5 左 右 左
となり, フラクタルの新興勢力は, 赤か青の新興勢力の方向と合っている. 当然青と赤の新興勢力は, 逆向きだ.
dragon曲線の新興勢力が, どういう向きに出来るかは未検討だが, 「低気圧が来たので天気が崩れる」程度の, 一応の説明にはなったかもしれない.
しかしこれは, 「高気圧は下にあり, 台風は右上に進む」といっているようなもので, もう少し定量的な説明は出来ないかと思った. そして注目したのは, 折り目の点である. dragon曲線は, もともと紙を半分に, 半分に,...と折って作ったことになっているので, その辺に再帰のヒントはないかと考えた.
下の図は64辺からなるdragon曲線で, 端点と曲がり角には0から順に番号を振ってある. 最初の折り目は, 左中央やや下の32番である. その次は16番と48番になる. そこで32番から16番と48番への関係をみると, ちょうど真上と真横にあった(赤線). 次に16番から8番と24番を見ると, ちょうど斜め方向にあった(緑線). 次を見ると再び真下と真横(橙線), さらに斜め線が見えてきた(青色). しかも隣りとの長さは, 順に4, 2√2, 2, √2である. これでもうtwindragonの仲間であることがほとんど判明した.
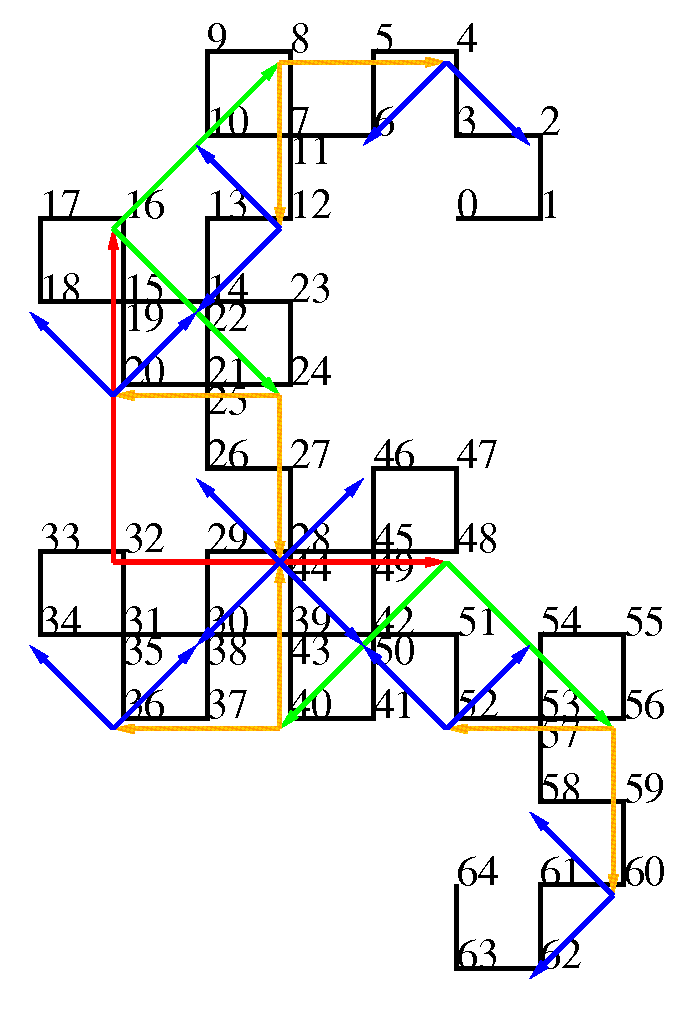
図がごちゃごちゃしないように省いた, 最後の折り目間の関係は, 点4k+2からそのプラスマイナス1へである. つまり2から1へと3へ, 6から5へと7へと,...,62から61へと63へと, である. 描いてはないが想像出来る.
ここまでくると, TAOCP風の筆法に従えば, 後は「演習問題参照」となる.
それにしても, こういう絵がすぐ描けて, テストも出来るし, 説明も出来るし, お絵書きプログラムは, 私にとって神様仏様だ.