単調関数

The Art of Computer Programming の先の方を読んでいたら, monotone-function function というのに出会った. もちろん, monotoneな関数とは, 単調な, 俗語でいえば「右肩上がり」か「右肩下がり」なものである.

しかし単調関数の関数となると, どうもそう簡単なものではないらしい. そこでの説明は以下の通り. 式が多いので, texで書いて張り付けてある.



上のμ_nの式の右辺のbigwedgeの下にある, 0≤i⊆j≤2ⁿは, 「nビットのiの各ビットがjの各ビットより大きくない対について」という意味である.

TAOCP流にいうと, the bit string i=i₀...i_n-1 is regarded as contained in or equal to the bitstring j=j₀...j_n-1 if and only if i_k≤j_kfor all k.


これでやってみるとmonotone functionは
0変数で2種類(0, 1),
1変数で3種類(0, x, 1),
2変数で6種類(0, x∧y, x, y, x&ory, 1)あり,
3変数の20種類は以下のとおりである.
0, (∧ x (∧ y z)), (∧ y z), (∧ z x), (∧ (∨ x y) z), z, (∧ x y), (∧ (∨ z x) y), y, (∧ (∨ y z) x), (∨ (∧ x y) (∨ (∧ y z) (∧ z x))), (∨ (∧ x y) z), (∨ (∧ z x) y), (∨ y z), x, (∨ (∧ y z) x), (∨ z x), (∨ x y), (∨ x (∨ y z)), 1

3変数関数はSchemeでチェックしたので, Cambridge Notationになっている.
monotone functionは否定なしで, ∧, ∨ だけで書けるというのはこれで分かる.



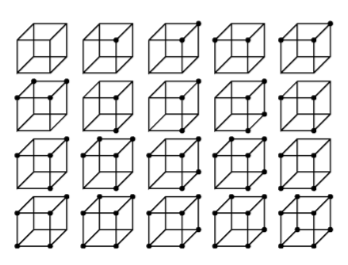
この図では, 各キューブが1つのmonotonic functionを示す. 座標軸はxが手前, yが右, zが上である. 角の黒丸が関数値が1になることを示す. 左上が3変数関数の0に, その右隣りがx∧y∧zに, のように対応している. 右下が最後の1である. 大学にいた頃, monotonic functionは, このキューブを羊羮だと考え, 黒丸のコーナーと黒丸なしのコーナーが包丁で一度に切り分けられるもの, といったことがある.その様子は見て取れよう.

ついでだが, この図で黒丸の数は0から8まである. 0個の関数は1, 8個のは1である.
1個のは x ∧ y ∧ z, 7個のは x ∨ y ∨ zである.
2個のは x ∧ y 型, 6個のは x ∨ y 型だ.
3個のは x ∧ (y ∨ z)型, 5個のは x ∨ (y ∧ z)型.
4個のは x 型か (x ∧ y) ∨ (y ∧ z) ∨ (z ∧ x)=(x ∨ y) ∧ (y ∨ z) ∧ (z ∨ x) これは自己相対で<x, y, z> (多数決)である.

μ_nの真理値表は以下の通り:

μ₀=(1,1)
μ₁=(1,0,1,1)
μ₂=(1,0,0,0,0,0,0,0,1,0,1,0,1,0,1,1)

最後の真理値表から, 2変数関数が単調になる真理値は(一番左を0番として)
0,0,0,0(0番)
1,0,0,0(8番)
1,0,1,0(10番)
1,1,0,0(12番)
1,1,1,0(14番)
1,1,1,1(15番)
だから, 0,0,0,0は0に, 1,0,0,0はx∧yに, 1,0,1,0はyに, 1,1,0,0はxに, 1,1,1,0はx∨yに, 1,1,1,1は1に対応する.

この出てきた文脈は, BDD(binary decision diagram)の合成である. これについてはまたにしよう.