差動歯車は自動車の駆動装置に使われていることでよく知られている. 息子が小学校の上級のころ, プラモデルで無線操縦のレーシングカーを作るのを見ていたら, プラスティック製の差動歯車の部品があり, それで差動歯車を組み立て, 中にグリースを詰めて密封していた. こんなところまでこだわるのかと恐れ入った.
差動歯車の構造を下のようである.
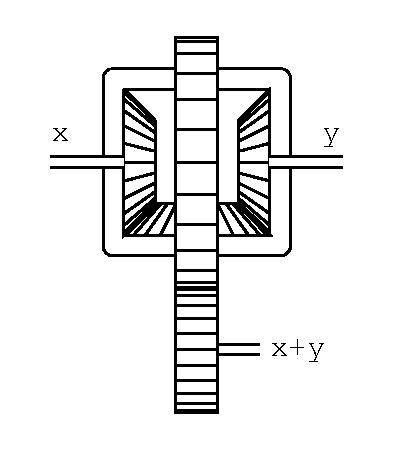
四角で表す箱状のものに, かさ歯車が3つ入っている. 左右のかさ歯車はそれぞれ外部のx軸, y軸に連結している. 図に見るように, x軸とy軸は直接にはつながってはいない. 中央下のかさ歯車は, 左右のかさ歯車に噛み合い, 軸は箱状のものに刺っている. x軸, y軸が同方向に同速度で廻転すると, 中央のかさ歯車は, 自分の軸の周りには廻転せず, 箱状のものをx, y軸の周りに, 同速度で廻転させる. 箱状のものがx, y軸の周りに廻転すると, それと一体の歯車もxやyと同様に廻る.
xの廻転を止め, yだけ廻転させると, 下のかさ歯車が廻転しながら, 箱状のもの(z軸といおう)も廻転する. しかし今度はyの半分である. z=(x+y)/2なのだ.
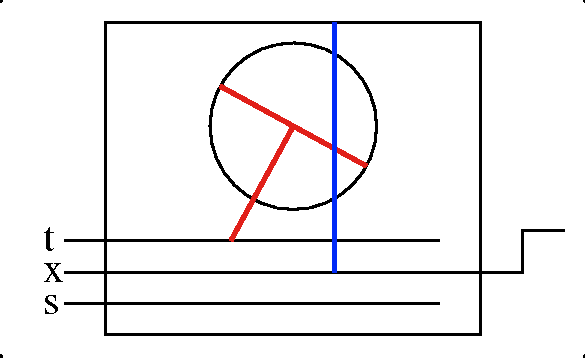
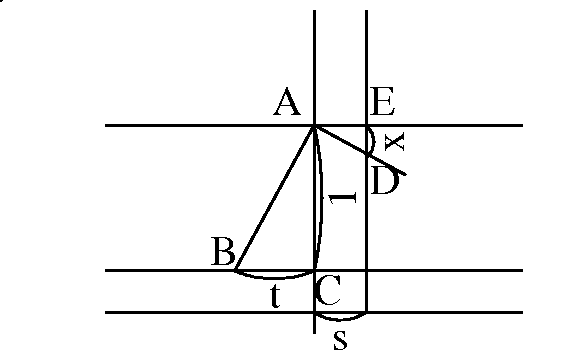
作動歯車の動きを滑車で表すと次の図のaのようになる. 滑車に紐をかけ, 両端をxとyだけ引くと, 滑車(下のかさ歯車に相当)は廻転せずに同じ長さだけ下がる. bはxを引かない時で, 滑車は廻転し, yの半分だけ下がる.
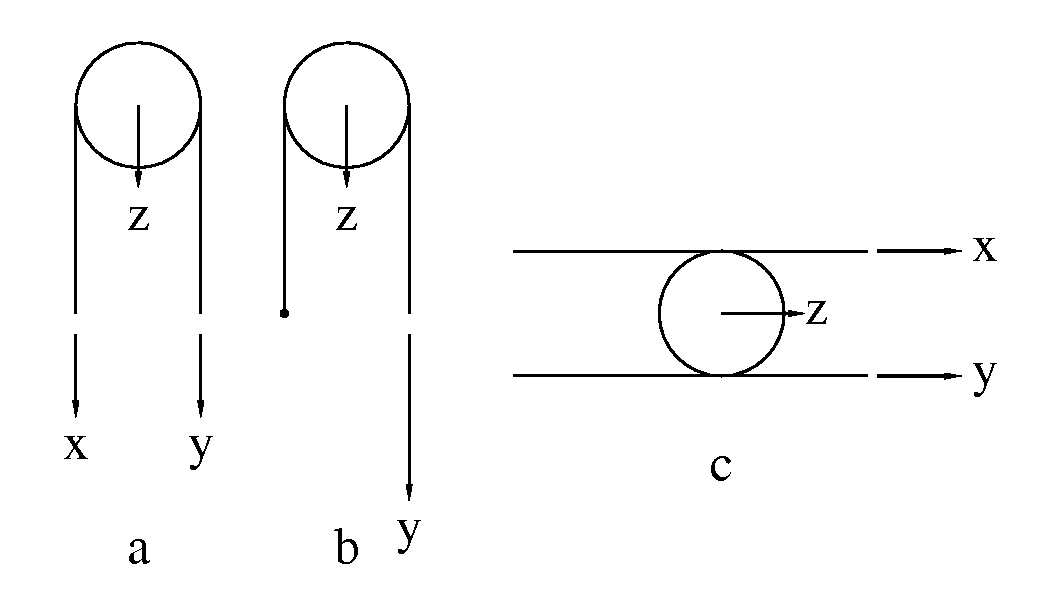
滑車が廻転するのは, 紐が滑らないことなので, 紐の代りに滑らない棒を使っても同じなことをcは示す. これはxとyのかさ歯車を展開したものである.
図では箱状の歯車を半分の歯の歯車に噛ませて(2倍して), x+yが出来ることを示す.
自動車のいわゆるデフは, このx+yの軸が駆動軸で, 両車輪xとyを駆動する. エンジン(ミッション)からの駆動軸は車軸と直交するので, この歯車はかさ歯車である.
ところで通常デフといわれる装置は, 最初に書いたように, ディファレンシャルである. ディジタルをデジタルというのに似た変形である.
佐々木達治郎先生の「計算機械」(1947年刊)に東大航空研で試作した微分解析機の構造が説明してあり, その中に機素の加算に遊星歯車(planetary gear)を使うと書いてあった.
遊星歯車といえば, 内装式の自転車の変速機が有名である. 昔の通信機器は, 同調ダイアルにやはり遊星歯車を使っていた. つまり背後に丸い文字版があり, 手前に黒いつまみがある. つまみを廻しても, 文字版ははるかに遅く廻り, 微妙な同調が出来るようになっていた. 文字版には副尺もついていて, 高級感を出していた.
下が遊星歯車の図解である.
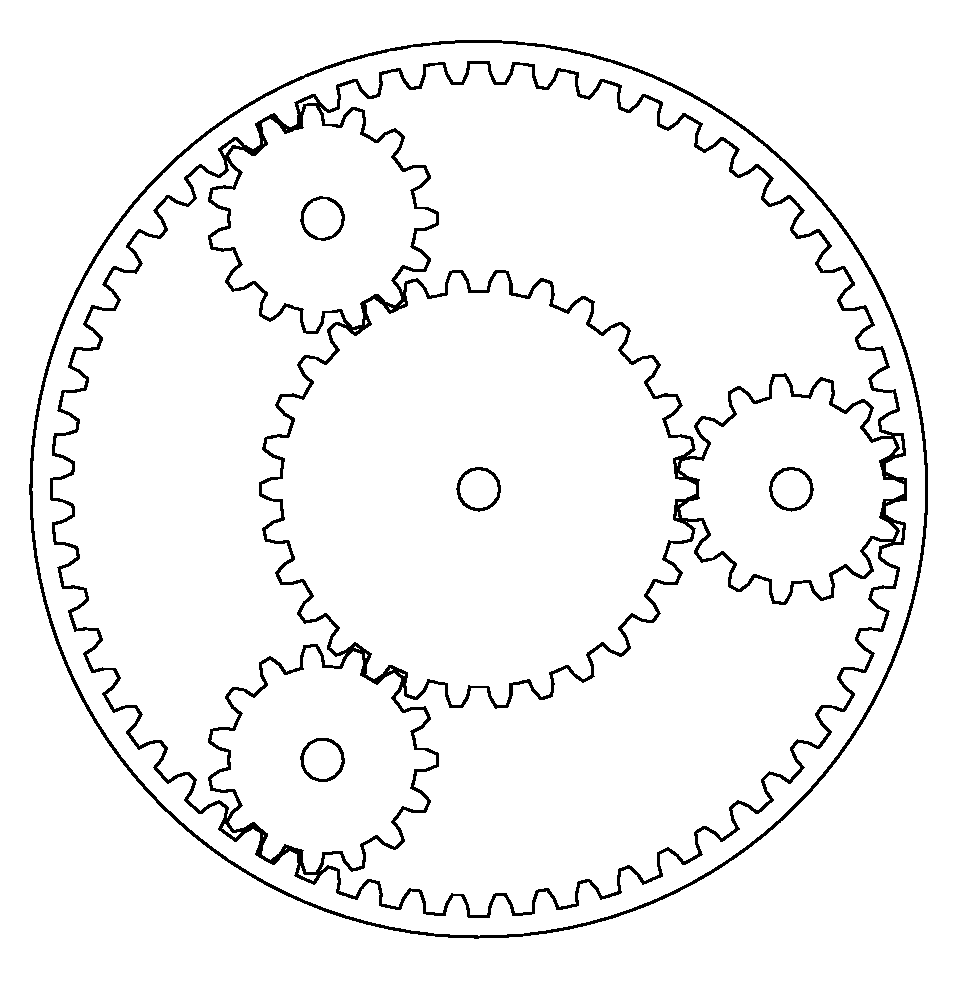
中央の太陽歯車の廻りに同じ大きさの遊星歯車があり, 遊星歯車は太陽と外側の(内向きに歯を持つ)歯車に噛み合う. また遊星歯車の軸は遊星キャリヤに乗っていて, 歯車の位置が変るとキャリヤの軸も廻転する. (こういう絵を描くのは楽しい.)
これでどうして差動歯車になるか, 即座には分からないが, もう1つの絵を描いてみると納得出来る.
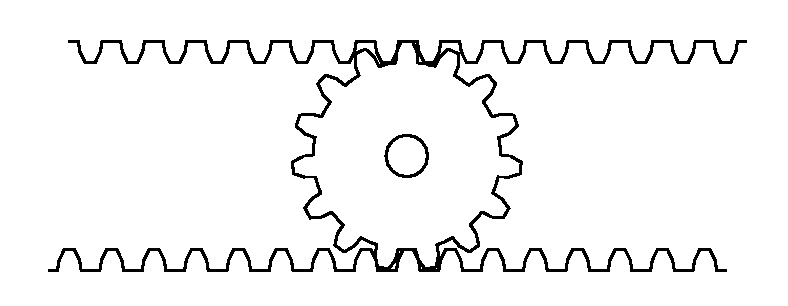
これは太陽歯車と, 外側の歯車を1列に延したもので, 一応遊星歯車と等価を考えられる. 太陽歯車の廻転は下の棒状の歯車(ラック)の移動, 外側のは上の歯車の移動であり, キャリヤの軸の廻転は中央の歯車の軸の左右の移動と思えばよい.
歯車の場合は, 廻転角度が重要な情報だが, ラックでは移動の歯数で考えることになる.
こういう絵をみると, 上の差動歯車と同じになり, なるほど加算機構に使えるを分かる.
差動歯車の解説を読むと, かさ歯車のものより, 遊星歯車型の方が基本のように書いてあった. われわれは車の知識があるので, かさ歯車が一般的を思い込んでいたようである.