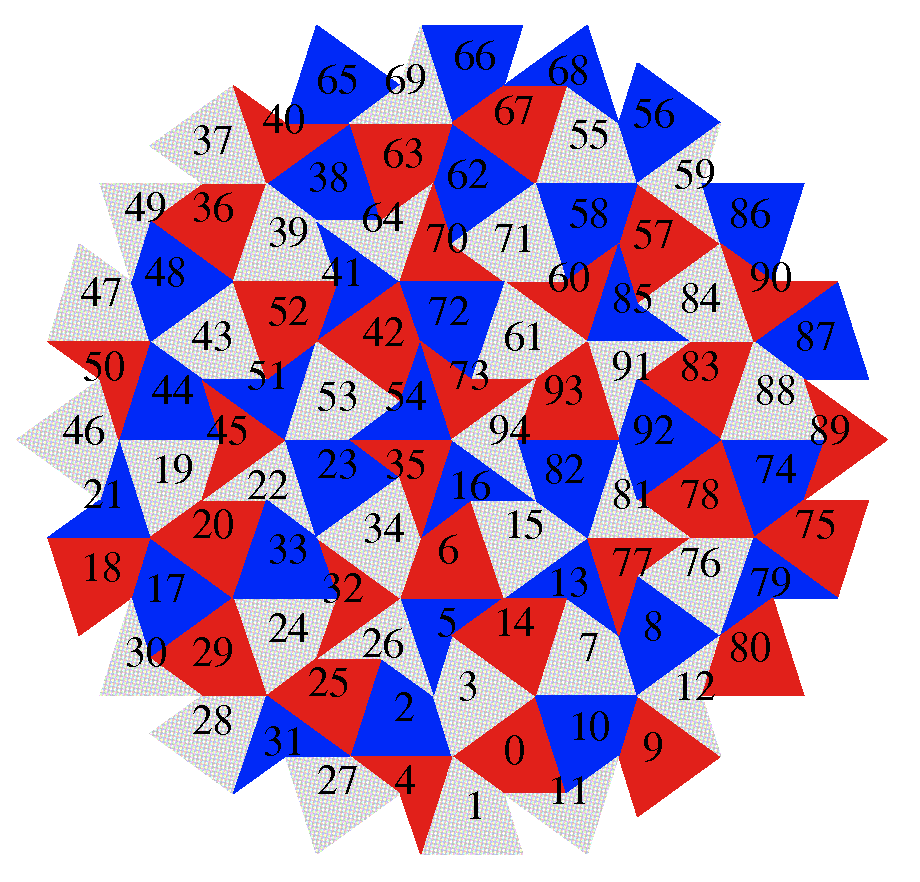
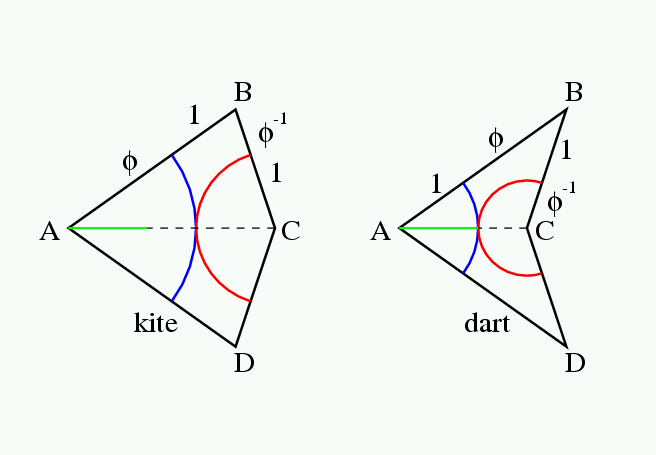
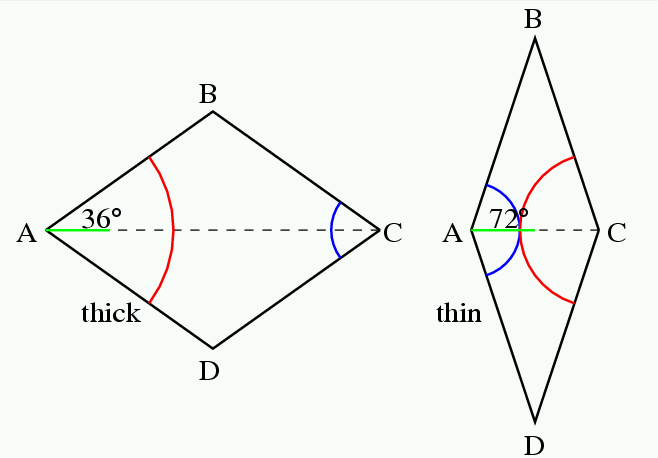
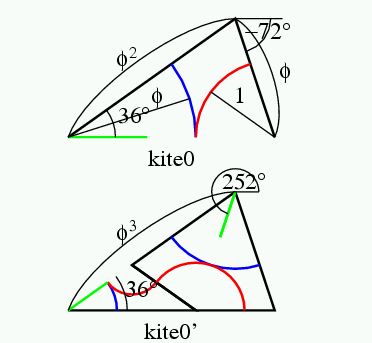
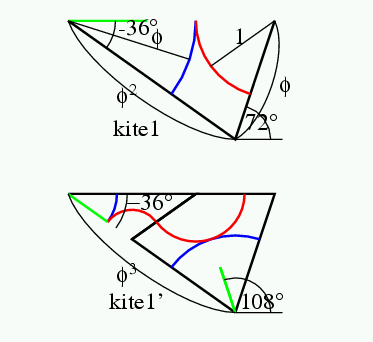
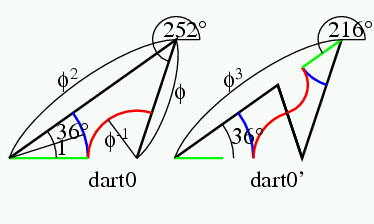
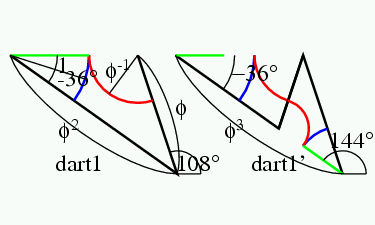
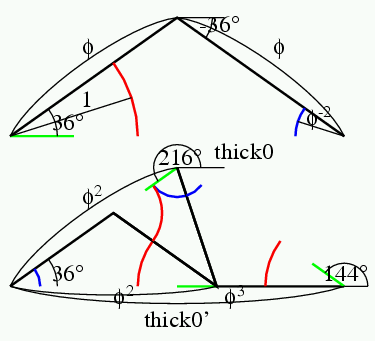
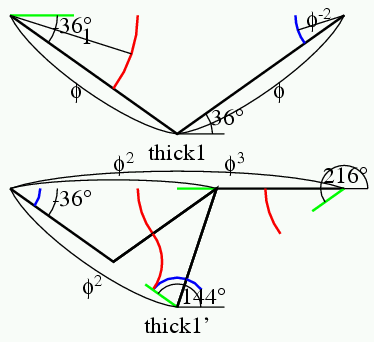
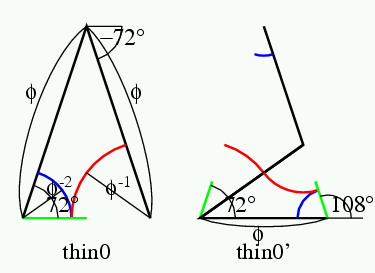
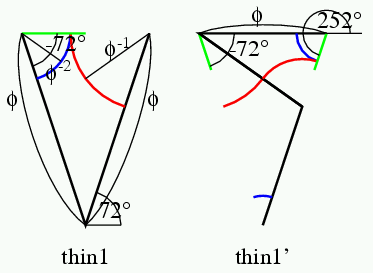
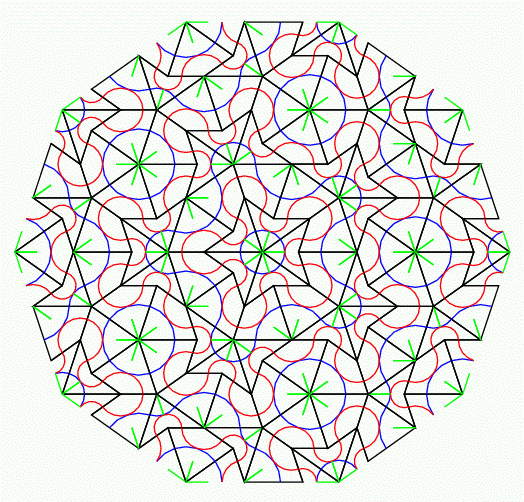
余談だが, 慶應の皆さんは, 慶應の校旗はblue red and blueの3色といい, 私の2010年5月13日のブログのように, オランダ国旗も3色だ. ジャジャーン.言語学者の用語では, 「サイタ サイタ サクラ ガ サイタ」は, 延べ語数5,異なり語数3という. その伝では, 慶應の校旗は述べ3色旗. オランダ国旗は異なり3色旗である. Penrose tileは異なり3色で塗り分け可能である.
数学者なら, 3色塗り分け可能を証明するわけだが, 私の場合はプログラムで,3色塗り分けしたい. さっそくトライ.
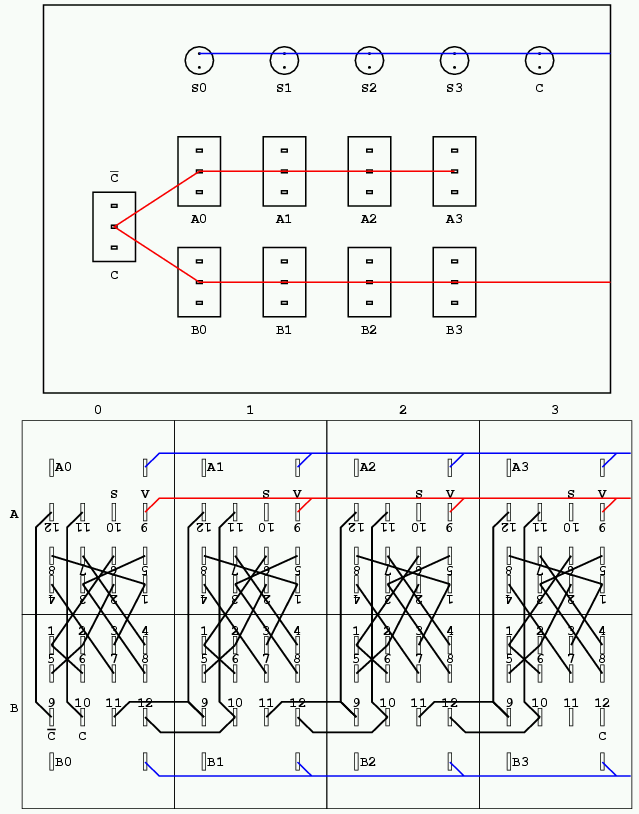
前回のブログの最後にプログラムがあるが, そこで分かるように, それぞれの線分はtranslateで原点を移動し, rotateで向きを変えたユーザ座標て描いている. これでは誰が隣りかは判明しない. どうすれば絶対座標(装置座標)で描けるか, PostScriptのマニュアルをみると, transformという関数がある. PostScriptでは,装置座標とユーザ座標の関係は, current matrixが記憶していて, transformはユーザ座標を装置座標にしてくれるらしい.
ところが,例えば kite0のn=0の部分を0 0 transform == phi2 36 xy transform == phi -72 xy transform ==のようにし,
[1 0 0 1 0 0] setmatrix
300 400 translate
/n 0 def init
0 0 0 kite0
で起動すると, kite0の3点は,
A 300.0 400.0
B 469.442719 523.107361
C 340.0 276.892639
と出力された.
今, 単位長さが80なので, すこし計算してみる.
(* 80 phi phi (cos (d2r 36))) => 169.4427190999916
(* 80 phi phi (sin (d2r 36))) => 123.10734148701015
(* 80 phi (cos (d2r -72)) => 40.00000000000001
(* 80 phi (sin (d2r -72))) => -123.10734148701013
理由は分からないが, AとBは正しい; CはAから-72度の方向に移動した距離になっている. それが分かればあとはプログラムでCの位置は計算出来る.
こうしてkite0, kite1, dart0, dart1の3点の座標が得られた. 次はkite0とkite1, dart0とdart1を組合わせる. 始点と終点は合っているから, それらを対にする. 相棒のないのは外す. こうして95の四辺形が揃った. 各四辺形には0から94まで番号をつける.
次は隣りどうしを探す作業で, alistを作り, 辺を登録したり探索したりして,隣組のリストが出来た. 両方から指すこともないので, 自分より番号の少ない隣りの四辺形のリストになっている.
次にそれぞれに色0,1,2を対応させる. 目で見てやるのと違うから,バックトラックすることになる. SICPの8クィーン(ex2.42)のプログラムをちょっと改造して書いてみたが, これは全解探索だし, 深さも8段から95段になるので,たちまち再帰のオーバーフローを起した. うーん. 駄目か.
仕方ないので, 通常のバックトラックのプログラムを書く.解が1つ見つかったところで, call-ccを使って脱出する.
(define next' (() (0) () (0 2) (2 1) (3) (5) () (7) ()
(7 9 0) (10 0) (9 8) (7) (7 13 5 3) (6 13) (15 6) () (17) ()
(17 19) (19 18) (20) (22) () (24 2) (25 2 5) (4) ()
(24 28 17) (29 17) (28 27 25) (24 26) (24 32 22 20)
(23 6 32) (16 34 23) () (36) () (36 38) (38 37) (39) (41) ()
(43 19) (44 19 22) (21) () (43 47 36) (48 36) (47 46 44)
(43 45) (43 51 41 39) (42 23 51) (35 53 42) () (55) ()
(55 57) (57 56) (58) (60) () (62 38) (63 38 41) (40) ()
(62 66 55) (67 55) (66 65 63) (62 64) (62 70 60 58)
(61 42 70) (54 72 61) () (74) (8) (76 8 13) (74 76) (76 75)
(79 12) (78 77) (81 15) () (83 57) (84 57 60) (59) ()
(83 87 74) (88 74) (87 86 84) (83 85) (83 91 81 78)
(82 61 91) (73 93 82 16)))
(define colorlist '())
(define (search)
(call-with-current-continuation
(lambda (throw)
(define (safe? n c)
(let ((es (list-ref next n)) (revc (reverse colorlist)))
(not (member c (map (lambda (x) (list-ref revc x)) es)))))
(define (test n)
(if (= n 95) (throw (reverse colorlist))
(do ((m 0 (+ m 1))) ((= m 3))
(let ((c (modulo (+ m n) 3)))
(if (safe? n c)
(begin (set! colorlist (cons c colorlist))
(test (+ n 1))
(set! colorlist (cdr colorlist))))))))
(test 0))))
(search)
ジャジャーン. これでやっと色のリストが得られた.
(0 1 2 1 0 2 0 1 2 0 2 1 1 2 0 1 2 2 0 1 0 2 1 2 1 0 1 1 1 0
1 2 0 2 1 0 0 1 2 1 0 2 0 1 2 0 1 1 2 1 0 2 0 1 2 1 2 0 2 1
0 1 2 0 1 2 2 0 2 1 0 1 2 0 2 0 1 0 0 2 0 1 2 0 1 2 2 2 1 0
0 1 2 0 1)
結果はご覧の通り.