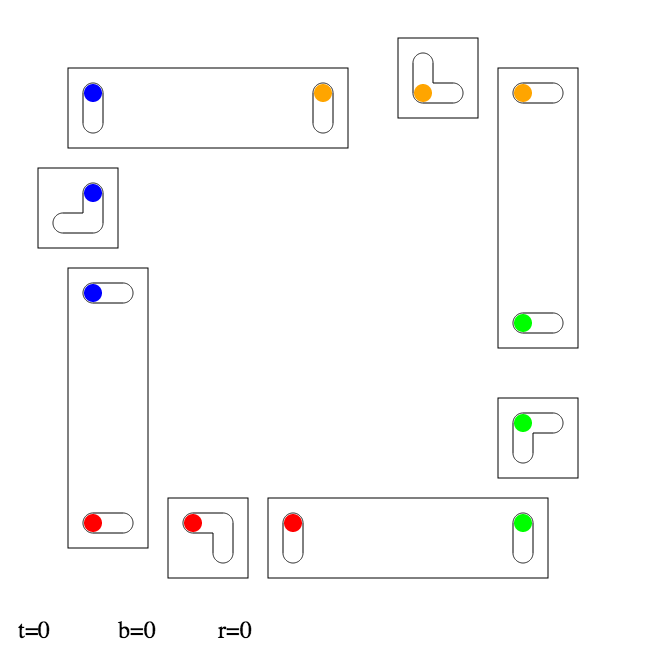
EDSACのプログラムを集積した
ウェブページがある. (詳しくはそこの
"To browse the collection of software, click this link."をクリックする.)
ここには私の書いたエラトステネスの篩も置いてあって嬉しい(21行目). そこにDavid J. Wheelerの素数のプログラムがあった(15行目). Martin Campbell-Kellyの書いたEDSACの文献(Programming the EDSAC: Early Programming Activity at the University of Cambridge, IEEE Annals of the History of Computing, Vol 1, No. 2.)によると, EDSACには「EDSACの本」で有名なイニシアルオーダーの前にもう一つのイニシアルオーダーがあって, 1949年5月6日の運転開始の日にはその方が使われていた. 同年6月22日にケンブリッジで開催された計算機会議でEDSACが公開され, その時, Wilkesの書いた平方の表とWheelerの書いた素数のプログラムのデモが行われた.
Wheelerは1927年生まれだから, 22歳のWheelerが当時どういうプログラムを書いていたかには非常に興味がある. これはもう読むしかない.
ところがその内容たるや
[Primes]
T107SO92SO93SO94SS5ST6SO95SO95ST7S
A96SR4SS97SE42SL4SA97SG45SS98SG100ST7S
A97SA4ST97SH97SN97SL64SL64SA96SE39ST7S
A96SU1SA4ST96SA99ST97SS88ST7SH91SA1S
E72SV91SS89SE71SA89STLOSH90SV1SL4S
TLA7SA98SG67SA6SA4SG36SE33SP2SP500S
JSP16S#S@S&S!SP2LP1LPLP1L
T7SA99ST97SA4SA96ST96SE39S
だけなのだ. これを読む手がかりは
ここにある.
読んでみると, やはり面白いプログラムであった. 特にそのプリントルーチンには感心した. 以下にその解説をしたい.
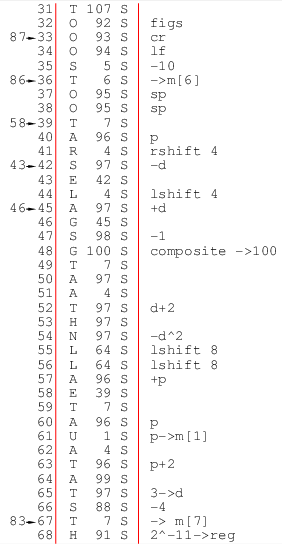

31番地 T107S. このプログラムは最初のイニシアルオーダーInitial Order1で読み込むが, 読み込まれるプログラムが106番地まであるなら, 最初をT107Sとするのであった. つまりイニシアルオーダーには格納命令があり, 最初はT31Sになっていて, 31番地から命令を格納する. つまり, T31S, T32S, ..と変わっていく. そして格納作業の終りは, 格納命令から31番地にある命令を引き, それが正であるかを見る. T107Sを引くと0(正)になるので31番地へ進んでくる. このT命令はアキュムレータのクリア用にも見えるが, すでに0になっている.
32番地は92番地にある#S(figure shift)を出力する. 以下のプログラムが数字を出力するので, その準備.
33,34番地では93, 94番地にある@S(cr), $S(lf)を出力. 次のS5Sはイニシアルオーダーの5番地にあるP5S(10*2^-16)を引き, -10を作り, 6番地(m[6])に入れる. 6番地は
-10,-8,-6,..と変わり, 1行に5個の素数を印刷する.
37, 38番地. !S(space)を2個出力. (このプログラムのあちこちにある)T7Sは(67番地のものを除いて)アキュムレータをクリアする.
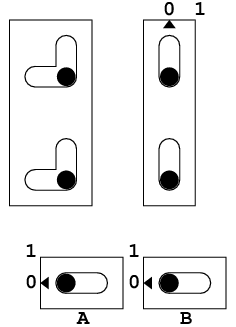
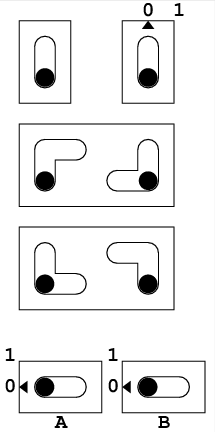
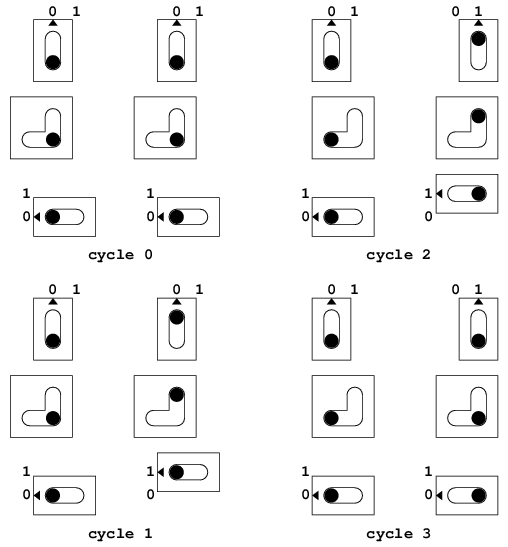
このプログラムでは素数の候補pから3,5,...と奇数(d)を引き(以後 dを減数という), 0になるかどうかを見ている. (前にも書いたようにEDSACには除算命令はない.) pは96番地, dは97番地にあって, それぞれ5と3に初期化されている.
40から46番地はそのpからdを引く. ただ初めは16*dを負になるまで引き, 次にdを正になるまで足す. これでpをdで割った剰余が得られる. 実際には16*dを引くのではなく, pを4ビット右シフトして引き, 4ビット左シフトして足す. (おおざっぱにいうと単にdを引くより, 16倍加速されている. こういう剰余の取り方はEratosthenesの篩でも使える.)
47番地. EDSACには零ジャンプがないので, 正になったところで1を引き, 負なら零であったということで, 合成数の判定をして100番地へ進む.
剰余が0でなければ, 50,51,52番地でdを2増やし, 53番地からH97Sで乗算レジスタにdを置き, N97S, L64S, L64Sで-d^2を作る. それにpを足し, 減数の二乗が素数候補より小さければ39番地へ戻り, 次のテストに掛かる.
減数が大きくなって素数と判定出来ると, 60番地から先で素数の出力にとり掛かる.
U1Sで素数を1番地に入れ, A4Sでpを2増やして63番地で96番地に入れておく.
素数は4桁で出力するつもりで, 66番地で-4を7番地のカウンタへ入れる.
68番地から76番地は1桁の出力で, 1番地に1234があるとして説明すると, 68番地H91Sで乗算レジスタに2^-11を入れる(32*2^-16=2^-11).
アキュムレータに1234を足す. 72番地へ飛んで89番地にある1000を引く. アキュムレータは234(*2^-16)になり, 正なので71番地へ行く. V91Sだからアキュムレータは234*2^-16+2^-22になる.
再び1000を引くと今度は負になり, 74番地で1000を足し, アキュムレータは234*2^-16+2^-22に戻る.
これを0番地の長語に入れる. つまり左半分の1番地は234, 右半分の0番地はファンクション部に1となる. そこでo命令は0番地を出力するから1が印字される(EDSACの文字コードは2012年9月28日のこのブログ参照).
77番地から80番地は234を10倍する. H90Sで乗算レジスタに10*2^-4を置き, V1Sでアキュムレータは234*10*2^-4になり, 次の左シフトで2340になり, 1番地に戻される.
81番地からは7番地のカウンタを1足し, まだ4桁出力していなければ, 67番地へ戻る.
次は2340だから, 71番地のループは2回実行され, 右半分の方は2*2^-11になって2が印字され, 1番地は3400になる.
4桁出力すると84番地へ来て, 6番地のカウンタにA4Sで2を足し, 5個未満なら36番地, 5個終わっていたら33番地へ戻る.
一方合成数の時は100番地へ進み, 101, 102番地でdを3に戻し, 103,104,105番地でpを2増やして39へ戻る.
この解釈が正しければ, 期待される出力は
0005 0007 0011 0013 0019
0019 0023 0029 0031 0037
...
なる筈であった. サイボウズ・ラボの西尾君がEDSACのシミュレータを持っているというので, 試してもらったらその通りであったとメイルが来た.
このプログラムの疑問は素数候補が5から始まることである.
減数を3から始めると素数候補の3は割り切れるから, 3は素数にならない. 3を素数にするには2から割り始めなければならないからなのだ.