Martin Gardnerの本に30 color cubesという話題があった.
立方体には面が6つある. それに相異なる6色を塗る. 廻転して同じになるようなものは作らないとすると, 30通りの塗り方がある.
6色を0,1,2,...,5とする. 立方体の面にも名前をつける. 島内剛一先生の「ルービック・キューブと数学パズル」にあったように, 上をtopのt, 下をbottomのb, 北をn, 東をe, 南をs, 西をwとするのは, 常識だろう. これを(t n e s w b)の順に並べることにする.
まずtを基準として色0を割当てる. するとbには, 他の5色のいずれかが来る. そして残りの4色で側面を塗るが, 4色の最小の色をnに割当てると, 後は3色の置換の6通りになり, 都合30通りというわけだ.
こんなプログラムを書いた.
(define (gencubes)
(let ((t 0) (neswb '(1 2 3 4 5)))
(apply append (map (lambda (b)
(let* ((nesw (delete b neswb)) (n (apply min nesw))
(esw (delete n nesw)))
(map (lambda (esw) (append (list t n) esw (list b)))
(permutation esw)))) neswb))))
2行目でtを0, neswbを(1 2 3 4 5)とし, 3行目のmapのlambda変数でそのいずれかをbとする. neswbからbを除いたものがneswで, その最小をn, 残りをeswとした. それの辞書式順の置換を作り, 前に(t n), 後に(b)をappendして30通りを作っている.
((0 2 3 4 5 1) (0 2 3 5 4 1) (0 2 4 3 5 1) (0 2 4 5 3 1)
(0 2 5 3 4 1) (0 2 5 4 3 1) (0 1 3 4 5 2) (0 1 3 5 4 2)
(0 1 4 3 5 2) (0 1 4 5 3 2) (0 1 5 3 4 2) (0 1 5 4 3 2)
(0 1 2 4 5 3) (0 1 2 5 4 3) (0 1 4 2 5 3) (0 1 4 5 2 3)
(0 1 5 2 4 3) (0 1 5 4 2 3) (0 1 2 3 5 4) (0 1 2 5 3 4)
(0 1 3 2 5 4) (0 1 3 5 2 4) (0 1 5 2 3 4) (0 1 5 3 2 4)
(0 1 2 3 4 5) (0 1 2 4 3 5) (0 1 3 2 4 5) (0 1 3 4 2 5)
(0 1 4 2 3 5) (0 1 4 3 2 5))
これを辞書式順にソートしたものを, 0は白, 1は赤, 2は緑, 3は青, 4は橙, 5は黒として表示したのが, 以下の図である.

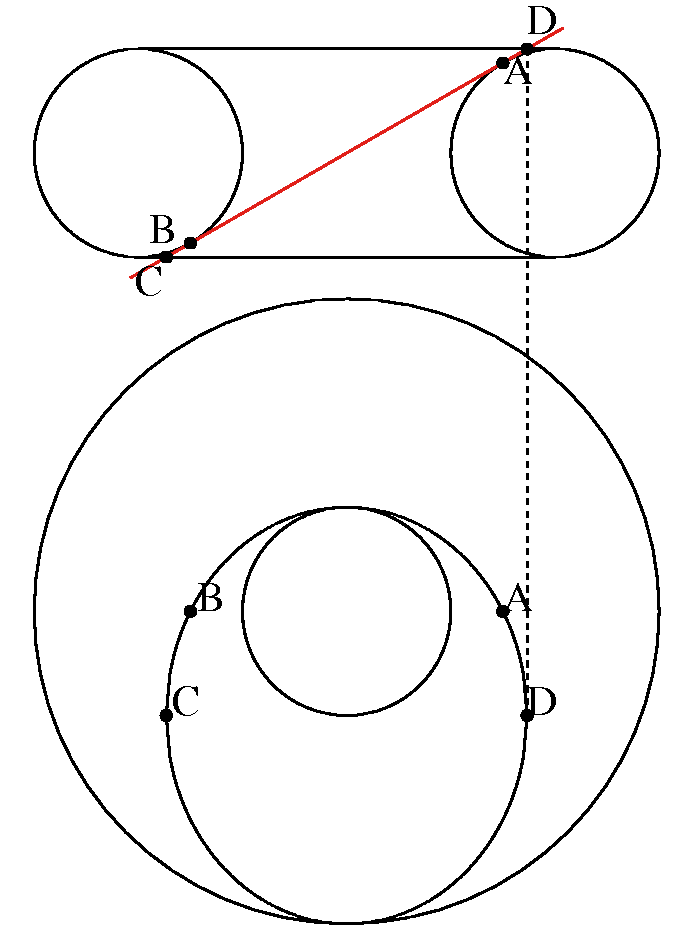
左上の0番で説明すると, それぞれは2つの6角形が連接した形になっていて, 左の6角形は立方体を北東の上方から眺めたもので, t,n,eの3つの面がそれぞれ菱形で表示してある. 上にt=0, 右下にn=1, 左下にe=2の面が見える. 一方, 右の6角形は,南西の下方から眺めたもので, 右上にs=3, 左上にw=4, 下にb=5の面がある. wの4とnの1は, 図でつながっているだけでなく, 実物でもつながっている. 立方体の側面は, 1,2,3,4と北から右まわりにつながっている様子が描いてある.
そこでクイズなのだが, 仮にいま話題にした0番を見本とすると, 他の立方体から8個を選び, 2x2x2のちょうど2倍の立方体を作り, その立方体の外方の面を見本と同じ色にし, 立方体の内側で相接している面同士は, 同じ色にするというのである.
通常なら, 積み木を用意し, とっかえひっかえやってみることになるわけだが, そこはやはりプログラムで全解探索せざるべからずである.
そしてやってみた結果が下の図で, 解は2通りあった.

この図の見方は, それぞれの解で, 大型の菱形に配置した4個の立方体が上下2段に描いてある. 上の4個がそのまま上段に, 下の4個が下段になる. それぞれの菱形の下(0と4)が北東, 左(1と5)が南東, 上(2と6)が南西, 右(3と7)が北西を占める. それぞれの解で, 上段の4個(0,1,2,3)のtは0, 下段の4個(4,5,6,7)のbは5, 北の4個(0,3,7,4)のnは1,...のように, 外の6面は4個ずつ見本と同じである. また相接する面も, 例えば上の解の1のb=4は5のt=4で一致しているし, 1のn=5は0のs=5で一致している.
プログラムは通常の深さ優先の探索木を辿るものである. 解の図のように, 8個の立方体を0,1,2,...の順で候補を探す. そのため, ある立方体をあらゆる方向から見た24個を作るプログラムと, (0 1 2 () () ())のようなパターンと, ある立方体の色の順が, 合っているかを見るプログラムを用意した.
探し方は以下の通り.
探すパターン 決った色
c0 (t n e - - -) s0 w0 b0
c1 (t s0 e s - -) w1 b1
c2 (t - w1 s w -) n2 b2
c3 (t n w0 n2 w -) b3
c4 (b0 n e - - b) s4 w4
c5 (b1 s4 e s - b) w5
c6 (b2 - w5 s w b) n6
c7 (b3 n w4 n6 w b)
30通りの立体の組を全候補とする. その中から見本を選ぶ. 上の例では0番. 見本からt, n, e, s, w, bを設定する. 全候補から見本を除いたものをc0用候補とし, そこからc0のパターンに合ったものをc0とする. c0が決るとs0, w0, b0も決る. c0用候補からからc0を除いたものをc1用候補とし, そこからc1のパターンに合ったものをc1とする. c1が決るとw1, b1も決る. 以下同様にしてc7まで決ればc0,c1,...c7を出力する.
プログラムはこれだけである.
30種の立方体は, 全て対称的に出来ているから, 0番を見本とする解が得られれば, 1番,...,29番を見本とする解もまったく同様に作れる. 実際プログラムがあるのだから, 全部やってみた. 全く同じような解が2つずつ得られた.
追記 上と下の解で使われている立方体の番号(上の図参照)は, それぞれ
6 4
22 7 1 16
19 12
12 19
16 1 7 22
4 6
であり, 2つの解で同じ組み合せであった.