復活祭(Easter)の日取りは, 春分かその後の最初の満月の後の日曜で決るから, このアルゴリズムに関心を持つ人は少なくない.
Knuth先生のThe Art of Computer Programming(TAOCP)にも演習問題として使われている. (TAOCP Vol.1,3rd Ed.,ex1.3.2-14, Fasc1.1,ex1.3.2'-32). 私も興味を持っていて, 数セミの1982年9月号に書いたりしたので, それを知った杉本敏夫さんや新井正夫さんが資料を送ってくださったことがある.
春分とか満月とか天体の運行に関連して日が決るように思えるが, 実は春分は3月21日に固定するとか, 年初の月齢を使うとか, アルゴリズムで決っているのである. とはいえ, TAOCPの演習問題でも分かるように, 結構面倒である.
先日, 以前頂いた資料をのんびりと見ていたら, Gaussの公式というのがあった. これは意外と簡単であった.
(define (easter20 y)
(let* ((m 24) (n 5) (a (modulo y 19)) (b (modulo y 4))
(c (modulo y 7)) (d (modulo (+ (* 19 a) m) 30))
(e (modulo (+ (* 2 b) (* 4 c) (* 6 d) n) 7)))
(if (> (+ d e) 9) (list 'april (+ d e -9))
(list 'march (+ 22 d e)))))
という具合いに剰余しかとらない. let*の始めの方のmとnは世紀に依存する定数で, 2000年から2099年までは24と5である. そのため関数名に20をつけた. 杉本さんの資料に詳しい説明があるが, その話はまたいつかにして, 今回はReingoldとDershowitzのCalendrical Calculationsにある復活祭公式の話だ.
簡単にいえば, 計算法はKnuthのアルゴリズムと同様である. ただ計算の記述が本書では一風変っているので, その辺の話をしたい.
この本では, 日の計算に, fixed day number (fixed dateとかR.D.ともいう) の通日を使う. ユリウス日のようなものだが, Gregorian暦が過去まで使われたとして, その1年1月1日を第1日とするのである. その日は月曜なので, fixed dateを7で除した剰余が日曜を0とする曜日と重なって都合が良い,
Gregorian暦は400年毎に繰り返すから, 2001年1月のカレンダーをcal 1 2001で出力してみると
January 2001
S M Tu W Th F S
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
でGregorianの1年1月1日が月曜であることが確認出来る.
Calendrical Calculationのeasterのアルゴリズムはこうだ. Schemeに書き直してある.
(define (easter g-year)
(let* ((century (+ (quotient g-year 100) 1))
(shifted-epact (modulo (+ 14 (* 11 (modulo g-year 19))
(- (quotient (* 3 century) 4))
(quotient (+ 5 (* 8 century)) 25)) 30))
(adjusted-epact
(if
(or (= shifted-epact 0)
(and (= shifted-epact 1) (< 10 (modulo g-year 19))))
(+ shifted-epact 1) shifted-epact))
(paschal-moon (- (fixed-from-gregorian g-year april 19)
adjusted-epact)))
(kday-after paschal-moon sunday)))
最後の行から見ると, easterはpaschal-moon(春分満月)の後の日曜を探すようになっている. kdayというのは, kがsunやmonや...やsaturで, それらをまとめてkdayという. (k曜日ということだ.) つまり春分満月の後の日曜を求めるのだ.
その前のlet*の中は, century(世紀), epact(歳首月齢), paschal-moonなどを計算する. paschal-moonは(fixed-from-gregorian year month day)で, 引数の(Gregorian暦の)年月日のR.D.を計算し, adjusted-epactを引いたものが春分満月であり, その直後の日曜(のfixed date)を計算する.
2012年の復活祭を計算すると, 734601と得られる.
Gregorian暦からR.D.への変換は以下の通り. まず定数を定義する. (ここには今必要なものしか書かない.) 次にその年が閏年であるかみる関数gregorian-leap-year?. そして本体だ.
(define sunday 0) (define april 4)
(define january 1) (define march 3)
(define gregorian-epoch 1)
(define (gregorian-leap-year? g-year)
(and (= (modulo g-year 4) 0)
(not (member (modulo g-year 400) '(100 200 300)))))
(define (fixed-from-gregorian year month day)
(+ gregorian-epoch -1 (* 365 (- year 1))
(quotient (- year 1) 4)
(- (quotient (- year 1) 100)) (quotient (- year 1) 400)
(quotient (- (* 367 month) 362) 12)
(cond ((<= month 2) 0)
((and (> month 2) (gregorian-leap-year? year)) -1)
(else -2))
day))
結構オーソドックスに書いてある. ここで面白いのは, 前月末日までの年内の総日数の計算である. 一応2月が30日あるとして計算する式を用意し, 3月以降を平年か閏年かで補正する.
(map (lambda (m) (quotient (- (* 367 m) 362) 12)) (a2b 1 13))
をやってみると次の上の段が得られる. 次の段は平年の正しい値で, 1,2月はよいが, 3月以降は平年は2, 閏年は1多いので, 補正項を計算する. この結構きわどい係数をどのように見つけたのか.
(0 31 61 92 122 153 183 214 245 275 306 336)
(0 31 59 90 120 151 181 212 243 373 304 334)
月1 2 3 4 5 6 7 8 9 10 11 12
Calendrical Calculationsにはごたごた書いてあるが, 要するにこう導出したらしい.
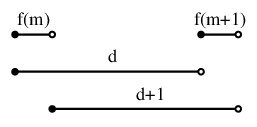
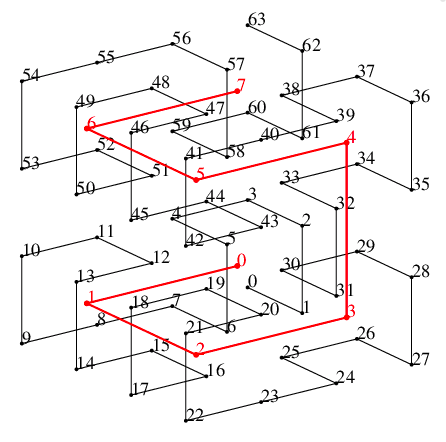
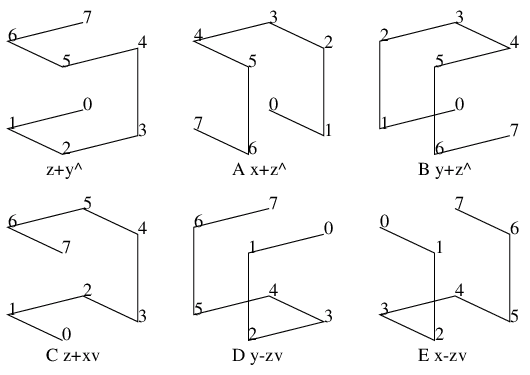
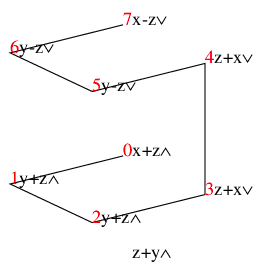
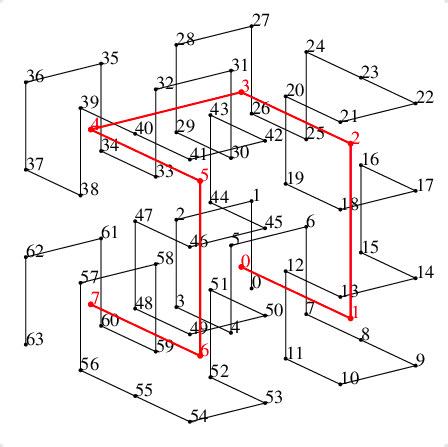
前述のように2月が30日あるとすると, 1年は367日. 12ヶ月に31日の閏月(大の月)を7回平均的に置くとすると, 次のような図が描ける.
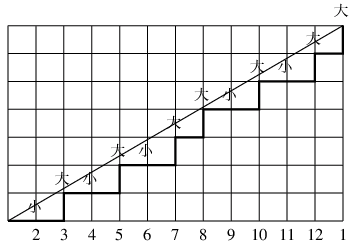
これは勾配7/12の線のfloorをとったもので, 1段上がるときを閏月だと思って1年の月を当てはめると, 図のように大の月と小の月が対応する. すこし位相をずらして見ると
(map (lambda (m) (floor (- (* (/ 7. 12) (+ m 11)) 6))) (a2b 0 12))
=> (0. 1. 1. 2. 2. 3. 3. 4. 5. 5. 6. 6.)
が得られ, 上のリストの1桁目と一致する. これに毎月30日ずつ足せば, 前月までの日数dになるわけだ.
従って上の式のm=0のところを1月に対応させると,
d=floor((7*(m+10))/12-6)+30*(m-1)
=floor((7m+70-72)/12)+(360m-360)/12
=floor((367m-362)/12)
大の月が7, 8月, 12, 1月と並んでいるのも, 結構平均的であったと改めて気づく.
dateの後のk曜の計算は, kday-on-or-beforeを使う.
(define (kday-after date k)
(kday-on-or-before (+ date 7) k))
(define (kday-on-or-before date k)
(- date (day-of-week-from-fixed (- date k))))
(define (day-of-week-from-fixed date) (modulo date 7))
たとえば3月20日の前の水曜(=3)は20日から3を引いた日(17日)の曜日(木=4)を知り, 20日からその4を引いた16日が水曜という計算をする.
さて, 復活祭の日がR.D.で教えられても有難くないから, Gregorian暦に変換する. まずR.D.のある年を計算する.
(define (gregorian-year-from-fixed date)
(let* ((d0 (- date gregorian-epoch))
(n400 (quotient d0 146097)) (d1 (modulo d0 146097))
(n100 (quotient d1 36524)) (d2 (modulo d1 36524))
(n4 (quotient d2 1461)) (d3 (modulo d2 1461))
(n1 (quotient d3 365))
(year (+ (* 400 n400) (* 100 n100) (* 4 n4) n1)))
(if (or (= n100 4) (= n1 4)) year (+ year 1))))
n400は400年のあった回数. d1は400年内の日数. n100は100年のあった回数. d2は100年内の日数. n4は4年の回数. d3は4年内での日数. n1は年の回数. するとdateの年は, yearのようになるが, 閏の調整を最後に行う.
年が判明すると, R.D.の年月日が計算できる.
(define (gregorian-from-fixed date)
(let* ((year (gregorian-year-from-fixed date))
(prior-days
(- date (fixed-from-gregorian year january 1)))
(correction
(cond ((< date (fixed-from-gregorian year march 1)) 0)
((and (>= date (fixed-from-gregorian year march 1))
(gregorian-leap-year? year)) 1)
(else 2)))
(month (quotient
(+ (* 12 (+ prior-days correction)) 373) 367))
(day (- date (fixed-from-gregorian year month 1) -1)))
(list year month day)))
fixed-from-gregorianを何回も使うが, なんとかしたい.
ここでも年内の日数から月を見つける方法がこの本の独特な点である. correctionを別として, 年内日数dからmonthが得られる関数である. 係数が前の式と微妙に違うが, 似たように計算出来よう.
(define (month d) (quotient (+ (* 12 d) 373) 367))
でクリティカルなところを調べるとちゃんと計算出来ている.
0-30 31-60 61-91 92-121 122-152 153-182 183-213 214-244
1 2 3 4 5 6 7 8
245-274 275-305 306-335 336-366
9 10 11 12
やはり3月以降は正しい値と違うので, 補正を先にしてから計算に取り掛かる. 先ほどのR.D.の復活祭は
(gregorian-from-fixed 734601)=>(2012 4 8)
で4月8日と判明した.