Knuth先生のTAOCP第2巻の4.5.4項は素因数に分解する話題である. 最初のアルゴリズム4.5.4Aは2,3,5,...と順に割ってみる方法である. 素数を全部覚えているわけにもいかぬから, 2,3,5のあとは4,2,4,2,...と足して疑似素数を発生する. この辺はもう少し凝れるが, とりあえずはここまで.
その後にあるアルゴリズム4.5.4Cはちょっと面白いので, 今回はその話にしよう. TAOCPによると, この方法は1643年にFermatが使ったものらしい.
分解したい奇数nが与えられた時, このアルゴリズムは下の図の左上のように, 正の整数aとbについて, a2の正方形からb2の正方形を引いた面積をnにするのである. 灰色の部分がnになる.
そういうaとbは, 右上の図のように, aとbの差が1の時, からなず存在する. その隙間の狭い面積をnにするのである. nは奇数だから出来るわけだ. つまりa=(n+1)/2, b=(n-1)/2とすると, a2-b2=(n2+2n+1)/2-(n2-2n+1)/2=4n/4=nである.
このようなaとbが分かれば, n=a2-b2=(a+b)(a-b)だから, a+bとa-bが素因数である. 2つの素因数の差は2b.
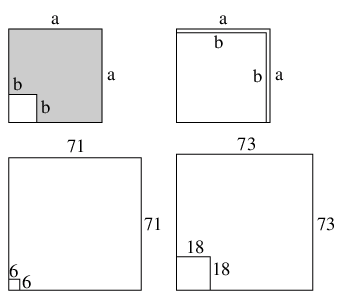
素因数がいくつもあると, aとbの組はいくつもあったりする. n=5005なら下の2つの図のように, 712-62も732-182も5005になる.
求め方はこうだ. 最初a=floor(√n), b=0とする. つまりa2がnに等しいか, ぎりぎりに近いが少し小さ目にする. そしてr=a2-b2を計算し, r<nならaを1増やす. r>nならbを1増やす. r=nならそのaとbが求めるものだ. 素因数を求めるのに割り算をしていない.
たとえばn=9なら, a=3, b=0で決まる. 素因数は3.
n=15ならa=3, b=0, r=9から始め, r<nだからaを4にする. するとr=16になり, r>nだから今度はbを1にする. するとr=15iになり, a=4, b=1に決まる. 素因数は5と3.
n=21ならa=4, b=0, r=16から始める. そろそろ面倒になってきたから, プログラムを書こう.
(define (fermat n)
(define (try a b)
(let ((r (- (* a a) (* b b))))
(display (list a b r)) (newline) ;a,b,rを出力
(cond ((< r n) (try (+ a 1) b))
((= r n) (cons (+ a b) (- a b))) ;素因数が決まる
((> r n) (try a (+ b 1))))))
(try (inexact->exact (floor (sqrt n))) 0))
実行してみると
(fermat 21)
(4 0 16)
(5 0 25)
(5 1 24)
(5 2 21)
=> (7 . 3)
上の図の下の左は
(fermat 5005)
(70 0 4900)
(71 0 5041)
(71 1 5040)
(71 2 5037)
(71 3 5032)
(71 4 5025)
(71 5 5016)
(71 6 5005)
=> (77 . 65)
これで分かるように, このアルゴリズムはaとbの差の大きい方の解を得る.
TAOCPのアルゴリズム4.5.4Cでは, rの計算を加減算だけで出来るように, うえのaとbの代りにx=2a+1, y=2b+1を使い, rもnと比較するのでなく, r-nにして0と比較する.
こういうアルゴリズムだ.
C1 x←2(floor(√n)), y←1, r←floor(√n)2-n.
C2 if r=0,終了 n=((x-y)/2)((x+y-2)/2).
C3 r←r+x, x←x+2.
C4 r←r-y, y←y+2.
C5 if r>0 →C4, else →C2.
(TAOCP風の記述では, C2, C3のような各ステップの終わりに, 行き先(→)の指定がなければ, 次のステップへ進むことが了解されている.)
このプログラムの意外なのは, C2でr=0でなければxとyを増やしてしまう点だ. xを増やした結果はr=0にならなず, r>0になるから, yも同時に増やしている. n=19(素数)でトレースしてみる. 赤字のrはnより小さく, aを増やす時を示す.
(fermat 19)
(4 0 16)
(5 0 25)
(5 1 24)
(5 2 21)
(5 3 16)
(6 3 27)
(6 4 20)
(6 5 11)
(7 5 24)
(7 6 13)
(8 6 28)
(8 7 15)
(9 7 32)
(9 8 17)
(10 8 36)
(10 9 19)
=> (19 . 1)
nが平方数なら, n=9の例のように一発で決る. そうでないなら, aは√nより小さいからr<nになり, aを増やす. その後bを増やすとrは減って, nに等しくなるか(つまり停止するか), r<nになりaを増やす. 先ほどはr>nだったrからb2を引いてr<nになったところへ, bより大きいa2を足すのだから, b2を引くまえのrより大きくなり, r=nとなるはずはないのである. (上の結果の赤字の上下のrの値を見較べると, 下の方が大きいのが分かる.)
前のプログラムも
(define (fermat n)
(define (try a b)
(let ((r (- (* a a) (* b b))))
(display (list a b r)) (newline) ;a,b,rを出力
(cond ((< r n) (try (+ a 1) (+ b 1)))
((= r n) (cons (+ a b) (- a b))) ;素因数が決まる
((> r n) (try a (+ b 1))))))
(try (inexact->exact (floor (sqrt n))) 0))
と改良できて,
(fermat 19)
(4 0 16)
(5 1 24)
(5 2 21)
(5 3 16)
(6 4 20)
(6 5 11)
(7 6 13)
(8 7 15)
(9 8 17)
(10 9 19)
=> (19 . 1)
たしかにこの方がスマートだ.