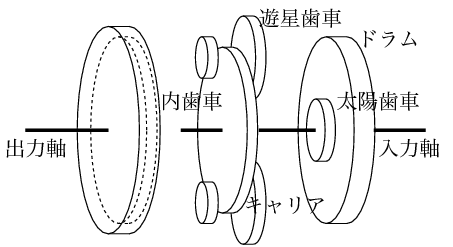
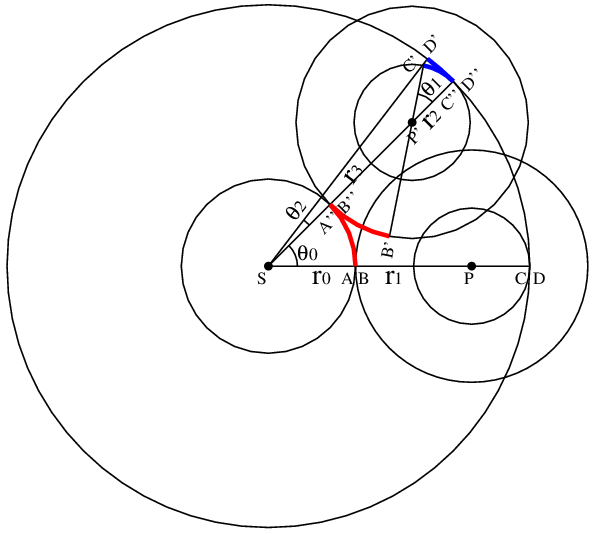
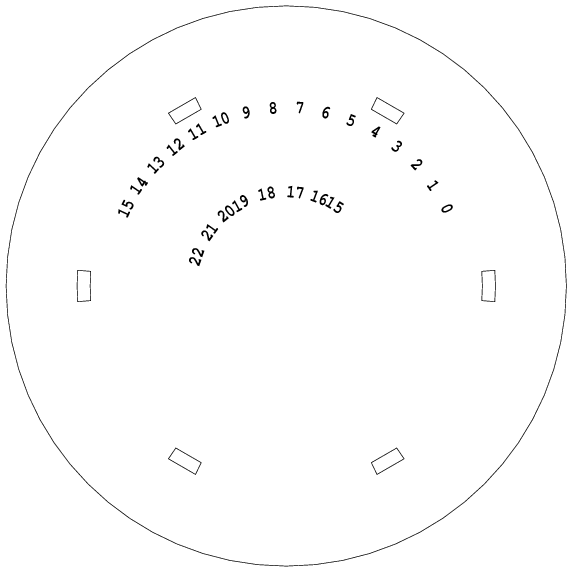
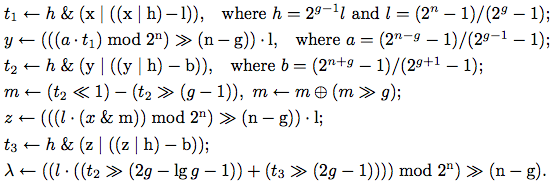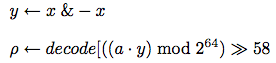最も左のビットの位置を知る法
TACPにはもっと凄いλ関数の計算法がある. 今回はそれを説明しよう.
xのサイズは知らなければならないが, それがどんなに大きくてもbignumのような2adic integer(2個進数)での処理だ.
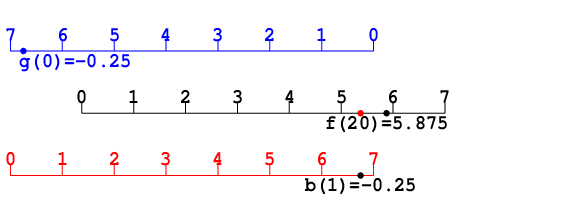
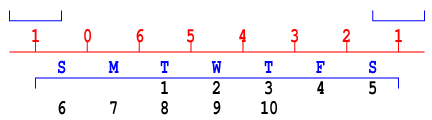
まず準備としてあるアルゴリズムを考える. 具体的に4ビットとしよう. 4ビットだから対象は0≤
x<16 である.
c≤8と最も左のビットだけが1の
h=8が登場する.
h|
x-
cは引かれる方が8≤ <16だから, 0≤
x<16について, 差は8-
c≤ <16-
cの2回繰り返しになる.
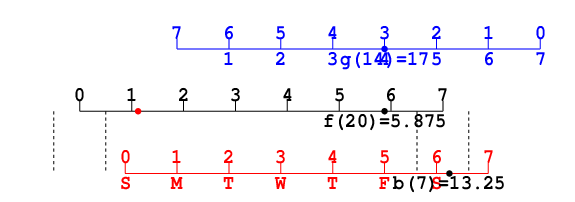
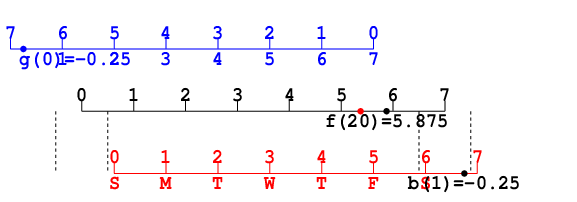
たとえば
c=3とすれば, 5,6,...,12,5,6,...,12になる. つまりそれぞれの最初の
c個だけが<8になる. これに
xをビットごとorすれば, 右半分は
xの最も左のビットが1なので≥8になる. 従って全体では左端の
c個だけが<8, それ以外は≥8になって,
hでビットごとandをとると左端の
c個が0, それ以外は8になる.
c=3の例では0,0,0,8,8,...,8だ. このアルゴリズムで重要なのは, 4ビットの範囲の左から繰下げがないことである.
以下のアルゴリズムにはこれを多用する.
xが如何に大きくても,
gを2の羃,
nを
g2とし,
x<2
nの⌊lg (
x)⌋を計算する.
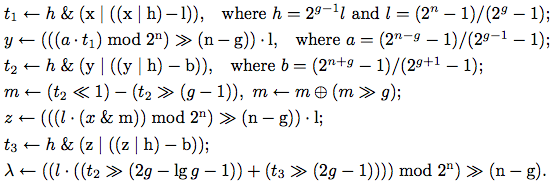
以下の説明では
g=4,
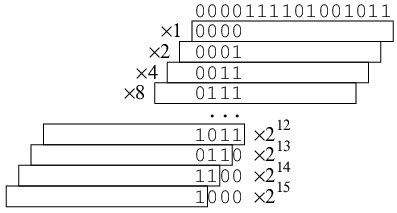
n=16とする. そうすると最初の行にある
lは2
16-1, つまり1111111111111111を2
4-1, つまり1111で割るから0001000100010001になる. 従って
hはそれを3ビット左へシフトした1000100010001000になる.
最初の行は16ビットを4ビットの区間4つのそれぞれについて, 4ビットがオール0かそうでないかを上のアルゴリズムで調べる.
c=1の場合だ.
各区間はその区間がオール0か否かにより, 0か8になる. その結果が
t1だ.
だから
t1は各々の区間の結果をp,q,r,sのビットで表すと, p000q000r000s000になる. p,q,r,sの少なくても1つは1である.
次の行はまず
aを計算する. 2
12-1つまり111111111111を2
3-1つまり111で割るから
a=001001001001である.
これを先ほどの
t1に掛けるから, 積は
p000q000r000s000
p000q000r000s000
p000q000r000s000
p000q000r000s000
の和,
p00pq0pqrpqrsqrs0rs00s000
222221111111111
4321098765432109876543210←ビット位置
になり, この下から12,13,14,15ビットをとるから
yはpqrsに
lを掛けたもの, pqrspqrspqrspqrsになる. 言い換えれば区間の情報を4ビットに詰め込んで4(=g)回コピーしたものが出来た.
今度は
t2の計算だ.
bは2
20-1を2
5-1で割るから
b=1000010000100001となる. だから式中の
bは左端の区間から順に1000, 0100, 0010, 0001で, これらを
cとしてまたあのアルゴリズムを使う.
pqrs≥1000>100>10>1ならすべての区間で8になり,
1000>pqrs≥100>10>1なら0888になり,
1000>100>pqrs≥10>1なら0088になり,
1000>100>10>pqrs≥1なら0008になる.
従って
t2は二進法では
1000100010001000
0000100010001000
0000000010001000
0000000000001000
のいずれかになり, このそれぞれから
mは
1111111111111111
0000111111111111
0000000011111111
0000000000001111
になり, 4ビット右シフトしたものとxorすると
mとして
1111000000000000
0000111100000000
0000000011110000
0000000000001111
が出来る.
次の行は最も左の1を持つ区間を
mでマスクしてとりだし,
lを掛けて左へ4個ならべ16ビットに区切ってから12ビット右シフトして右端の4ビットに置き, さらに
lを掛けて4区間全体に展開する. 先ほどのpqrsから最も左の区間を選んだように, 今度は最も左のビットの位置が
t3に出来る.
整理すると最も左の1のある区間が右端にあれば
t2は0008, その1つ左にあれば0088, 左端の区間なら8888である.
その区間で最も左の1が右端にあれば
t3は0008, 左端にあれば8888である.
これからビットの位置λを計算するにはこうする.
t2を5ビット右シフトするから, 0,4,44,444のいずれかになる.
t3を7ビット右シフトするから, 0,1,11,111のいずれかになる.
これらを上下から取って足し,
lを掛けて12,13,14,15ビット目をとるとそれがλである. たとえば444と1だとすると和は445になり,
445
445
445
445
この4+4+5で13が得られる. 下からの繰り上げはないか心配だが, この計算は十六進であり, 最大の444と111でも5+5+5になって繰り上げはない.
このアルゴリズムは繰り返しがないのでO(1)と書いてあるが, 乗算が5回もあるから実用にはならないとTAOCPはいう.
次はDoループはあるがステップ間のジャンプはないアルゴリズムである.
 d
d=4とすると
n=
d・2
d=64になる. この値を使ってアルゴリズムを調べてみよう.
B1. λ=0とした後, ⌈lg
n⌉=6だから,
k=5,4について
xを32ビット, 16ビットの幅に1があるかどうかで
xを右シフトし, λを増やす. このステップが終わると
xは最も左のビットを含む16ビットの区間になり, その区間がどこにあるかに従ってλは0, 16, 32, 48のいずれかになっている.
B2. 16ビットの区間に縮められた
xを4つの区間にコピーする.
次にμ
d,
kというのがでてくるが, 右から2
kごとに1と0を繰り返す長さ2
dのビット列である.
μ
d,k=(2
2d-1)/(2
2k+1)
今は
d=4だから
μ
4,3=0000000011111111
μ
4,2=0000111100001111
μ
4,1=0011001100110011
μ
4,0=0101010101010101
μ
4,3の0の部分を左半分, 1の部分を右半分といおう. 同様に
μ
4,2の0の部分を左四半分, 1の部分を右四半分といい,
μ
4,1の0の部分を左八半分, 1の部分を右八半分といい,
μ
4,0の0の部分を左十六半分, 1の部分を右十六半分といおう.
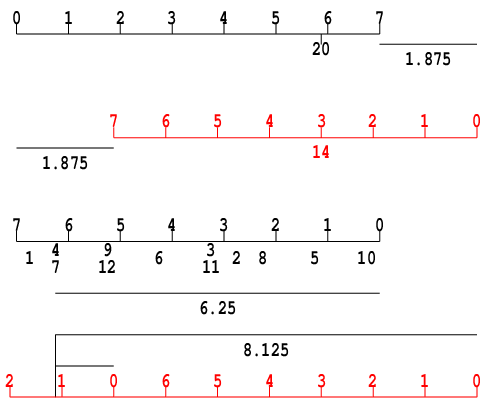
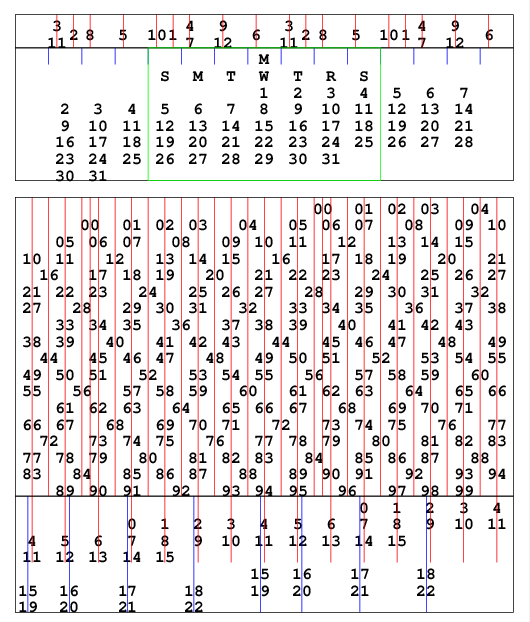
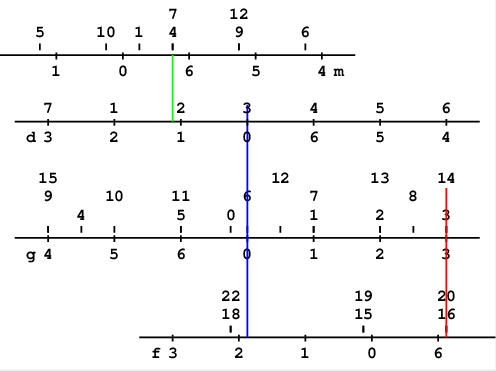
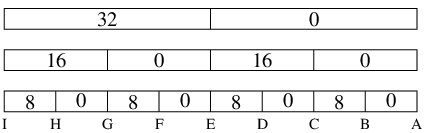
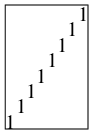
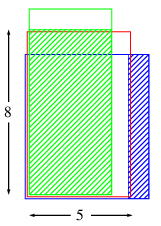
すると下の図で灰色の部分が左なんとか半分, 白い部分が右なんとか半分である.
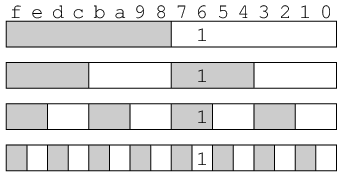
B3. これらのμを繋げてビットごとにnotをとったものと
xのandを
yとする. つまり
xの左なんとか半分の1をとりだす.
B4.
x⊕
yは右なんとか半分の1になるわけだ. そして
h=8000800080008000としておなじみのアルゴリズムを使う.
そうすると左部分をアルゴリズムの
x, 右部分を
cとすることになるので,
x<
cの時に0,
x≥
cの時に8だったように, 左≥右なら0, そうでなければ8000になる.
上の図で最上段の0〜fはビット番号で, そのビット6に最も左の1があるとすると上から順に
左<右
左>右
左>右
左<右
だから, B4の
tはそれぞれの区画で0, 8000, 8000, 0になる.
B5. ⌈lg
d⌉=2なので, 0,1の
kについて
2
4-2
0=15ビット,
2
5-2
1=30ビット
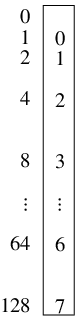
ずつ左シフトして加える. 8の立つビットを左からp,q,r,sとするとそれらのビット位置はそれぞれp=63, q=47, r=31, s=15である.
まず15ビット左へ移るから, qは62, sは30になりpq, rsは並ぶ. それをさらに30ビット左シフトすると31,30にあったrsは61,60になり, pqrsは並ぶ.
2
64の剰余をとるから64ビットレジスタの左端に出来る.
先ほどの例ではその4ビットに0110, つまり最も左のビット位置の6ができる. それを
n-
d=60ビット右シフトし, すでに得られていたλと足すと最も左の1のビット位置が得られるのである.
ところで理解して頂けたであろうか. 私はまずSchemeでプログラムを書いて実行したりして, 様子を見ながらアルゴリズムがどうなっているかを考えた. 分かってしまえば簡単なのだが, 最初に述べたアルゴリズムが何をしているか分からないうちは, なんとも不思議に思うアルゴリズムであった.
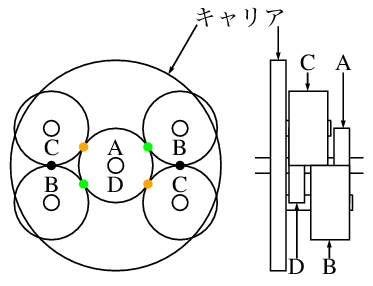
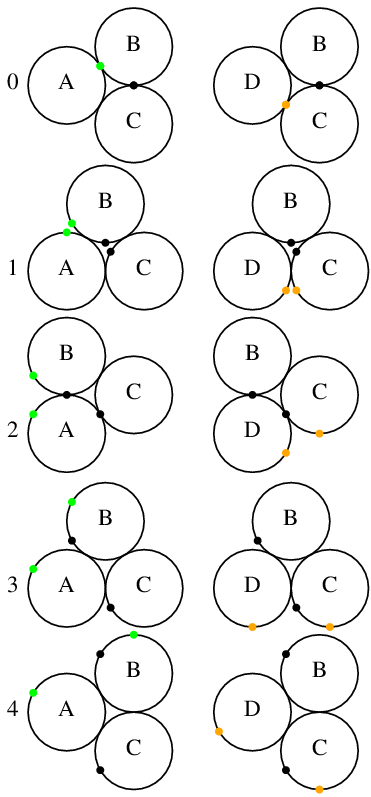



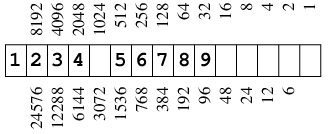 のように出力するには, スペースの位置の下の数と, 最後の桁の上の数を足したものがパラメタの値であり, 28行目は3072+32=3104となっている.
のように出力するには, スペースの位置の下の数と, 最後の桁の上の数を足したものがパラメタの値であり, 28行目は3072+32=3104となっている.