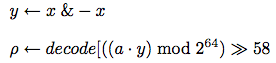最も右のビットの位置を知る法
TAOCP 7.1.3はbitwise tricks and techniques(ビットごとの秘法と技法)で楽しい話題が満載だ. このブログで以前取り上げた
ビットスワップもそこにある.
今回の話は計算機にある語
xの最も右にある1のビットの位置を計算するもので,
x = 0なら1のビットはないから, エラーか不定とするか無限大とするかだが, その辺はどうでもいいので
x≠0 の場合を考える.
xに対してこの位置をρ(
x)で表すので, 位置を求めるアルゴリズムをρ関数という. ρは右(right)のRに対応するギリシア語のアルファベット(小文字)である. これに対し最も左のビットはTAOCPではleftのLのギリシア語のλという. λはLisp屋にはちょっと困る命名だ.
二進法での計算に慣れている人は, 最も右の1のビットを取り出すのが簡単なことは知っている.
x & -
xでそのビットが得られる.
x = 0ならどのビットも立たず0である.
例えば
xが十進法の10なら, 二進法では1010, -10は二進法では ...0110(左の方は1が何桁も並んでいる)だからandをとると...0010となる. 二進法のビットを右からa
0, a
1,...と番号をつけると, ...0010の1はa
1だから位置としては1とする. ρ(10)=1だ.
奇数は右端が1なのでρ(奇数)=0である.
ρ関数は原始的には右端のビットが1になるまで
xを右シフトすればよい.
(define (rho x)
(do ((i 0 (+ i 1))) ((odd? x) i)
(set! x (quotient x 2))))
(map rho (a2b 1 17))
=> (0 1 0 2 0 1 0 3 0 1 0 2 0 1 0 4)
x & -
xで最も右のビットだけが得られたら, その2を底とする対数をとるという方法も考えられる. TAOCPでは2を底とする対数をlgと書くから,
(define (lg x)
(/ (log x) (log 2)))
2の63乗までのlgを取ってみると
(do ((i 0 (+ i 1))) ((= i 64))
(display (lg (expt 2 i))) (newline))
0
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.000000000000004
30.
31.000000000000004
32.
33.
34.
35.
36.
37.
38.
39.00000000000001
40.
41.
42.
43.
44.
45.
46.
47.00000000000001
48.
49.
50.
51.00000000000001
52.
53.
54.
55.00000000000001
56.
57.
58.00000000000001
59.00000000000001
60.
61.
62.00000000000001
63.
ところどころに誤差が出るからroundしinexact->exactすると
(define (rho x)
(inexact->exact (round (/ (log x) (log 2)))))
(map (lambda (i) (rho (expt 2 i))) (a2b 0 64))
=>
(0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62
63)
しかしこれらはアルゴリズムとしてはお粗末で, いろいろな工夫がされている. 例えば語の中の1を数える命令(sideway addition SADD)を計算機が持つているなら,
x & -
xで右端の1だけが取れた後, 1を引くと右端の1は0になり, その右の0は1になるから1の数を数えればよい.
MMIXのSADDはこのためにあるような命令で,
SUBU t,x,1; SADD rho,t,x
SUBU で
xから1を引き, SADDはtのビットが1で, xのビットが0のものの和をとるからrhoに答えが得られる.
x = 0の時は, 1を引くとtがオール1になり, xが0だから64ビットの1が足されて64が得られる. TAOCPにはこれを無限大とみてよいと書いてあった.
SADDのような奇妙な命令がない場合のTAOCPの方法はこうだ.
MMIXというアセンブリ言語で書いてあるがそれを写すと
m0 GREG #5555555555555555 ;m1 GREG #3333333333333333;
m2 GREG #0f0f0f0f0f0f0f0f ;m3 GREG #00ff00ff00ff00ff;
m4 GREG #0000ffff0000ffff ;m5 GREG #0000ffff0000ffff;
NEGU y,x; AND y,x,y; AND q,y,m5; ZSZ rho,q 32;
AND q,y,m4; ADD t,rho,16; CSZ rho,q,t;
AND q,y,m3; ADD t,rho,8; CSZ rho,q,t;
AND q,y,m2; ADD t,rho,4; CSZ rho,q,t;
AND q,y,m1; ADD t,rho,2; CSZ rho,q,t;
AND q,y,m0; ADD t,rho,1; CSZ rho,q,t;
最初の3行はマスク用の定数である. GREGは大域レジスタを設定する命令でm0というラベルの場所を十六進(#で示す)の5555555555555555にするというような命令が並ぶ.
1行目の中程「 ;m1 」のセミコロンの次にすぐm1が続いているのは, m1をラベルにしたいからである. 4行目から命令の前に空白があるのは, ラベルがないことを示す. 行頭やセミコロンの直後に文字があるとラベルに扱われる.
さて命令の部分に入って, NEGU y,x; はxのunsigned negativeをとってyに入れる. AND y,x,y;はx & -xを作ってそれをyとした. yには最も右の1のビットだけが立っている.
AND q,y,m5; はyのビットが64ビットの左半分にあればqが0になり, 右半分にあれば, yのままの場所に1が残る.
ZSZ rho,q,32; はzero or set if zeroで, qが0ならrhoに32を入れ, そうでないなら0を入れる. 従ってyのビットが左半分にあればrhoは32になる.
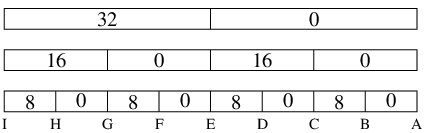
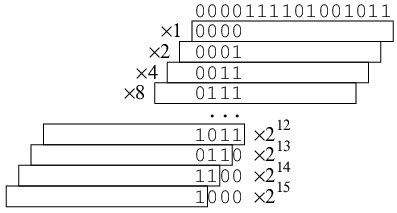
次の行はm4のマスクで調べ, 以前のrhoに一応16を足したものをtに用意した上で, 上の図の16の範囲にあれば前のrhoにtを入れる. CSZは条件付きでqが0ならtをrhoに入れるが, そうでないなら何もしない.
そういう次第で, 上の図の上の2段目の区画のどこにyのビットがあるかでrhoに0, 16, 32, 48 のいずれかが入る.
同様にして8ビットごとの区間のどこにあるかでrhoに8を足す足さないとしてyのある区画を決める.
後も同様で, 変数rhoには答えの位置の番号が入るのである.
TAOCPのこのアルゴリズムの後にはまだ何か書いてある. 「最後の3行を
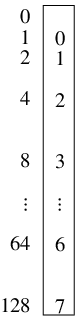
SRU y,y,rho; LDB t,rhotab,y; ADD rho,rho,t;
としてもよい. rhotabは129バイトの表(その8個だけを使う)の原点である.」 これは何か.
最後の3行に来たときにはyのビットは上の図の最下段のどれかの8ビットの区画にあり, その右端のビット位置がrhoに入っている. 従ってyを右にrhoビットシフトすると, yのビットは右端の8ビットの区画に移動する.
つまり
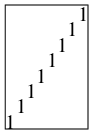
のどれかになっている. この一番上なら(1なら)0, その次なら(2なら)1, 4なら2, ..., 128なら7をrhoに足せばよい. 従って次のような表を用意すればよいわけである. たしかに129の場所があり, そのうち8カ所だけを使っている.
MIT Schemeのbit-stringを使って実装してみた.
(define (bmake x) (signed-integer->bit-string 64 x))
(define (band x y) (bit-string-and x y))
(define (bzero? x) (bit-string-zero? x))
(define m0 (bmake #x5555555555555555))
(define m1 (bmake #x3333333333333333))
(define m2 (bmake #x0f0f0f0f0f0f0f0f))
(define m3 (bmake #x00ff00ff00ff00ff))
(define m4 (bmake #x0000ffff0000ffff))
(define m5 (bmake #x00000000ffffffff))
(define (rho x)
(let ((bx (bmake x)) (by (bmake (- x))) (bq 0) (rho 0) (t 0))
(set! by (band bx by))
(set! bq (band by m5))
(set! rho (if (bzero? bq) 32 0))
(set! bq (band by m4))
(set! t (+ rho 16))
(if (bzero? bq) (set! rho t))
(set! bq (band by m3))
(set! t (+ rho 8))
(if (bzero? bq) (set! rho t))
(set! bq (band by m2))
(set! t (+ rho 4))
(if (bzero? bq) (set! rho t))
(set! bq (band by m1))
(set! t (+ rho 2))
(if (bzero? bq) (set! rho t))
(set! bq (band by m0))
(set! t (+ rho 1))
(if (bzero? bq) (set! rho t))
rho))
(rho 1000)=>3
(rho 10000)=>4
(rho (+ (expt 2 62) (expt 2 32)))=>32
≥2
63ではbit-stringを作るところでエラーになったが, 他はうまくいっている.