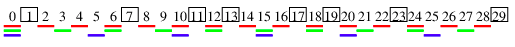TAOCPの素因数探しの最初のアルゴリズム4.5.4Aは, 2,3,...と素数で次々を割ってみるやつだ.
A1. t←0, k←0, n←N.
A2. if n=1, 終了.
A3. q←floor(n/dk), r←n mod dk.
A4. if r≠0 →A6.
A5. t←t+1, pt←dk, n←q, →A2.
A6. if q>dk, (k←k+1, →A3).
A7. t←t+1, pt←n, 終了.
ここでd
0=2,d
1=3, ....は割ってみるべき, 次々の素数で, d
2=5の次は, 2,4,2,4,...と足していくという方法があるとこのアルゴリズムには書いてある. つまり, d=2,3,5,7,11,13,17,19,23,25,29,31,35,...とする. これをみると, 25,35以外は素数で, 一見うまく行きそうだが, 要するに2と3で割れない数を仮に素数としている. 多くの素数を記憶するわけにはいかぬので, 疑似素数列を生成するわけだ.
上のプログラムをSchemeでコーディングしてみる. p
tは素因数の列の配列なので, Schemeではリストpにする. A5とA7でtを1増やすのは, 配列pの添字を進めるので, リストではいらない.
t←t+1, pt←nは
(set! p (cons n p))となる. kは約数の配列の添字だ. A6でkを増やすのは次の約数にするのだから, ここは
(nextd)として, 後で考える.
(define (a2) (if (= n 1) p (a3)))
(define (a3) (set! q (quotient n d))
(set! r (modulo n d)) (a4))
(define (a4) (if (not (= r 0)) (a6) (a5)))
(define (a5) (set! p (cons d p)) (set! n q) (a2))
(define (a6) (if (> q d) (begin (nextd) (a3)) (a7)))
(define (a7) (cons n p))
a4の
(not (= r 0))は
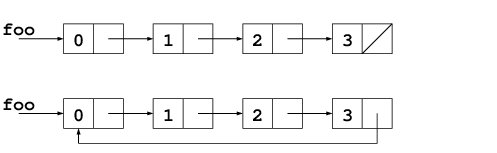
(> r 0)でよいが, その辺にはこだわらぬ. dは初期値を2とし, 1,2,2,4と順に足せば3,5,7,11が得られる. そこでこのリスト
(1 2 2 4)の最後を
(...2 ^ 2...)の間の ^ のところに繋げれば無限リスト
(1 2 2 4 2 4 2 4 ...)が作れて, その後も2,4,2,4と足せるはずだ. このリストを
ddといおう. 次のようにして作る.
(define dd '(1 2 2 4))
(set-cdr! (list-tail dd 3) (cddr dd))
そうすれば,
(nextd)は
(define (nextd)
(set! d (+ d (car dd))) (set! dd (cdr dd)))
でよい.
その上と下に
(define (algorithm454a n)
(let ((p '()) (d 2) (q 0) (r 0))
と
(a2)))
をつければ完成で,
(algorithm454a 3628800)でよべば,
(7 5 5 3 3 3 3 2 2 2 2 2 2 2 2)が得られる.
このプログラムでは, 1をfactorizeしようとすると, a2でいきなり止り, 空リストが返る. TAOCPを読み直すと, 「every positive integer n」は p
kを素数, p
1 ≤ p
2 ≤...≤ p
tとして,
n=p1p2...pt
のように一意に表わせる. n=1の時はt=0で成り立つ とあるので, 空リストは当然だ. n=0ならどうか. 0をpositive integerとするかどうかだが, 上のプログラムは止らない.
ところで, 50年も前, パラメトロン計算機でこういう計算をしたころ, 疑似素数列に現れる非素数を, 我々は臨時素数と呼んでいた.
2,4,2,4と足すということは, 6の幅の間に2つの数をテストするから, 疑似素数の全整数に対する頻度は1/3=0.333...である.
2と3と5で割れない疑似素数列なら, その頻度はどうなるか. TAOCPは, 計算時間は20%節約になると説明する.
0から2,3,5のLCM, 30の前までで, 29までで, 2でも3でも5でも割れない数は, 1,7,11,13,17,19,23,29の8個なので, 8/30=0.266... . これが1/3の何%かを計算すると, (8/30)/(1/3)=8/10だから, 計算時間は80%になり, 20%の節約になる.
ついでに, TAOCPに7までにすると, さらに14%節約とあるのを確認しよう.
2*3*5*7=210個のうち, 2でも3でも5でも7でも割れないものは,
(filter (lambda (n) (> (* (modulo n 2) (modulo n 3)
(modulo n 5) (modulo n 7)) 0)) (a2b 0 (* 2 3 5 7))) =>
(1 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79
83 89 97 101 103 107 109 113 121 127 131 137 139 143 149
151 157 163 167 169 173 179 181 187 191 193 197 199 209)
このリストのlengthは48なので, 頻度は48/210. (48/210)/(8/30)=6/7=0.857... これを0.86と思えばTAOCPのいうように節約は14%である.
ところで, 2でも3でも5でも割れない数は, 0から29までに8個あると上に述べた. 計算方法はこうだ. 0から29までの数を書き, 2で割れるもの, 3で割れるもの, 5でわれるものに印をつけると図のようになる.
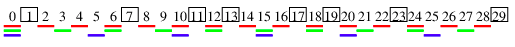
2で割れる15個の数には赤線を引いた. 3の10個は緑で, 5の6個は青である. これらを30から引くと, 30 - 15 - 10 - 6=-1. 6や10のように2重線のものは, 2回引いたから, 実は引きすぎである. これは1回ずつ戻さなければならない. それは6で割れる0,6,12,18,24の(30/6=)5個, 10で割れる0,10,20の(30/10=)3個, 15で割れる0と15の(30/15=)2個で, -1+5+3+2=9になる. しかし, 0は今度は3回戻されてしまった. ここは本来は1回引く場所であるが, -3+3をやってしまった. そこで(30/30=)1回を引いて, 結局四角で囲んだ8個が残る.
こういう計算法をprinciple of inclusion and exclusionという. 日本語では包除原理とか和積の原理とかいうらしい.
この原理により, 2,3,5,7,11までの頻度を計算してみよう.
(define t (* 2 3 5 7 11))
t=>2310
(- t
(+ (/ t 2) (/ t 3) (/ t 5) (/ t 7) (/ t 11))
(- (+ (/ t 2 3) (/ t 2 5) (/ t 2 7) (/ t 2 11) (/ t 3 5)
(/ t 3 7) (/ t 3 11) (/ t 5 7) (/ t 5 11) (/ t 7 11)))
(+ (/ t 2 3 5) (/ t 2 3 7) (/ t 2 3 11) (/ t 2 5 7)
(/ t 2 5 11) (/ t 2 7 11) (/ t 3 5 7) (/ t 3 5 11)
(/ t 3 7 11) (/ t 5 7 11))
(- (+ (/ t 2 3 5 7) (/ t 2 3 5 11) (/ t 2 3 7 11)
(/ t 2 5 7 11) (/ t 3 5 7 11)))
(+ (/ t 2 3 5 7 11)))
=> 480
(/ 480 2310)=>16/17=.20779...
大体1/5である.
上に書いたSchemeのプログラムは, dやpの列をリストにした以外はTAOCPのプログラムの焼き直しである. もう少しSchemeらしくしたのが, 次のプログラムだ.
(define (factor n)
(define dd '(1 2 2 4))
(set-cdr! (list-tail dd 3) (cddr dd))
(define (loop n d p)
(define (nextd)
(set! d (+ d (car dd))) (set! dd (cdr dd)))
(define (next)
(let ((q (quotient n d)))
(cond ((= (modulo n d) 0) (loop q d (cons d p)))
((> q d) (nextd) (next))
(else (cons n p)))))
(if (= n 1) p (next)))
(loop n 2 '()))
(map factor (a2b 1 30))
=> (() (2) (3) (2 2) (5) (3 2) (7) (2 2 2) (3 3) (5 2) (11)
(3 2 2) (13) (7 2) (5 3) (2 2 2 2) (17) (3 3 2) (19) (5 2 2)
(7 3) (11 2) (23) (3 2 2 2) (5 5) (13 2) (3 3 3) (7 2 2) (29))
プログラムは本質的にループだから, loopというプログラムを末尾再帰で呼ぶことにする. ある約数dで割れなければ, 次の約数を(nextd)で準備し, nextを呼ぶ. 素因数分解のたびにddを作り直すのも癪だが, そう長くはないから我慢する. さらに多くの素数の倍数をスキップするddの作り方については, またいつか書こう.