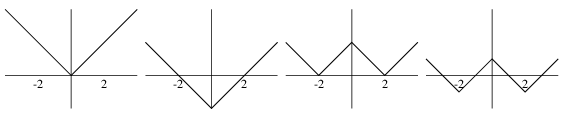
この式の構造はこうなっている. 11行目の(1/2)*に掛けられる因子は4つの項で出来ている.
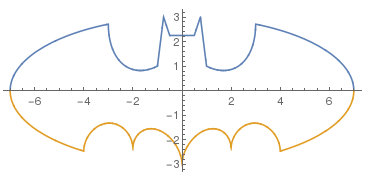
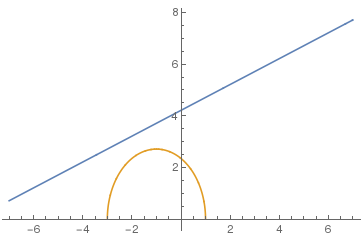
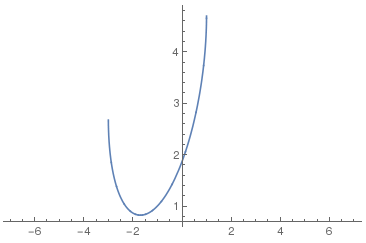
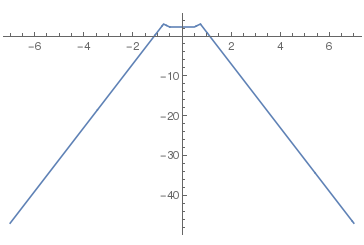
3*Sqrt[1-(x/7)^2] (楕円) +Sqrt[1-(Abs[Abs[x]-2]-1)^2] (4つの小楕円) +Abs[x/2] (折線) -((3*Sqrt[33]-7)/112)*x^2 (放物線) -3最初はお馴染の楕円で高さは3にしてある. 次が4個の楕円で高さはどれも1だ. その次が(0,0)で折り返す直線で, 最後がx2の抛物線である.
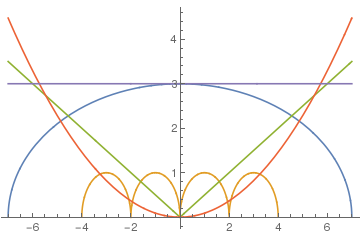
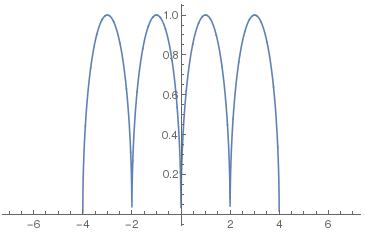
4個の楕円はx=-4,-2,0,2,4の5個所でy=0である. このうち中央のx=0では, 他の項の楕円の3を足し, 最後の3を引き, 折線と放物線はx=0で0だから, 0のままである.
x=4では楕円は3√33/7, 折線は2, 放物線は16*(3√33-7)/112, それから3を引くが, これは計算すると結局0になる.
x=2のところは面倒になったので, Schemeで計算した.
(define (a x)
(define (sq x) (* x x))
(+ (* 3 (sqrt (- 1 (sq (/ x 7)))))
(abs (/ x 2))
(- (* (/ (- (* 3 (sqrt 33)) 7) 112) (sq x)))
(- 3)))
(a 2) => .5094556875135123
(a 3) => .3881737849967646
(a 1) => .3778577420858067
という次第で, 0,±4では0, ±2では0.5くらいになる. 1と3では1.37程度になろうか.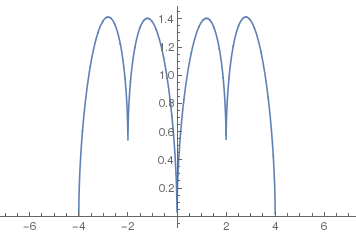
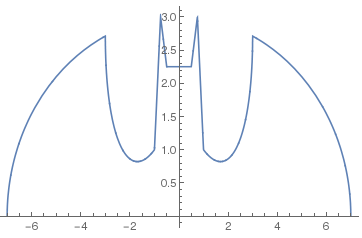
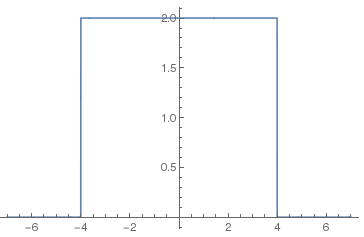
この図を見ると高さの値は微妙に違うようだが, まぁいいか. この図では±4の外側では定義されていないということで, 青線がないが, 前回のフィルタを掛けた下の図では
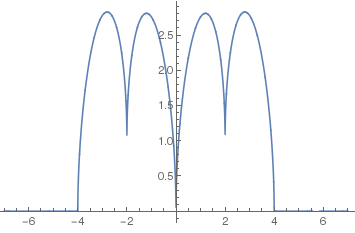
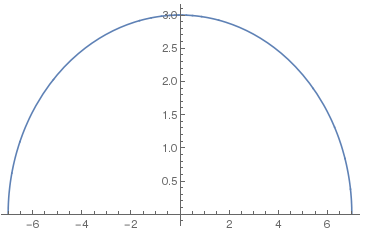
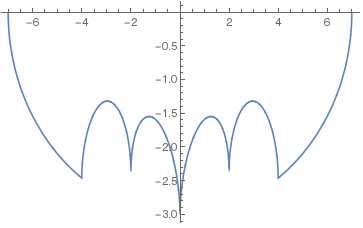
のように外側の方もよくみるとx軸上に青の線が見える. 高さも2倍になっているのが分かる. これから楕円の下半分を引くと, 思ったとおりの下の曲線が出来る.
ところでこの下の図は, 前回のこうもりの絵とはすこし違っている. 最後のAspectRatio->Automaticをつけなかったのである.
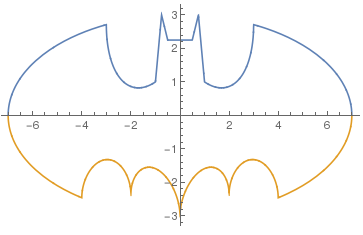
AspectRatioの詳細はまだわからないが, Plot関数では, AspectRatio->Automatic がないと縦横比が黄金比のφになるらしい.
ディスプレイ上で測ってみると, 左右は56ミリ, 上下は33ミリであった.
(/ 56. 33) => 1.696969696969697確かに黄金比に近いといえなくはない. x軸の0から2と, y軸の0から2の長さは明らかに違う. Automaticを指定した前回のこうもりの絵では, 横:縦は正しく7:3になっている.
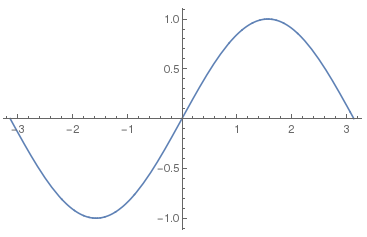
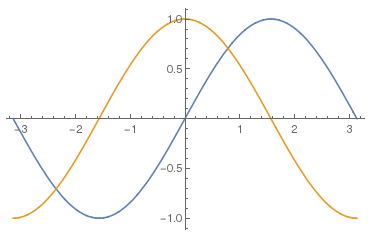
黄金比にするような見栄えを工夫するのがAutomaticの機能のように思うのだが, Mathematicaの文化はこういうものか. 前回のSinの図でも, Automaticがないので, 横/縦は1.7くらい. Automaticを追加すると, 縦と横の長さは1:1になり, もっと平べったい, 正確になった. (世の中のSinカーブでは, 前回の図も含めてx=0での勾配が1になっていない図がかなり多い.)