その1ヶ月ほど前に, 一松信先生の「正多面体を解く」を買ったのだが紙袋にいれたままオフィスに忘れていた.
この書の最後の方に星形正多面体の話題があった. そういえば以前正多面体や準正多面体をいろいろ描いたが, 星形は手つかずであったので早速その部分を読む. 申し訳ないが一松先生の本の図はどうもいまいち分かりにくいのである. やはりこの際, 自分で描いてみるか.
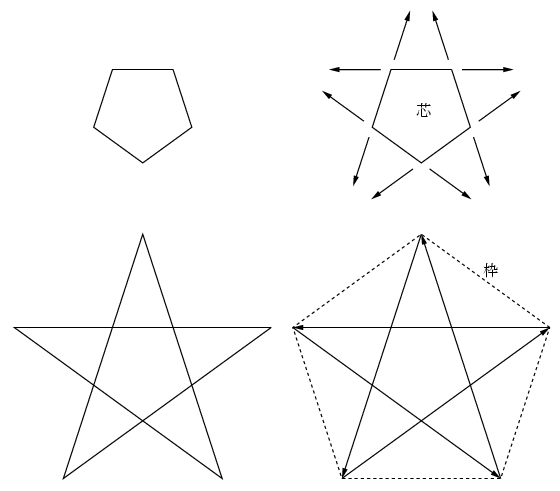
一松先生の受け売りだが, 2次元の星形正多角形(上の図の左下)の書き方には2通りある. 右上のように「芯」の正多角形の各辺を延長すると左下が出来る. あるいは右下の「枠」となる正多角形の頂点をいくつか置きに結ぶ.
星形正多角形は, 普通の正多角形とは違って見えるが, すべての辺の長さが等しく, すべての頂点の角度も等しいから, やはり正多角形である. この図の星形正多角形は正5/2角形というらしい.
立体の手始めは星形小十二面体である. これは正十二面体を芯とし, その各面を延長する.
2010年6月1日の私のブログの
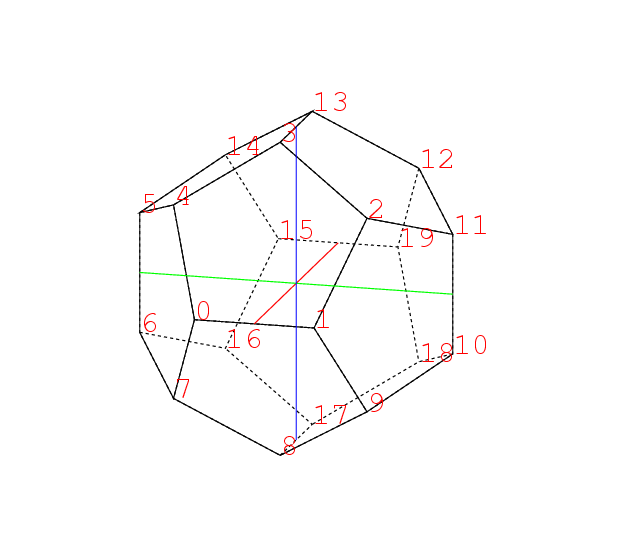
正十二面体を芯とし, そのプログラムの修正て始めよう.
この正十二面体の正面左上を向いている面(頂点が0, 1, 2, 3, 4の面)に隣接する5枚の面を延長すると点20で合わさった五角錐になり
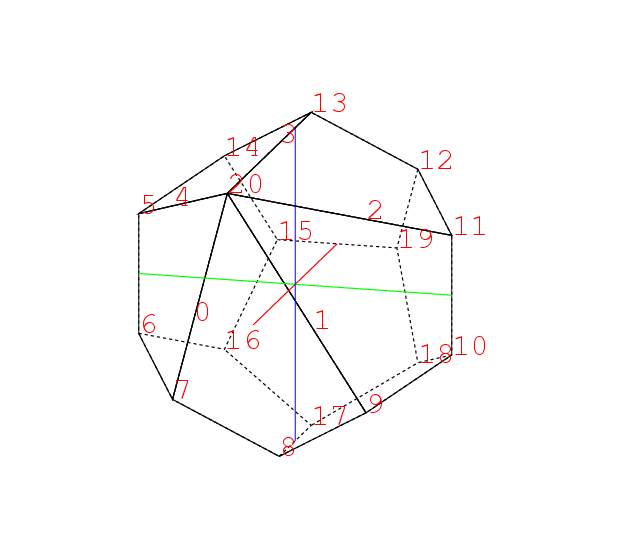
が出来る. この操作を他の11枚の面についても行うと
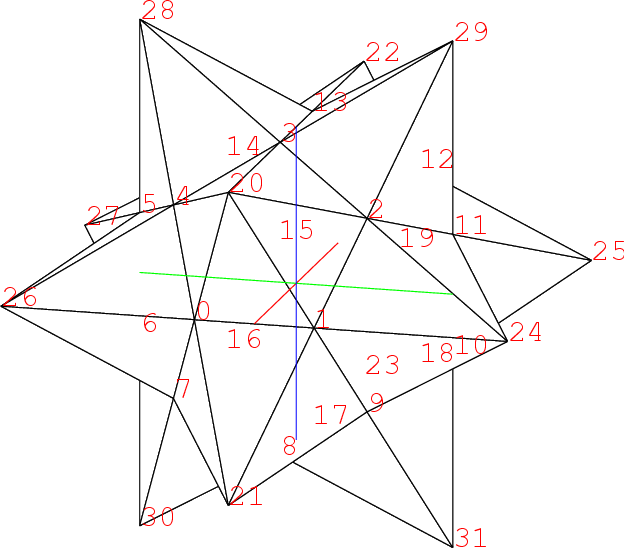
が描ける.
五角錐の頂点の座標は下の図のように得られる.
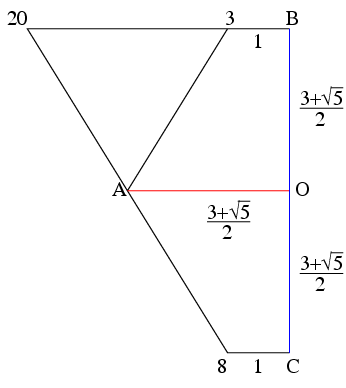
最初の正十二面体で立体を貫くの赤, 緑, 青はx軸, y軸, z軸である. 上の図は立体のzx面の断面である. Aは0と1の, Bは3と13の, Cは8と17の中点で, Oは立体の中心だ.
点20は辺3, 13の延長線上にあり, 立体の辺(稜)の長さの半分を1とすると, OA=OB=OC=(3+√5)/2からx座標が2+√5である.
さて, 星形小十二面体を眺めると, 面0, 1, 2, 3, 4を延長した面28, 21, 29, 26, 24は正5/2角形である. こういう形が12枚あるわけだ. 芯の正十二面体の12の面に五角錐を載せたから, 頂点も12ある. 辺は各頂点から5本出ているが, 相棒の頂点と共有だから都合30本になる.
例のEulerの公式は 面+頂点=辺+2だが, 12+12≠30+2で公式が成り立たないという. 「正多面体を解く」にはちゃんと説明があるが, 受け売りになるので省略.
さてもう1回似たような図を示す.
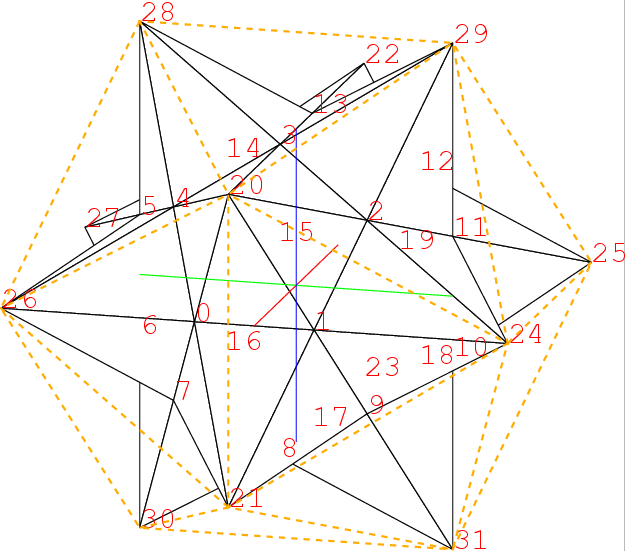
このオレンジ色の破線は星形正多面体の枠の正二十面体である. 平面だと, 頂点をいくつか置きに辿るといえるが, 立体の場合はどういえばいいだろうか.
一方, 星形小十二面体の隠面消去だが, 五角錐を構成する三角形を遠方にある物から並べ, 各三角形を描画する際, まず内側を白で塗りつぶしてから黒で輪郭を描いた.
始めの正十二面体では, 各面の法線方向を計算し, それと視線の角度を計算して面の見える/見えぬを決めている.

0 件のコメント:
コメントを投稿