一松先生に記述はこうだ「正二十面体の各面に対し, 各辺に隣る三角形の頂点3個を結ぶ正三角形20個を面にとります.」 相変わらず簡潔だ. 面は20, 辺は3×20÷2=30, 頂点は3×20÷5=12. 後に判明するように, 頂点で面は星形(5/2角形)で交わるから, Schläfliの記号は{3,5/2}. いやはや記述とは反対に大変な難物であった.
前回のブログにあった枠になる正二十面体の図をもう一度示すと.
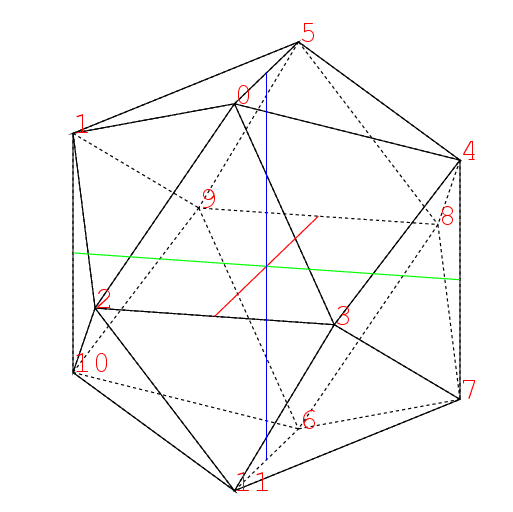つまり頂点0,1,2の面に対しては, それに隣る三角形の頂点5,10,3の三角形で, こういう面だけで出来る立体はそう容易には想像出来ない. 数学者の想像力にはいつもながら脱帽だ. かなりの日時をかけ, 苦心惨憺, 紆余曲折, といいつつも十分楽しんだ末, 出来た図はこれだ. 自画自賛すれば実にもっともらしい.
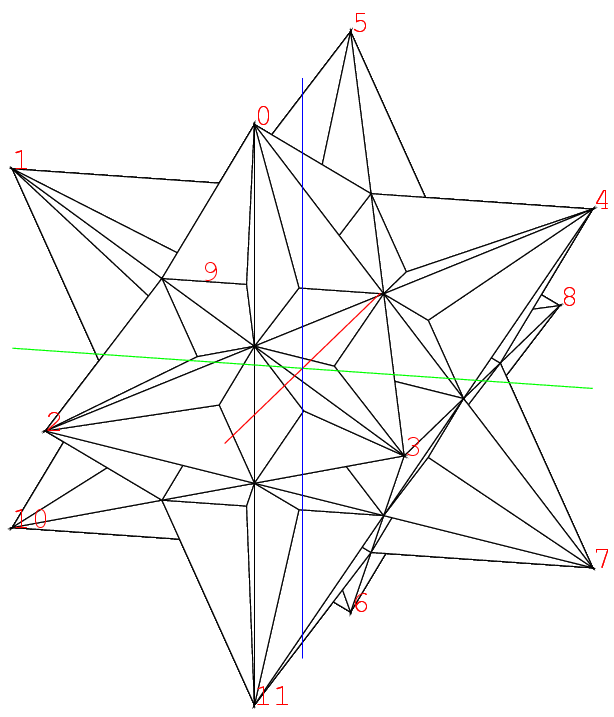たしかに頂点5,10,3を結ぶ三角形は見える. 下は左が正二十面体の面, 右がそれに対応する大きい三角形である.
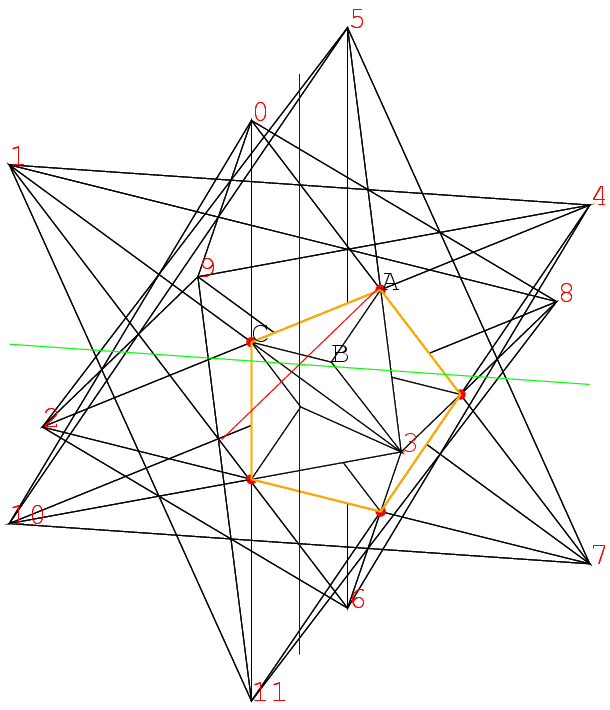
[2 1 0] [10 5 3] [3 2 0] [11 1 4] [4 3 0] [7 2 5] [5 4 0] [8 3 1] [1 5 0] [9 4 2] [2 10 1] [11 9 0] [11 10 2] [6 1 3] [3 11 2] [7 10 0] [7 11 3] [6 2 4] [4 7 3] [8 11 0] [8 7 4] [6 3 5] [5 8 4] [9 7 0] [9 8 5] [6 4 1] [1 9 5] [10 8 0] [10 9 1] [6 5 2] [7 8 6] [4 9 11] [8 9 6] [5 10 7] [9 10 6] [1 11 8] [10 11 6] [2 7 9] [11 7 6] [3 8 10]ためつすがめつ眺めているうちに, これは下の図のオレンジ色の正五角形の上に, 背の高い星形が乗っている; その正五角形が芯になる正十二面体であるらしいと分かって来た.
しかし頂点3に関わる部分だけで三角形は15もある. 都合180個の三角形の座標を計算しなければならぬ. 当然その計算の部分はSchemeで別にやることにした.星形の底面の凸の点は, 例えばAは頂点3と5の線上にあるから, 後で計算出来るとして, 凹の点Bはどうするか. 頂点3からの三角形の辺は, 8,5,1,10,6に向かい, それらの頂点は8,1,6,5,10の順に星形(5/2角形)につながっている.
ABの線は頂点5, 10の線と平行であり, BCの線は頂点8, 1の線と平行なので, その交点の座標を知る必要がある. このような交点を5個計算し, 3と5の位置を内分してAが得られたように, 3と交点を同じ比で内分するとBが得られるわけだ. この比は1:(1+√5)/2なので, 黄金分割であった.
180個のすべての三角形の頂点の座標が得られてから, それらの各点の視線方向の距離を計算し, 遠い物から順に描くと最初の図が出来た.
一応目的は達成したが, こういう水の溜まる立体を白地で示すと, どこが凸でどこが凹かが分かりにくい. 次は面を濃淡に塗り分けてみたい.
0 件のコメント:
コメントを投稿