多面体描画道楽

Archimedes多面体というのがある. 切頭八面体とか切頭二十面体とかはその仲間だ. その中に, 斜方二十・十二面体という長い名前のものがあった. 英語ではrhomb icosi dodecahedronという. rhombが斜方, icosiが二十, dodecaが十二, hedronが面体の単数だ.

これば難しそうだ. 図面を何日も眺めたが, アタックの入口が見つからない. 空しく過しているうちに, やっと解決の糸口が見えてきた. 次の図で説明しよう.



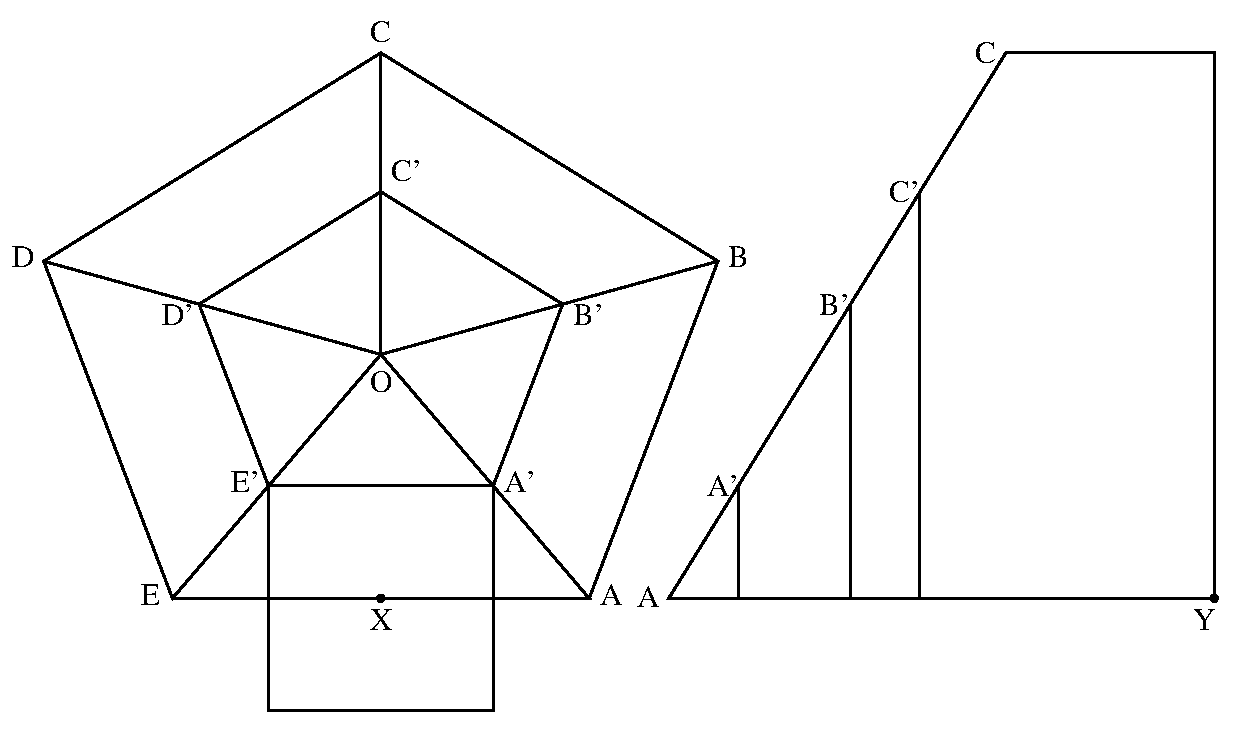
左は正十二面体をx軸方向から見たもので, 真下のXと書いた上の点がX軸である. 右はそれをy軸方向から見た図である.

斜方二十・十二面体には, 五角形が12, 四角形が30, 三角形が20ある. 一方, その元になる正十二面体は, 面Fが12, 頂点VがHamiltonianの巡礼で分かるように20, 辺Eが30ある. Eulerの式 V+F=E+2である.

つまり, 五角形は面が, 四角形は辺が, 三角形は頂点に対応している.

正十二面体の頂点は, 3つの面が合わさっているから, それを削っていけば, 三角形が現れるが, それでは五角形が十角形になる切頭十二面体が出来るだけである.

下の左の図で, 正五角形ABCDE(面が傾いているから, 上下がつぶれて見える)を中心に向って縮小すると, 下の辺と下にある五角形の対応する辺で作る四角形が正方形になる時点があるはずで, その時, 同じ辺の長さを持つ正五角形A'B'C'D'E'と正方形が出来る.

というわけで, A', B', C', D', E'の右方向へのy座標と, 上方向のz座標が計算出来る. 各点のz座標が分かると, 右の図のようにして, x座標も決る.

AEの距離を2とした時, A',B',C'の座標は次の通りである.



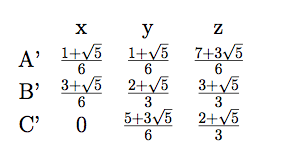
こうして描いた多面体は次の通り.



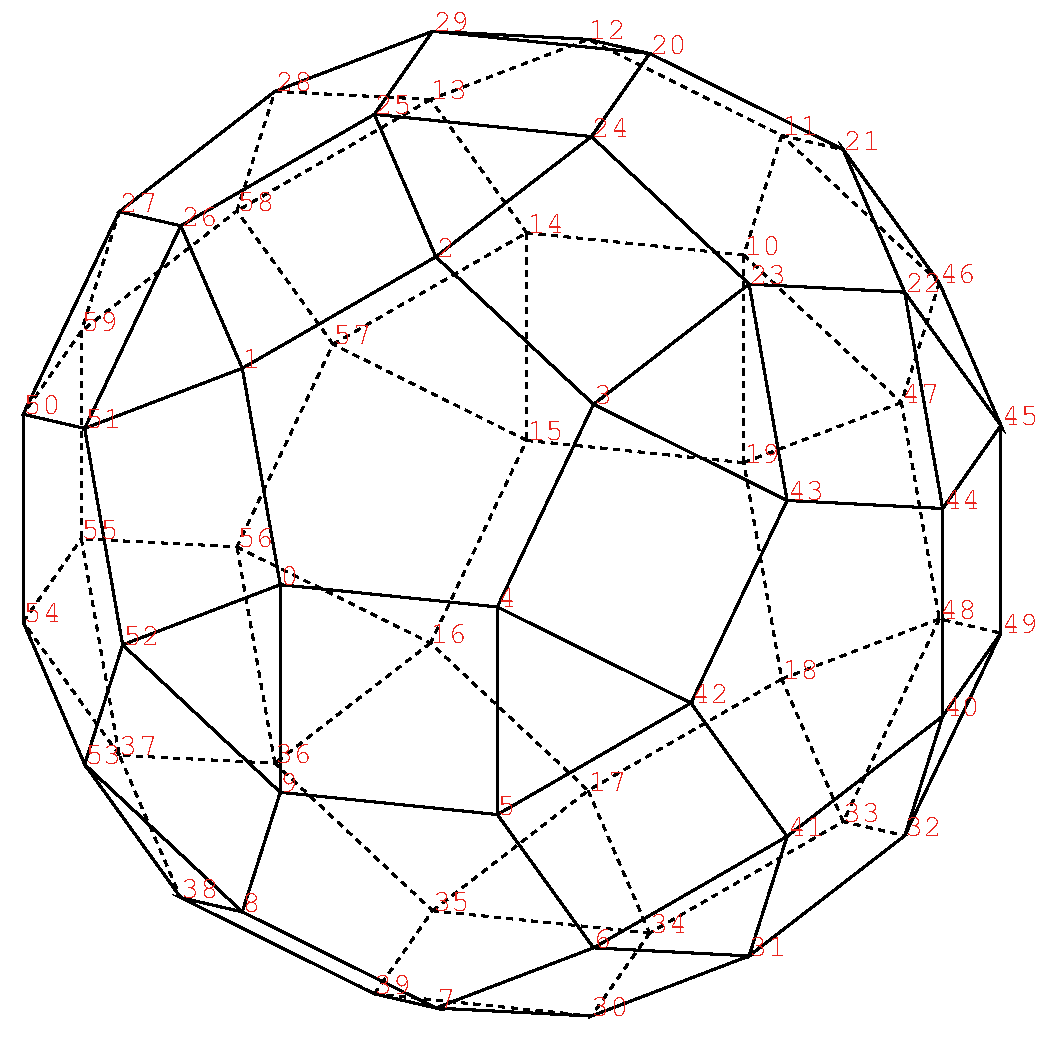
もっともらしいではないか.