Gaussの正十七角形

高木先生の近世数学史談に, 19歳のGaussが, 1796年3月30日の朝, 正17角形の描き方に気づいた話が出ていることは, すでにこのブログで述べた(2008年12月12日). 今回はその計算を追ってみたい.

360°=17φ とおく. また,

cos φ+cos 4φ=a
cos 2φ+cos 8φ=b
cos 3φ+cos 5φ=c
cos 6φ+cos 7φ=d
a+b=e
c+d=f

とする. 「よく知られているように」 e+f=-1/2 (「...」内は高木先生)

ここでまず え? と思う. 計算してみると,

(define pi (* 4 (atan 1)))
(apply + (map (lambda (n) (cos (* n (/ (* 2 pi) 17))))
  (a2b 1 9)))
=> -.4999999999999999

(いつものように(a2b m n)は[m .. n)を生成する.)



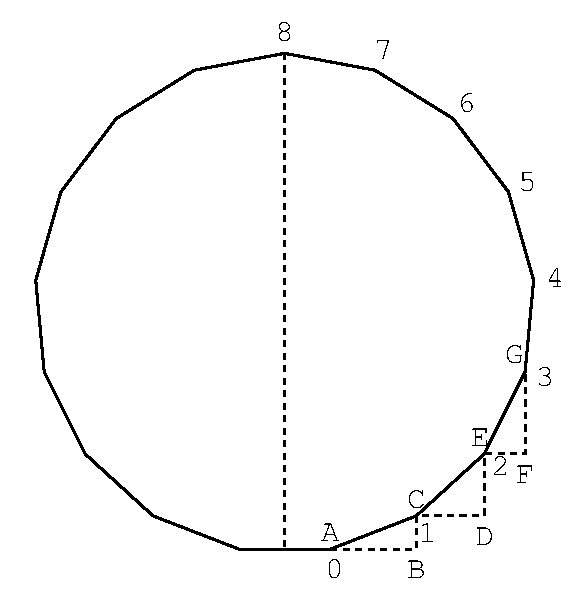
しかし, この図をみれば, 1辺の長さ1の正17角形の1辺の半分だから, 当然な話だ. つまり, 角CABは正17角形の外角なので, これがφ. 従って多角形の1辺を1とすると, ABがcos φ, CDがcos 2φ, EFがcos 3φ,... . cos 8φまでいくと, 頂点の8までの横軸の和になり, これはAからみれば-1/2なのは明らか. 一旦そうと分かると, よく知られているとも思える.^^)


「con nφ=cos(17-n)φに注意し, 簡単な計算によって」
2ab=e+f=-1/2
2ac=2a+b+d
2ad=b+c+2d
2bc=a+2c+d
2bd=a+2b+c
2cd=e+f=-1/2

これはなぜか. 正直に掛けてみる.
2ab=2(cos φ+cos 4φ)*(cos 2φ+cos 8φ)
=2cos φ*cos 2φ+2cos φ*cos 8φ+2cos 4φ*cos 2φ+2cos 4φ*cos 8φ.

三角法の公式を見ると,
cosα+cosβ=2 cos(α+β)/2*cos(α-β)/2
というのがあり, cosの積を和に出来る. これを使うとm>nとして,
2cos mφ*cos nφ=cos(m+n)φ+cos(m-n)φ
だから

2cos φ*cos 2φ=cos 3φ+cos φ
2cos φ*cos 8φ=cos 8φ+cos 7φ
2cos 4φ*cos 2φ=cos 6φ+cos 2φ
2cos 4φ*cos 8φ=cos 5φ+cos 4φ
と1から8までそろうから, e+fになる.

これを6回もやるのは面倒だから,

(define a '(1 4))
(define b '(2 8))
(define c '(3 5))
(define d '(6 7))
(define (foo m n) (list (min (+ m n) (- 17 m n))
  (abs (- m n))))
(define (prod x y)
 (sort (append (foo (car x) (car y)) (foo (car x) (cadr y))
  (foo (cadr x) (car y)) (foo (cadr x) (cadr y))) <))

と定義し,

(prod a b) => (1 2 3 4 5 6 7 8) = e + f
(prod a c) => (1 1 2 4 4 6 7 8) = 2a + b + d
(prod a d) => (2 3 5 6 6 7 7 8) = b + c + 2d
(prod b c) => (1 3 3 4 5 5 6 7) = a + 2c + d
(prod b d) => (1 2 2 3 4 5 8 8) = a + 2b + c
(prod c d) => (1 2 3 4 5 6 7 8) = e + f

「故に」
2ac+2ad+2bc+2bd= (上の真ん中の4行を足すから) 4a+4b+4c+4d=4e+4f=-2.

左辺は2(a+b)(c+d)=2efなので, ef=-1. e+f=-1/2だったから, 入試問題みたいだが,
x²+1/2*x-1=0
を解いて,
x=-1/4+√(17/16), x=-1/4-√(17/16),

高木先生は前のがeなのは数値的に分かるといわれるので, やってみる.

(apply + (map (lambda (n) (cos (* n (/ (* 2 pi) 17))))
  '(1 2 4 8)))
=> .780776406404415

一方

(- (sqrt (/ 17 16)) (/ 1 4)) => .7807764064044151

eとfが分かったが, まだφが4つも入っているので, aやbを知らなければならない. 幸い, aとbの和(= e)と積(= -1/4)も分かったので, 先ほどと同様に解ける. 後は数値計算だから, WolframAlpha様にお出まし願う. 入試の答をインターネットに聞くのは止めた方がよさそうだが, いまは試験ではないので許されよう.

solve x^2-(-1/4+sqrt(17/16))*x-1/4=0
と入力すると,
x=1/8{-1+√17±&radic(16+(1-√17)²)}
と出た. 高木先生のとすこし違って見えるが, 16+(1-√17)²が34-2√17なので安心する. つまり,

a=1/8{-1+√17+&radic(34-2√17)}
b=1/8{-1+√17-&radic(34-2√17)}

cとdも同じように得られる.

c=1/8{-1-√17+&radic(34-2√17)}
d=1/8{-1-√17-&radic(34-2√17)}

ところで, 前のSchemeで (foo 1 4) => (5 3) だから, cos φ*cos 4φ=(cos 5φ+cos 3φ)/2=c/2. cos φ+cos 4φ=a と一緒にすると, cos φとcos 4φが解ける. そうしてやっと念願の



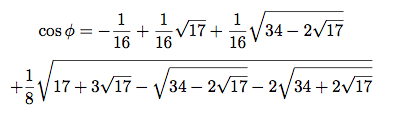
が得られるのであった. それにしても, 最初のa, b, c, dの組分けあたりに気づくところは凄い.