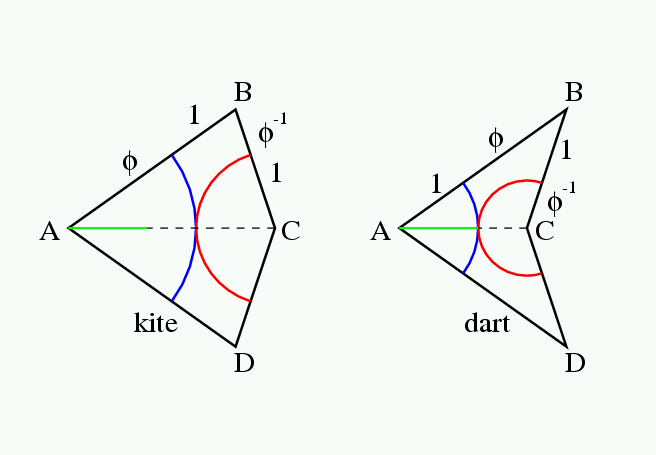
のようにkite(凧)とdart(矢)の2種類のタイルを使うものと,
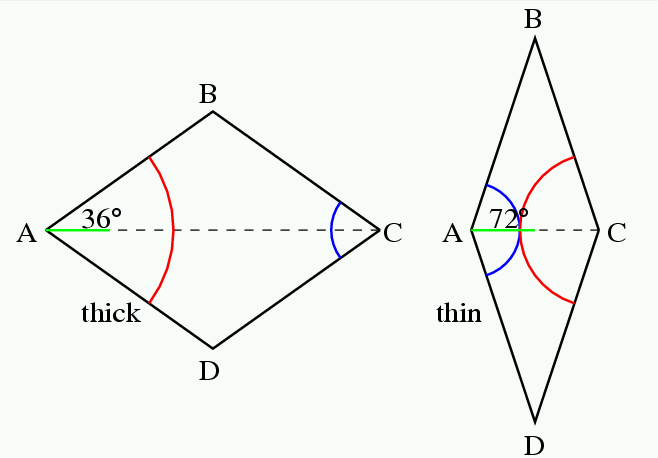
のようにthick(でぶ)とthis(やせ)の2種類のタイルを使うものとがあるらしい.
これらのタイルは, 菱形以外に組合わせると, 平行移動方向の周期的パターンで平面を埋めることが出来ないことで知られている. どちらのタイルにも, 赤と青の円弧が描いてあるのは, 菱形が出来るのを禁止するからで, タイルを置く時は, 同じ色の円弧が接続する必要がある.
従って, 沢山のタイルによるパターンを描くには, タイルを同型のタイルに分割し(これをdeflationという), 再帰的に埋めていく方法を用いる.
分割はタイルの半分について行うので, 分割を示す破線が描いてあり, 緑の線は半分のタイルの起点を示す.
半分のタイルは, 上には0, 下には1をつけて区別する.
今回は, 私がPostScriptで書いたプログラムの話をしたい.
上の2組のタイルの絵は, googleで探したもので, 凧の方はWolfram MathWorldのだ. kiteとdartが長さで与えられ, thickとthinが角度で与えられているのも, 出所が違うからだ.
kiteの辺ABがφ+1, BCがφ-1+1と示されているが, WolframMathWorldにそう書いてあったからだが, kiteの青の円弧の半径がφで, 赤の円弧の半径が1, dartの青の円弧の半径が1で, 赤の円弧の半径がφ-1であることも示す. φはもちろん黄金比 (√5+1)/2である. φの計算に慣れている人には分かるように, φ+1は実はφ2, φ-1+1は実はφである. 従ってAB:BCはφ:1である. kiteとdartは, dartを左右逆にするとkiteに密着出来て菱形になる. 菱形の長い対角線をφ:1に分けた点がCになる. つまりkiteのAC:dartのAC=φ:1. kiteのCABもdartのBCAも2等辺三角形である.
kiteの∠CABを計算しよう. AからBCの中点Eに垂線を引くと, 直角三角形AEBについて, sin ∠EAB=1/2φ=sin 18°, つまり∠CAB=36°である. ゆえに∠ABC = ∠ACB=72°である. dartについては, ∠CAB=∠ABC=36° である.
(注: sin 3α=3 sin α-4 sin3α, cos 2&alpha=1-2 sin2α. &alpha=18°の時, sin 54°=cos 36°からsin 18°は解ける. sin 18°は(√5+1)/4.)
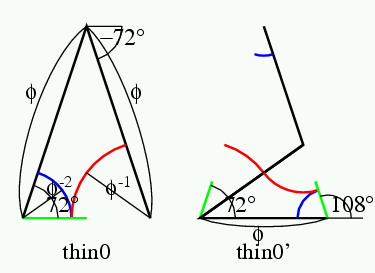
ここでthinの上半分を見ると, ∠CAB=∠ABC=72°だから, thin0はkite0と同じ形である. また大きさは違うが, thick0はdart0と相似形である.
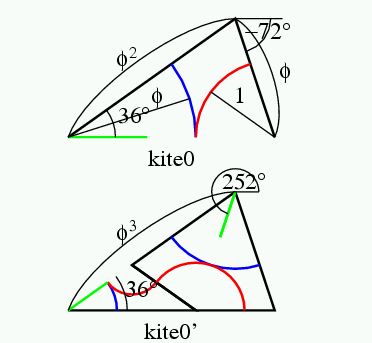
kite0は下のようである. この図の上は, 1個のkite0の描き方で, 左端の原点(緑の線が出発する位置)から, 36°方向へφ2だけ線を引き, 次にそこから-72°方へφだけ引くことを示す.
図の下は, 1個のkite0の分割法で, kite0'が出来るところである. (分割後のタイルにはプライム(')をつけて区別する.)kite0'の左の三角は, dartの片割れだが, 緑の線からdart1であることが分かる. また右の方はkite0とkite1で出来ている. つまり左端に原点を持ち, 36°に向けたdart1を置き, 36°方向へφ2行った所に原点を持ち, 252°に向けたkite0とkite1を置けばよいことを示す. kite0は長い辺がφ, 短い辺が1であった. 分割の結果は, 短い辺がkiteの長い辺で出来ているから, タイルの大きさは1/φになった. 従って, 分割の図のスケールはφ倍で示してある. 上の図のφ2が下の図ではφ3になるのは, そのためである.
そろそろプログラムの出番だ.
描画の出発点は緑の線のついている頂点で, 頂点の座標x, yと緑の基本の線の方向aを貰い, タイルを描く. kite0は(0,0)から出発, 36度の方向にφの長さの線を引く. 次に-72度の方向に1の長さの線を引く. これをPostScriptで
0 0 moveto φ 36 xy lineto one -72 xy rlineto
のように書く. xyは線の長さ l と方向 a を貰い, その先のx, yの位置を返す関数である.
/xy {2 dict begin /a exch def /l exch def l a cos mul l a sin
mul end} def
kite0'の描き方は, まずスケールを1/φにする. (0,0)の位置に36度の方向でdart1を描く. 次は36度の方向にφ行った所を原点とし, -108度の方向でkite0とkite1を描く. 注意点は, φ行ったところといっても, スケールが1/φになっているから, φ2行く必要があることだ. このことさえ忘れなければ, すべての絵は描ける.
0 0 36 dirt1 phi3 36 xy 252 kite0 phi3 36 xy 252 kite1
phi3はφ3に相当する長さのつもりである.
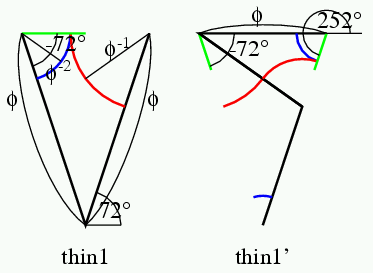
kite1, dart0, dart1の分割は以下の通り.
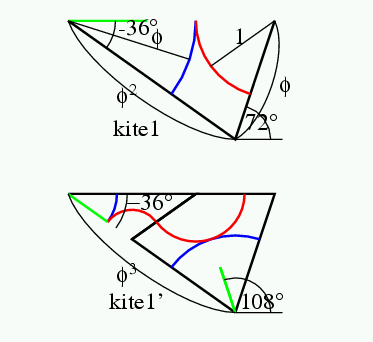
dart0
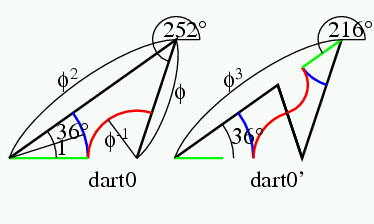
dart1
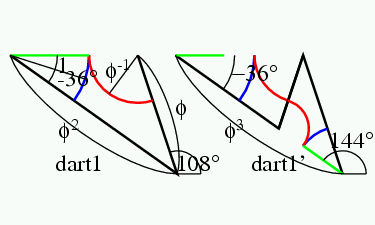
thickとthinも同じだ.
thick0
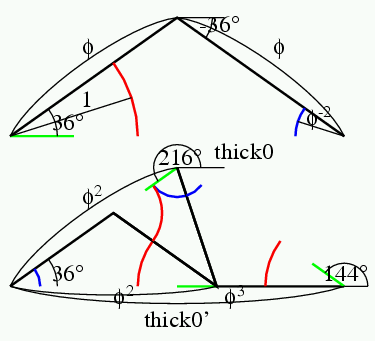
thick1
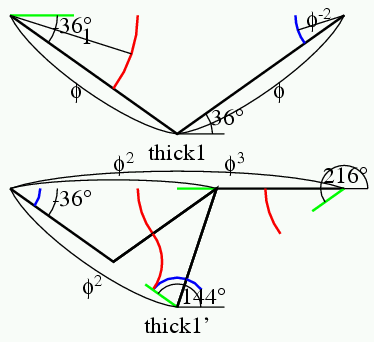
thin0
thin1
kiteとdartのプログラムは以下のとおり.
/phi 5 sqrt 1 add 2 div def /one 80 def
/init {/phs n 5 add array def /f one def
n -1 0 {/i exch def /f f phi div def phs i f put} for
phs n 1 add one put /one one phi mul def phs n 2 add one put
/one one phi mul def phs n 3 add one put
/one one phi mul def phs n 4 add one put} def
/ph {phs exch n add get} def
/xy {2 copy cos mul 3 1 roll sin mul} def
/red {1 0 0 setrgbcolor arc stroke} def
/blue {0 0 1 setrgbcolor arc stroke} def
/green {0 1 0 setrgbcolor 0 0 moveto 1 ph 0 lineto stroke}def
/kite0 {3 dict begin /a exch def /y exch def /x exch def
gsave x y translate a rotate
n 0 eq {0 setgray 0 0 moveto 3 ph 36 xy rlineto
2 ph -72 xy rlineto stroke
0 0 2 ph 0 36 blue 3 ph 0 1 ph 108 180 red green}
{/n n 1 sub def 0 0 36 dart1 4 ph 36 xy 252 kite0
4 ph 36 xy 252 kite1 /n n 1 add def} ifelse
grestore end} def
/kite1 {3 dict begin /a exch def /y exch def /x exch def
gsave x y translate a rotate
n 0 eq {0 setgray 0 0 moveto 3 ph -36 xy rlineto
2 ph 72 xy rlineto stroke
0 0 2 ph -36 0 blue 3 ph 0 1 ph 180 252 red green}
{/n n 1 sub def 0 0 -36 dart0 4 ph -36 xy 108 kite0
4 ph -36 xy 108 kite1 /n n 1 add def} ifelse
grestore end} def
/dart0 {3 dict begin /a exch def /y exch def /x exch def
gsave x y translate a rotate
n 0 eq {0 setgray 0 0 moveto 3 ph 36 xy rlineto
2 ph 252 xy rlineto stroke
0 0 1 ph 0 36 blue 2 ph 0 0 ph 72 180 red green}
{/n n 1 sub def 0 0 0 kite0 4 ph 36 xy 216 dart0
/n n 1 add def} ifelse
grestore end} def
/dart1 {3 dict begin /a exch def /y exch def /x exch def
gsave x y translate a rotate
n 0 eq {0 setgray 0 0 moveto 3 ph -36 xy rlineto
2 ph 108 xy rlineto stroke
0 0 1 ph -36 0 blue 2 ph 0 0 ph 180 288 red green}
{/n n 1 sub def 0 0 0 kite1 4 ph -36 xy 144 dart1
/n n 1 add def} ifelse
grestore end} def
300 400 translate
/n 3 def init
0 72 288 {/a exch def 0 0 a kite0 0 0 a kite1} for
showpage
これで描いたn=3の図は次のようだ.
ここで, 最初に作る配列 phs は, φの等比級数を保持する. 再帰が深くなる, つまり, nが小さくなるにつれ, phsの添字の小さい方を使うようになっている.
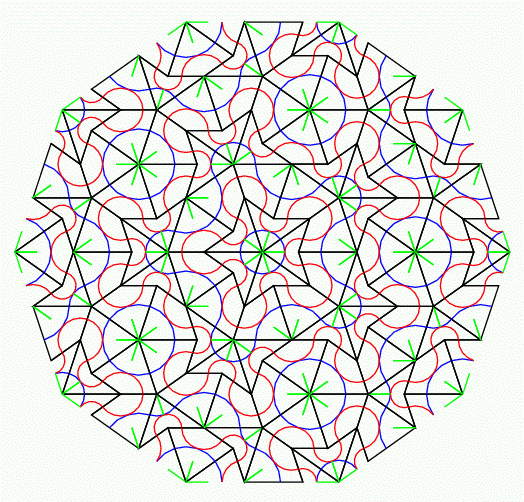
thickとthinも同様なので, 省略する.
余計なことながら, YouTubeにdeflationの面白い動画があった.

1 件のコメント:
8月にPenrose タイルについて質問したものです.並進対称性がなくても回転を使えば描画できるのですね.nを変えながら手元で遊ばさせてもらいました.ありがとうございました.
コメントを投稿