連分数と近似分数

 
 
Martin GardnerがそのThe Unexpected Hanging(ネットで見つかる)の40ページで, 自然対数の底eを近似する, 分母分子とも3桁以内の分数は何かと問うている. その答は覚えやすい878/323 (=2.718266253869969...)だが, その計算法が今回の話題である.

Gardnerは自分では説明せず,
George Chrystal, Algebra An Elementary Text-Book for the Higher Classes of Secondary Schools and for Colleges, Part II. 1906
を見よとしか書いていない. この古典は有名らしく, ネットで探すと読むことができる. (648ページもある!)
http://www.archive.org/details/algebraelementar02chryuoft.pdf

しかしこれは, 高木貞治先生の「初等整数論講義」(手元のは第2版だが)の「中間近似分数」の章にそのものずばりの解説がある.

円周率πの同様な近似値355/113は遥かに有名であった. この分数を得るには連分数を使う.

普通の連分数は



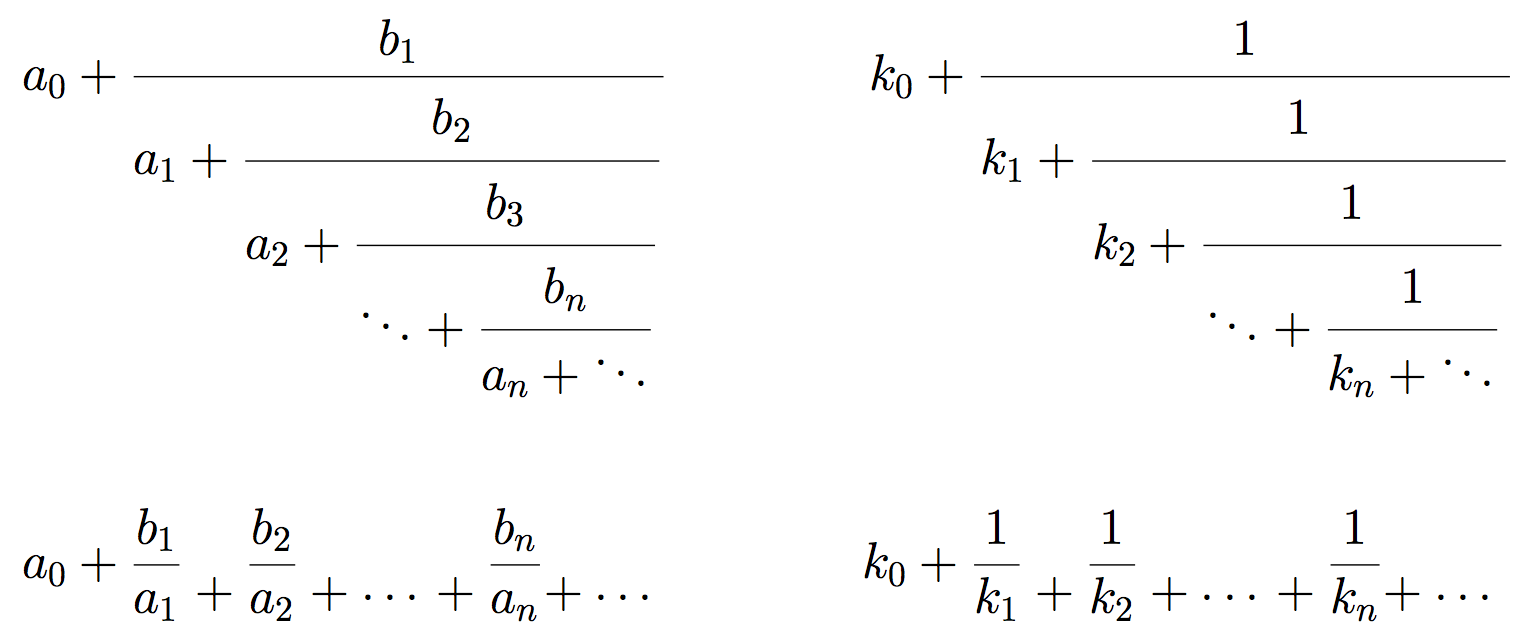
の左上のような形である. この元のTexプログラムは

   \[a_0+{b_1\over\displaystyle a_1+
     {\strut b_2\over\displaystyle a_2+
       {\strut b_3\over\displaystyle\ddots+
         {\strut b_n\over a_n+\ddots
   }}}}\]
   \[a_0+\frac{b_1}{a_1}\:\raisebox{-1.3ex}{+}\:\frac{b_2}{a_2}
      \:\raisebox{-1.3ex}{+}\:\raisebox{-1.ex}{\ldots}\,
   \raisebox{-1.3ex}{+}\:\frac{b_n}{a_n}
   \raisebox{-1.3ex}{+}\:\raisebox{-1.ex}{\ldots}\]

この式にあるb_iを1, a_iを正の整数k_iにしたものを単純(simple)連分数とか正則(regular)連分数といい, 右上のように書き, 物の本にはこれだけを扱ううものが少くない.

こういう表示法は空間をとるので, 通常は下の左や右のように書く. k_iを部分商という.

こういう連分数から, 878/323や355/113のような近似分数が得られる.

円周率πの連分数展開で得られる部分商は7, 15, 1, 292, 1,...
で, この値を順に求める方法が「初等整数論講義」に載っている. これを見ると連分数は, Euclidの互除法に似ていることが分る.



部分商kの値から,


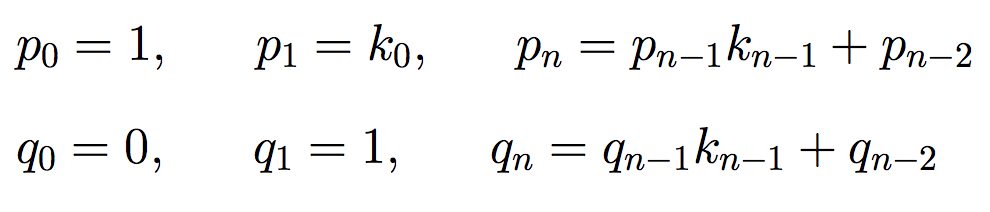
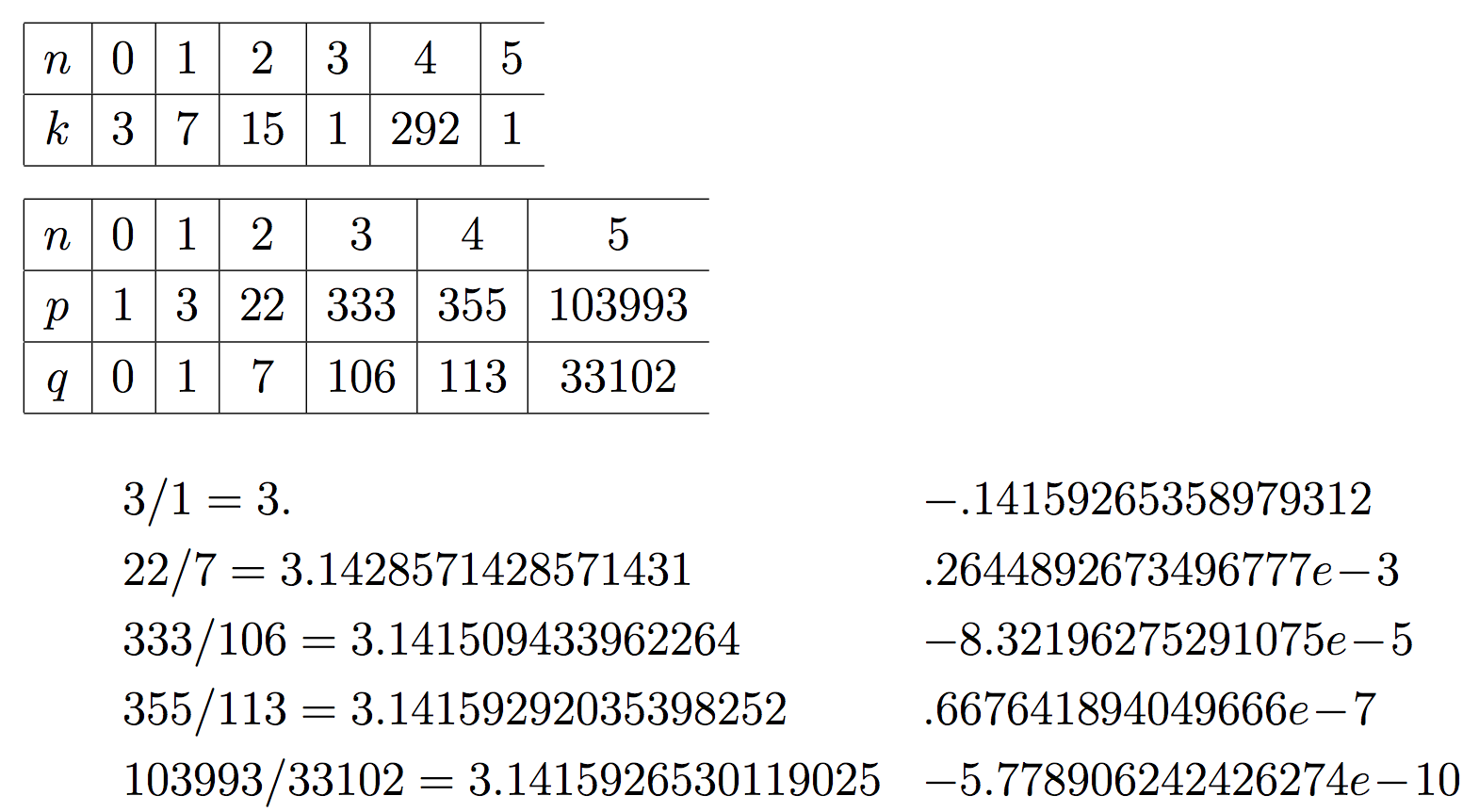
の関係でp, qが計算できる. πの場合のk, p, qは下の表の通り. p/qは連分数の展開を途中で止めたときの分数の値であり, 下の計算のようになる. 各行の右は, 左の分数の値とπとの差で, 見て分るように, 正負が交互に現れる.

この表の下の方に, 355/113がある. この近似分数はこうして発見された.


eについては, 今回はPythonで書いて

import math
x=math.e
ai=[]
while len(ai)<12:
    a=math.floor(x)
    ai.append(a)
    x=1/(x-a)
print(ai)

すると得られた結果は

[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8]


πと同じような表を作ると



しかしこの計算には, 問題の878/323がない. そこで「中間近似分数」が登場する.

 p₅=106, p₆=193,p₇=1264
q₅=39, q₆=71,q₇=465
の間には
p₇-p₅=p₆×k₆
q₇-q₅=q₆×k₆

の関係があるから, pの方は106に193を6回足すと1264になり, qは39に71を6回足すと465になる. この足し算の途中の値r_λ, s_λを分子, 分母にして計算すると, p₅/q₅からp₇/q₇の間の近似値が次々と得られる. これを中間近似分数(intermediate convergents)という.

この計算が次の表である.
    
    
    
そしてこの中に, 問題の878/323があったということだ.