しかし, 情報処理学会コンピュータ博物館のウェブページで, 「PC-1 パラメトロン式計算機」を見ると, 「現在PC-1の現物は存在しないが, 和田英一によりノートPC上でPC-1シミュレータが実現され, 当時のプログラムが動作している.」と書いてあるので, 早く公開しなければと少しずつ公開用の実装を進めていた.
今回, やっとProcessingで実装した同様のシミュレータが完成したので, お目にかけたい. ただ, 私の新しい4CPUのMacBook Airでは順調に走るのだが, 古い方のMacBookAirでは, インディケータが高速には点滅せず, 臨場感がいまいちだ. また私のウェブページパラメトロン計算機 PC-1も参考にされたい.
さて, 今回のシミュレータである.
http://playground.iijlab.net/~ew/pc1sim/pc1sim.html
にアクセスすると, 下のような画面が現れる. これがシミュレータのインターフェースだ.
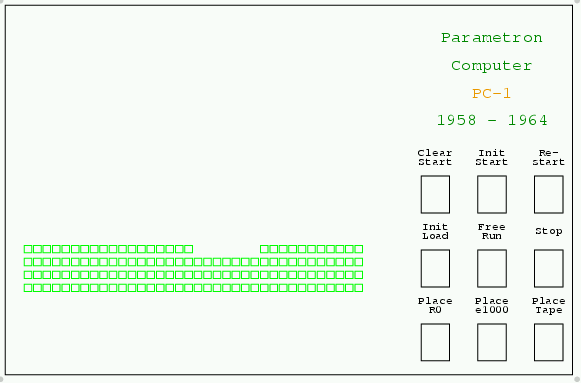
中央左よりの緑の小箱の列は, インディケータで, 最上段の左18ビットが命令レジスタ, その右11ビットがSCC(シーケンスコントロールカウンタ), その下で36個並ぶのは, 上からメモリーレジスタ, アキュムレータ, Rレジスタである. PC-1は1語が18ビットだが, 2語つなげて36ビットを長語として演算が出来た.
各レジスタの内容の0(白で)と1(オレンジ色で)が表示される.
情報処理学会のコンピュータ博物館にパラメトロン計算機PC-1のウェブページがあり, 後藤さんと高橋先生がPC-1の前にいる写真がある. そのPC-1の上の方にネオン管が並んでいるが, それがこのインディケータである.
インディケータの右で3行3列に並ぶ枠がスイッチである. 上の3個は左からクリアスタート(Clear Start), イニシアルスタート(Init Start), リスタート(Restart). リスタートは中断したプログラムを再開する. PC-1では, 停止したとき, 次の命令が命令レジスタに読み出されているから, それを棄て, SCCの示す場所の命令からスタートするのがイニシアルスタートである. さらにSCCを0にした上でイニシアルスタートするのがクリアスタートである.
このシミュレータは先読みしないので, 中と右のスタートは同じである.
中段の3個は左からイニシアルロード(Init Load), フリーラン(Free Run), ストップ(Stop)で, フリーランは連続実行モードをオンにし, ストップはオフにする. オフの時のスタートスイッチは, 命令のステップ実行になる. 左端のイニシアルロードは, イニシアルオーダーのテープを読込む.
下段は左からイニシアルオーダーテープを用意する(Place R0); e1000桁のテープを用意する(Place e1000)スイッチである. 右端は, 他のデモテープを選択する(Place Tape)スイッチで, 現れたメニューから選ぶ.
テープ選択スイッチを押すと,
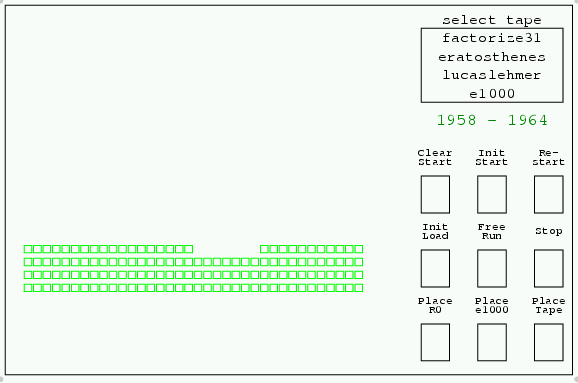
のように右上にメニューが出るので, 使いたいデモプログラムをクリックする.
デモテープは次の4つが用意してある.
a. factorize32 2^31-1, 2^31-3, ..., 2^31-19 を素因数分解する (5分55秒)
b. eratosthenes 篩を使い256から11327までの素数の表を作る (7分)
c. lucaslehmer 3から199までの素数pについてMpの素数性を調べる
d. e1000 自然対数の底eの値を1000桁計算する (6分15秒)
lucas lehmer以外のそれぞれの最後は私が最近ウェブでテストしたの終了までの時間である.
シミュレータを使うには, まず左下のLoad R0スイッチで, イニシアルオーダーR0 のテープを用意する. 次にその上のInit Loadスイッチで, R0を読込む. テープの6列分がメモリーレジスタに読込まれ, 長語(36ビット)として, SCCの表示する0番地, 2番地, ..., に読込まれ, 同時にアキュムレータの各ビットとXORをとってアキュムレータに戻す. 読み終わったとき, アキュムレータが0になるようにパリティビットがテープに入っている.
e1000桁は当時ポピュラーだったデモプログラムである. フリーランにして, クリアスタートでテープ読込みと計算が始まる.
このプログラムは460の階乗分の1までで計算するが, 4回分を一度にまとめて計算するので, インディケータの規則的な繰り返しが115回で計算は終了. その後は結果の二進十進変換になる. このプログラムはR0を壊さないから, 次のデモはR0の再読込みなしで始められる.
factorize31は 231-1, 231-3, 231-5,...231-19を素因数分解するデモプログラムである. このテープは入力サブルーチンのテープを読込んだ後, 停止するから, フリーランをクリックし, リスタートしなければならない. 結果は以下のようになる.
2147483647.=2147483647. 2147483645.=5.19.22605091. 2147483643.=3.715827881. 2147483641.=2699.795659. 2147483639.=7.17.18046081. 2147483637.=3.3.3..13.6118187 2147483635.=5.11.337.115861. 2147483633.=5843.367531. 2147483631.=3.137.263.19867. 2147483629.=2147483629.
最初と最後が素数であり, 特に最初はMersenne素数である. 231の平方根 46340までの疑似素数で割ってみる. 割る値がRレジスタに見えている. 46340は八進法では132404なので, Rレジスタの中央より右が132000くらいになると素数でも計算は終了する.
このデモプログラムはR0を破壊するので, 次のデモの前にはR0を再読込みする必要がある.
eratosthenesの篩 256から11327までの素数を篩で探す. 篩には36ビット長語の32ビットを使い, 残りの4ビットには疑似素数の差を保持する.
最初3で篩い, 次に5で篩い, ..., 11327の平方根106で篩うまで篩えばよいのだが, このプログラムは, 疑似素数の差の循環時に終了テストをするから, 231(八進で347)になるまで篩う. 篩う数はRレジスタに見え, 篩う数が大きくなると, 篩うのに要する時間短くなるのが分かる.
篩終わると, 出力ルーチンが読込まれ, 結果の1315個の素数を持つ素数表257. 263. ... . 11321. が印字される. このデモプログラムはR0を破壊しない.
Lucas Lehmerテスト ある素数pについて, Mp=2p-1が素数の時, MpをMersenne素数という. この素数性を調べるLucas Lehmerテストというのがある. s0=0, sn=sn-12-2(mod Mp)を計算し, sp-2=0(mod Mp)ならMpは素数である.
デモプログラムlucas lehmerはp=2,3,...,199の素数について, Mpの素数性をしらべ, 素数ならpを, 合成数ならcを印字する.
最後まで実行すると相当時間がかかるので, 適当なところで中断しよう. PC-1が活動していた頃, 分かっていたMersenne素数はM3217くらいまでであった.
デモプログラムはplayground.iijlab.net/~ew/pc1sim/{e1000, factorize31, eratosthenes, llt}で見られる.
これらのシミュレーションは50年前の実機より格段に速い. しかしネオン管の明滅は当時を彷彿とさせる. 最近のCPUはブラックボックスになって, なにがどうなっているか分からないが, 当時はこのようなインディケータを眺めて計算の進行状況を知り, 一喜一憂していたものだ. 出力も印刷電信機で, 大きな音をたて, 机をゆさゆさ揺らしながら, 文字を出力していた. あれから半世紀が過ぎた.

1 件のコメント:
はじめまして。
pc-1のシミュレータへのリンクが
たどれません。
学会会員用のページでしょうか?
差し支えがなければ、
一般からも辿り着けるページでも公開をお願いいたしますm(__)m
コメントを投稿