再帰曲線

3次元のHilbert曲線. 前回で2次までは描けることが分かった. まぁしかし, 3次を描くとどうなりそうかにも興味があってやってみた. ご用とお急ぎの方のために, 先ず結果をお目にかけるとこのようになる.



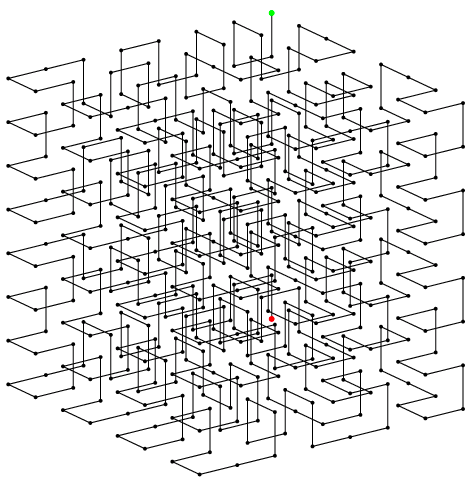
中央少し下の赤い点が出発点, 一番上の緑の点が到着点である. 今回はこの絵の描き方を説明したい.

天下り的だが,

(define (z+y^ d x y z)
 (x+z^ (/ d 2) x y z) (y+z^ (/ d 2) (+ x d) y z)
 (y+z^ (/ d 2) (+ x d) (+ y d) z)
 (z+xv (/ d 2) x (+ y d) z) (z+xv (/ d 2) x (+ y d) (+ z d))
 (y-zv (/ d 2) (+ x d) (+ y d) (+ z d))
 (y-zv (/ d 2) (+ x d) y (+ z d)) (x-zv (/ d 2) x y (+ z d)))

は1辺の長さdのz+y^をx,y,zを起点にして描く起動関数である. 描くといっても, 下請け関数が節点の座標を出力するだけで, 実際に描くのはPostScriptにまかせる.

この関数は下請けを8回呼ぶ. 最初のx+z^の場合は, 下請けの起点は貰ってきたx,y,zである. 次のy+z^の場合は, xを(+ x d), つまりxの位置をdだけずらす. z+y^のGrayコードが000, 001, 011,...と始まったのを反映している. だからその次はyも(+ y d)として呼ぶ. このようにして8回呼ぶと終わる.

その下請けは, やはりそれぞれのGaryコードに基づき,

(define (x+z^ d x y z)
 (p x y z) (p x (+ y d) z) (p x (+ y d) (+ z d)) 
 (p x y (+ z d)) (p (+ x d) y (+ z d))
 (p (+ x d) (+ y d) (+ z d)) (p (+ x d) (+ y d) z)
 (p (+ x d) y z))

(define (y+z^ d x y z)
 (p x y z) (p (+ x d) y z) (p (+ x d) y (+ z d))
 (p x y (+ z d)) (p x (+ y d) (+ z d))
 (p (+ x d) (+ y d) (+ z d))
 (p (+ x d) (+ y d) z) (p x (+ y d) z))
...

のようにして, x+z^, y+z^, z+xv, y-zv, x-zvの5個用意する. (p x y z)は(display (list x y z))である. 座標の8個出力後の改行もpの担当である. (z+y^ 2 0 0 0)と起動関数を呼ぶと, 64個の座標

(0 0 0)(0 1 0)(0 1 1)(0 0 1)(1 0 1)(1 1 1)(1 1 0)(1 0 0)
(2 0 0)(3 0 0)(3 0 1)(2 0 1)(2 1 1)(3 1 1)(3 1 0)(2 1 0)
(2 2 0)(3 2 0)(3 2 1)(2 2 1)(2 3 1)(3 3 1)(3 3 0)(2 3 0)
(1 3 0)(1 2 0)(0 2 0)(0 3 0)(0 3 1)(0 2 1)(1 2 1)(1 3 1)
(1 3 2)(1 2 2)(0 2 2)(0 3 2)(0 3 3)(0 2 3)(1 2 3)(1 3 3)
(2 3 3)(3 3 3)(3 3 2)(2 3 2)(2 2 2)(3 2 2)(3 2 3)(2 2 3)
(2 1 3)(3 1 3)(3 1 2)(2 1 2)(2 0 2)(3 0 2)(3 0 3)(2 0 3)
(1 0 3)(1 1 3)(1 1 2)(1 0 2)(0 0 2)(0 1 2)(0 1 3)(0 0 3)

が得られ, この座標に適当な倍率を掛けて, PostScriptで描くと


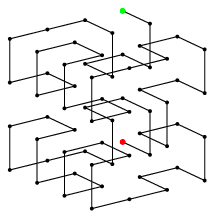
この絵は2次だが, さて, 3次まで描くには, 上にあった起動の関数と下請け関数を統合し,

x+y^ x+yv x+z^ x+zv x-y^ x-yv x-z^ x-zv
y+z^ y+zv y+x^ y+xv y-z^ y-zv y-x^ y-xv
z+x^ z+xv z+y^ z+yv z-x^ z-xv z-y^ z-yv

の24個について関数を書く必要がある. もちろん1個ずつ手書きするわけにはいかない. 当然関数発生関数を書くことになる. それを使い,

(3dgen 2 0 1 0) =>
(define (z+y^ d x y z) (if (= d 1) (begin (p x y z)
(p (+ x d) y z) (p (+ x d) (+ y d) z) (p x (+ y d) z)
(p x (+ y d) (+ z d)) (p (+ x d) (+ y d) (+ z d))
(p (+ x d) y (+ z d)) (p x y (+ z d)))
(begin (x+z^ (/ d 2) x y z) (y+z^ (/ d 2) (+ x d) y z)
(y+z^ (/ d 2) (+ x d) (+ y d) z) (z+xv (/ d 2) x (+ y d) z)
(z+xv (/ d 2) x (+ y d) (+ z d))
(y-zv (/ d 2) (+ x d) (+ y d) (+ z d))
(y-zv (/ d 2) (+ x d) y (+ z d)) (x-zv (/ d 2) x y (+ z d)))))

のような関数を24個揃える. そして(z+y^ 4 0 0 0)と起動すると, 512個の座標

(0 0 0)(0 0 1)(1 0 1)(1 0 0)(1 1 0)(1 1 1)(0 1 1)(0 1 0)
(0 2 0)(0 3 0)(1 3 0)(1 2 0)(1 2 1)(1 3 1)(0 3 1)(0 2 1)
(0 2 2)(0 3 2)(1 3 2)(1 2 2)(1 2 3)(1 3 3)(0 3 3)(0 2 3)
(0 1 3)(0 1 2)(0 0 2)(0 0 3)(1 0 3)(1 0 2)(1 1 2)(1 1 3)
(2 1 3)(2 1 2)(2 0 2)(2 0 3)(3 0 3)(3 0 2)(3 1 2)(3 1 3)
(3 2 3)(3 3 3)(2 3 3)(2 2 3)(2 2 2)(2 3 2)(3 3 2)(3 2 2)
(3 2 1)(3 3 1)(2 3 1)(2 2 1)(2 2 0)(2 3 0)(3 3 0)(3 2 0)
(3 1 0)(3 1 1)(2 1 1)(2 1 0)(2 0 0)(2 0 1)(3 0 1)(3 0 0)

(4 0 0)(4 0 1)(4 1 1)(4 1 0)(5 1 0)(5 1 1)(5 0 1)(5 0 0)
(6 0 0)(7 0 0)(7 1 0)(6 1 0)(6 1 1)(7 1 1)(7 0 1)(6 0 1)
(6 0 2)(7 0 2)(7 1 2)(6 1 2)(6 1 3)(7 1 3)(7 0 3)(6 0 3)
(5 0 3)(5 0 2)(4 0 2)(4 0 3)(4 1 3)(4 1 2)(5 1 2)(5 1 3)
(5 2 3)(5 2 2)(4 2 2)(4 2 3)(4 3 3)(4 3 2)(5 3 2)(5 3 3)
(6 3 3)(7 3 3)(7 2 3)(6 2 3)(6 2 2)(7 2 2)(7 3 2)(6 3 2)
(6 3 1)(7 3 1)(7 2 1)(6 2 1)(6 2 0)(7 2 0)(7 3 0)(6 3 0)
(5 3 0)(5 3 1)(5 2 1)(5 2 0)(4 2 0)(4 2 1)(4 3 1)(4 3 0)

(4 4 0)(4 4 1)(4 5 1)(4 5 0)(5 5 0)(5 5 1)(5 4 1)(5 4 0)
(6 4 0)(7 4 0)(7 5 0)(6 5 0)(6 5 1)(7 5 1)(7 4 1)(6 4 1)
(6 4 2)(7 4 2)(7 5 2)(6 5 2)(6 5 3)(7 5 3)(7 4 3)(6 4 3)
(5 4 3)(5 4 2)(4 4 2)(4 4 3)(4 5 3)(4 5 2)(5 5 2)(5 5 3)
(5 6 3)(5 6 2)(4 6 2)(4 6 3)(4 7 3)(4 7 2)(5 7 2)(5 7 3)
(6 7 3)(7 7 3)(7 6 3)(6 6 3)(6 6 2)(7 6 2)(7 7 2)(6 7 2)
(6 7 1)(7 7 1)(7 6 1)(6 6 1)(6 6 0)(7 6 0)(7 7 0)(6 7 0)
(5 7 0)(5 7 1)(5 6 1)(5 6 0)(4 6 0)(4 6 1)(4 7 1)(4 7 0)

(3 7 0)(2 7 0)(2 7 1)(3 7 1)(3 6 1)(2 6 1)(2 6 0)(3 6 0)
(3 5 0)(3 4 0)(3 4 1)(3 5 1)(2 5 1)(2 4 1)(2 4 0)(2 5 0)
(1 5 0)(1 4 0)(1 4 1)(1 5 1)(0 5 1)(0 4 1)(0 4 0)(0 5 0)
(0 6 0)(1 6 0)(1 7 0)(0 7 0)(0 7 1)(1 7 1)(1 6 1)(0 6 1)
(0 6 2)(1 6 2)(1 7 2)(0 7 2)(0 7 3)(1 7 3)(1 6 3)(0 6 3)
(0 5 3)(0 4 3)(0 4 2)(0 5 2)(1 5 2)(1 4 2)(1 4 3)(1 5 3)
(2 5 3)(2 4 3)(2 4 2)(2 5 2)(3 5 2)(3 4 2)(3 4 3)(3 5 3)
(3 6 3)(2 6 3)(2 6 2)(3 6 2)(3 7 2)(2 7 2)(2 7 3)(3 7 3)

(3 7 4)(2 7 4)(2 7 5)(3 7 5)(3 6 5)(2 6 5)(2 6 4)(3 6 4)
(3 5 4)(3 4 4)(3 4 5)(3 5 5)(2 5 5)(2 4 5)(2 4 4)(2 5 4)
(1 5 4)(1 4 4)(1 4 5)(1 5 5)(0 5 5)(0 4 5)(0 4 4)(0 5 4)
(0 6 4)(1 6 4)(1 7 4)(0 7 4)(0 7 5)(1 7 5)(1 6 5)(0 6 5)
(0 6 6)(1 6 6)(1 7 6)(0 7 6)(0 7 7)(1 7 7)(1 6 7)(0 6 7)
(0 5 7)(0 4 7)(0 4 6)(0 5 6)(1 5 6)(1 4 6)(1 4 7)(1 5 7)
(2 5 7)(2 4 7)(2 4 6)(2 5 6)(3 5 6)(3 4 6)(3 4 7)(3 5 7)
(3 6 7)(2 6 7)(2 6 6)(3 6 6)(3 7 6)(2 7 6)(2 7 7)(3 7 7)

(4 7 7)(4 7 6)(4 6 6)(4 6 7)(5 6 7)(5 6 6)(5 7 6)(5 7 7)
(6 7 7)(7 7 7)(7 6 7)(6 6 7)(6 6 6)(7 6 6)(7 7 6)(6 7 6)
(6 7 5)(7 7 5)(7 6 5)(6 6 5)(6 6 4)(7 6 4)(7 7 4)(6 7 4)
(5 7 4)(5 7 5)(4 7 5)(4 7 4)(4 6 4)(4 6 5)(5 6 5)(5 6 4)
(5 5 4)(5 5 5)(4 5 5)(4 5 4)(4 4 4)(4 4 5)(5 4 5)(5 4 4)
(6 4 4)(7 4 4)(7 5 4)(6 5 4)(6 5 5)(7 5 5)(7 4 5)(6 4 5)
(6 4 6)(7 4 6)(7 5 6)(6 5 6)(6 5 7)(7 5 7)(7 4 7)(6 4 7)
(5 4 7)(5 4 6)(5 5 6)(5 5 7)(4 5 7)(4 5 6)(4 4 6)(4 4 7)

(4 3 7)(4 3 6)(4 2 6)(4 2 7)(5 2 7)(5 2 6)(5 3 6)(5 3 7)
(6 3 7)(7 3 7)(7 2 7)(6 2 7)(6 2 6)(7 2 6)(7 3 6)(6 3 6)
(6 3 5)(7 3 5)(7 2 5)(6 2 5)(6 2 4)(7 2 4)(7 3 4)(6 3 4)
(5 3 4)(5 3 5)(4 3 5)(4 3 4)(4 2 4)(4 2 5)(5 2 5)(5 2 4)
(5 1 4)(5 1 5)(4 1 5)(4 1 4)(4 0 4)(4 0 5)(5 0 5)(5 0 4)
(6 0 4)(7 0 4)(7 1 4)(6 1 4)(6 1 5)(7 1 5)(7 0 5)(6 0 5)
(6 0 6)(7 0 6)(7 1 6)(6 1 6)(6 1 7)(7 1 7)(7 0 7)(6 0 7)
(5 0 7)(5 0 6)(5 1 6)(5 1 7)(4 1 7)(4 1 6)(4 0 6)(4 0 7)

(3 0 7)(3 0 6)(2 0 6)(2 0 7)(2 1 7)(2 1 6)(3 1 6)(3 1 7)
(3 2 7)(3 3 7)(2 3 7)(2 2 7)(2 2 6)(2 3 6)(3 3 6)(3 2 6)
(3 2 5)(3 3 5)(2 3 5)(2 2 5)(2 2 4)(2 3 4)(3 3 4)(3 2 4)
(3 1 4)(3 1 5)(3 0 5)(3 0 4)(2 0 4)(2 0 5)(2 1 5)(2 1 4)
(1 1 4)(1 1 5)(1 0 5)(1 0 4)(0 0 4)(0 0 5)(0 1 5)(0 1 4)
(0 2 4)(0 3 4)(1 3 4)(1 2 4)(1 2 5)(1 3 5)(0 3 5)(0 2 5)
(0 2 6)(0 3 6)(1 3 6)(1 2 6)(1 2 7)(1 3 7)(0 3 7)(0 2 7)
(0 1 7)(0 1 6)(1 1 6)(1 1 7)(1 0 7)(1 0 6)(0 0 6)(0 0 7)

が得られ, 始めの図が描けることになった. 折角描いてはみたが, 期待したほどには美しくなかったのが残念だ.

私がHilbert曲線の話を書いたのは2009年6月19日のブログであった. そこの図で分かるように, 2次元の曲線では, 1次の曲線が縦向きに出発するなら, 2次は横向き, 3次はまた縦向き,...のように交互に出発する.

今回, 3次元のHilbert曲線を3次まで描いて分かったのは, 前回のブログの最初の図で, 赤線の1次の曲線が0からx軸方向へ出発し, 2次が0からy軸方向へ出発したのに対し, 今回の図では, 赤点から予想通りz方向へ出発していることだ. そういうものだったのだ.

上の64行にわたる512の座標は, 8行ずつ8つのブロックにして書いてある. ブロックを上から順に0,1,2,...,7ということにすると, ブロック0の座標はxもyもzも0から3である.つまり原点に近い1/8の空間を占めている. ブロック1はxが4から7なので, x方向だけが4ずれた空間にある. 最後のブロック7はzが4から7で, z方向へずれた空間にあるわけだ.

ブロック0をもう一度書いてみる.

(0 0 0)(0 0 1)(1 0 1)(1 0 0)(1 1 0)(1 1 1)(0 1 1)(0 1 0)
(0 2 0)(0 3 0)(1 3 0)(1 2 0)(1 2 1)(1 3 1)(0 3 1)(0 2 1)
(0 2 2)(0 3 2)(1 3 2)(1 2 2)(1 2 3)(1 3 3)(0 3 3)(0 2 3)
(0 1 3)(0 1 2)(0 0 2)(0 0 3)(1 0 3)(1 0 2)(1 1 2)(1 1 3)
(2 1 3)(2 1 2)(2 0 2)(2 0 3)(3 0 3)(3 0 2)(3 1 2)(3 1 3)
(3 2 3)(3 3 3)(2 3 3)(2 2 3)(2 2 2)(2 3 2)(3 3 2)(3 2 2)
(3 2 1)(3 3 1)(2 3 1)(2 2 1)(2 2 0)(2 3 0)(3 3 0)(3 2 0)
(3 1 0)(3 1 1)(2 1 1)(2 1 0)(2 0 0)(2 0 1)(3 0 1)(3 0 0)

赤く書いてあるのは, すべての座標が2で割り切れるもので, 各行の1つずる現れる. 各行が1つのGrayコードになっていて, その原点に近いものがそれである. 下の図の8つの赤点に対応する.

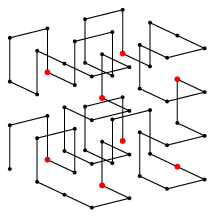
それを2で割ると

(0 0 0)(0 1 0)(0 1 1)(0 0 1)(1 0 1)(1 1 1)(1 1 0)(1 0 0)

となり, 2次の64個の座標の1行目と同じになるが, 当たり前だ.