平方剰余

MathworldのQuadratic Residueを見ると, 10月1日のブログUlam Spiralのような, なんやらフラクタル風の図がある. これもやはり自分でも描くべしと, 調べてみた.

Quadratic Residue, つまり平方剰余に興味を持つ人には時々出会う.

まずaがpの平方剰余であるとは, 0<x<pのxについて, x²=a (mod p)となるxがあることだ. 従って, この範囲のについて計算すると, たとえばp=10として

(define p 10)
(map (lambda (x) (modulo (* x x) p)) (a2b 1 p))
=>(1 4 9 6 5 6 9 4 1)

従って10に対しては, 1,4,5,6,9が平方剰余であり, ここに現れない2,3,7,8が平方非剰余(Quadratic Nonresidue)である. 上の計算で見る通り, 1からp-1のxに対して, 現れる平方剰余は対称なので, 真ん中まで計算すれば良い.

従って

(define (quadratic-residue p)
 (map (lambda (x) (modulo (* x x) p))
  (a2b 1 (+ (quotient p 2) 1))))

(quadratic-residue 10) => (1 4 9 6 5)
(quadratic-residue 11) => (1 4 9 5 3)
(quadratic-residue 12) => (1 4 9 4 1 0)
(quadratic-residue 13) => (1 4 9 3 12 10)

0は平方剰余と言わないらしいから, 0を除き, nubを使って重複を省き, 大きさの順にするには,

(define (quadratic-residue p)
 (sort (nub (filter (lambda (x) (> x 0))
  (map (lambda (x) (modulo (* x x) p))
   (a2b 1 (+ (quotient p 2) 1)))
   )) <))

(map (lambda (p) (quadratic-residue p)) (a2b 10 14))
=> ((1 4 5 6 9) (1 3 4 5 9) (1 4 9) (1 3 4 9 10 12))

これを見るとどれにも1,4,9があるが, xが1,2,3の時のもので当然だ.

そこで, p=2から40までの平方剰余を計算してみると

(for-each (lambda (p) (display p) 
 (display (quadratic-residue p)) (newline))
 (a2b 2 41))
=>
2(1)
3(1)
4(1)
5(1 4)
6(1 3 4)
7(1 2 4)
8(1 4)
9(1 4 7)
10(1 4 5 6 9)
11(1 3 4 5 9)
12(1 4 9)
13(1 3 4 9 10 12)
14(1 2 4 7 8 9 11)
15(1 4 6 9 10)
16(1 4 9)
17(1 2 4 8 9 13 15 16)
18(1 4 7 9 10 13 16)
19(1 4 5 6 7 9 11 16 17)
20(1 4 5 9 16)
21(1 4 7 9 15 16 18)
22(1 3 4 5 9 11 12 14 15 16 20)
23(1 2 3 4 6 8 9 12 13 16 18)
24(1 4 9 12 16)
25(1 4 6 9 11 14 16 19 21 24)
26(1 3 4 9 10 12 13 14 16 17 22 23 25)
27(1 4 7 9 10 13 16 19 22 25)
28(1 4 8 9 16 21 25)
29(1 4 5 6 7 9 13 16 20 22 23 24 25 28)
30(1 4 6 9 10 15 16 19 21 24 25)
31(1 2 4 5 7 8 9 10 14 16 18 19 20 25 28)
32(1 4 9 16 17 25)
33(1 3 4 9 12 15 16 22 25 27 31)
34(1 2 4 8 9 13 15 16 17 18 19 21 25 26 30 32 33)
35(1 4 9 11 14 15 16 21 25 29 30)
36(1 4 9 13 16 25 28)
37(1 3 4 7 9 10 11 12 16 21 25 26 27 28 30 33 34 36)
38(1 4 5 6 7 9 11 16 17 19 20 23 24 25 26 28 30 35 36)
39(1 3 4 9 10 12 13 16 22 25 27 30 36)
40(1 4 9 16 20 24 25 36)

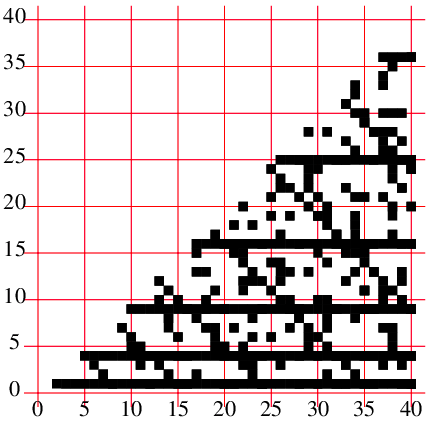
これを使って描いたのが次の図である.


p=200までを描くと


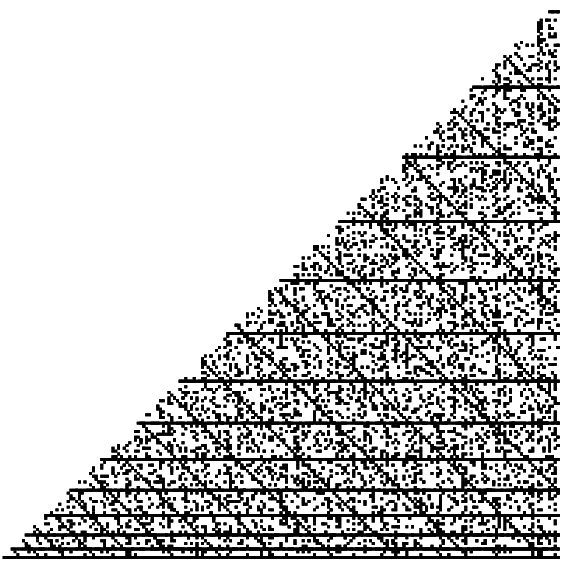
これは, 最初に述べた, Mathworldにあった図と同じである.

PostScriptのプログラムは

40 40 translate
/d 2 def
/dot {2 dict begin /b exch def /a exch def a d mul
b d mul moveto d 0 rlineto 0 d rlineto d neg 0 rlineto
closepath fill end} def

1 1 200{/p exch def
1 1 p 1 sub{/x exch def
/a x x mul p mod def
a 0 gt {p a dot} if} for} for

のようになっている.

高さ1,4,9のような横線の他に, 右下がりの線も目立つ. つまり座標でいうと(5,4)(6,3)(7,2)(8,1)の線; (9,7)(10,6)(11,5)(12,4)(13,3)(14,2)(15,1)の線などだ. 最初の線はxとyの和が9, 次のでは和が16なのに気づく.

最初の(5,4)は, 5を法として, 4は平方剰余であるということだが, 4に法の5を足してみると9になり, 3掛ける3を5で割った余りが4なのである. その次の(6,3)は同じ9は6を法として3であるということで, この線は9を9未満の数で割った剰余の線. 次は16を16未満の数で割った剰余の線であった.