私の愛読書の1つ, E.M.Reingold, N. DershowitzのCalendrical Calculationsでその辺の計算法を見てみよう. ユリウス日は, Julian暦-4712年1月1日が起点だが, 本書のカレンダーの起点は, Gregorian暦を昔の方へ外挿した1年1月1日を1とし, それからのFixed Day Numberで表わす. この日数をR.D.(Rata Die, fixed dateのラテン語)という.
本書の関数は, 本文では不思議な構文で書いてあり, 付録にはCommon Lispによる実装があるが, Scheme風にすると,
(define gregorian-epoch 1)
(define (gregorian-leap? y)
(and (= (modulo y 4) 0)
(not (member (modulo y 400) '(100 200 300)))))
(define (fixed-from-gregorian y m d)
(+ gregorian-epoch -1 (* 365 (- y 1)) (quotient (- y 1) 4)
(- (quotient (- y 1) 100)) (quotient (- y 1) 400)
(quotient (- (* 367 m) 362) 12)
(cond ((<= m 2) 0)
((gregorian-leap? y) -1)
(else -2)) d))
(fixed-from-gregorian 1 1 1) => 1
(fixed-from-gregorian 2011 5 16) => 734273
この本では, 年内の日数と月の変換は, 2月も30日あるとして計算し, 補正する
(map (lambda (m) (quotient (- (* 367 m) 362) 12)) (a2b 1 13))
=> (0 31 61 92 122 153 183 214 245 275 306 336)
floorをとらないと, 以下のような値である.
(.417 31. 61.583 92.167 122.75 153.333 183.917 214.5
245.083 275.667 306.25 336.833)
隣り同士の差を取ってみると,
(map (lambda (a b) (- a b))
'(31 61 92 122 153 183 214 245 275 306 336)
'(0 31 61 92 122 153 183 214 245 275 306))
=>
(31 30 31 30 31 30 31 31 30 31 30)
補正は, 1月2月はこのまま, 3月から後はうるう年なら1を引き, 平年なら2を引く.
さて, Gregorian暦のy, m, dからfixed dateを得る最初の関数fixed-from-gregorianの解説である.
前年までの経過日数が必要なので, (- y 1)が頻出する.
(* 365 (- y 1)) ;前年までの平日の日数
(quotient (- y 1) 4) ;Julian暦のうるう日の日数
(- (quotient (- y 1) -100)) ;100年の倍数の年はうるうをやめる
(quotient (- y 1) 400) ;しかし400年の倍数なら, やはりうる
う年にする
(quotient (- (* 367 m) 362) 12) ;2月を30日と仮定して, m月
の前月までの日数
(cond ((<= m 2) 0) ;補正
((gregorian-leap? y) -1)
(else -2)) d)) ;dを足す.
最初のgregorian-epochは, 1年1月1日を1にするためである.
最後のテスト例のようにうまく行く.
予想通り, 逆は難しい. プログラムは以下のようだ.
(define (gregorian-year-from-fixed rd)
(let* ((d0 (- rd gregorian-epoch))
(n400 (quotient d0 146097))
(d1 (modulo d0 146097))
(n100 (quotient d1 36524))
(d2 (modulo d1 36524))
(n4 (quotient d2 1461))
(d3 (modulo d2 1461))
(n1 (quotient d3 365))
(y (+ (* 400 n400) (* 100 n100) (* 4 n4) n1)))
(if (or (= n100 4) (= n1 4)) y (+ y 1))))
(define (gregorian-from-fixed rd)
(let* ((y (gregorian-year-from-fixed rd))
(prior-days (- rd (fixed-from-gregorian y 1 1))
(correction (cond ((< rd (fixed-from-gregorian y 3 1)) 0)
((gregorian-leap? y) 1
(else 2)))
(m (quotient (+ (* 12 (+ prior-days correction)) 373)
367))
(d (+ (- rd (fixed-from-gregorian y m 1)) 1)))
(list y m d)))
(gregorian-from-fixed 1) => (1 1 1)
(gregorian-from-fixed 734273) => (2011 5 16)
と定義しておき, (gregorian-year-from-fixed rd)
で rd に対する年 y を計算する.
(n400 (quotient d0 146097)) :d0に400年の日数が何回あるか見る. 146097は400年の日数.
(d1 (modulo d0 146097)) :その400年内の日数
(n100 (quotient d1 36524)) ;その日数に100年は何回あるか. しかし400年の100年の日数は, 最初の100年の先頭の00年はうるう年なので, 36525日あるから
(d2 (modulo d1 36524)) ;その100年内の日数
(n4 (quotient d2 1461)) ;その日数内の4年の数
(d3 (modulo d2 1461)) ;その4年内の日数
(n1 (quotient d3 365)) ;4年内の1年の数
(n1 (quotient d3 365)) ;4年内の1年の数
基数変換をやっているみたいに簡単なのに驚く. 400年の中の日数d1のいろいろな値から得られるyをみてみる.
(define (gregorian-year-from-fixed rd)
(let* ((n100 (quotient rd 36524))
(d2 (modulo d 36524))
(n4 (quotient d2 1461))
(d3 (modulo d2 1461))
(n1 (quotient d3 365))
(y (+ (* 100 n100) (* 4 n4) n1)))
(if (or (= n100 4) (= n1 4)) y (+ y 1))))
すると, 以下のようになっていることが分かる.
rd y rd y
0- 364 1 365 35794- 36158 99 365
365- 729 2 365 36159- 36523 100 365
730- 1094 3 365 36524- 36888 101 365
1095- 1460 4 366
1461- 1825 5 365 72318- 72682 199 365
1826- 2190 6 365 72683- 73047 200 365
2191- 2555 7 365 73088- 73412 201 365
2556- 2921 8 366
2922- 3286 9 365 108842-109206 299 365
3287- 3651 10 365 109207-109571 300 365
3652- 4016 11 365 109572-109936 301 365
4017- 4382 12 366
4383 4747 13 365 145001-145365 398 365
4748- 5112 14 365 145366-145730 399 365
5113- 5477 15 365 145731-146096 400 366
5478- 5843 16 366
0から勘定を始めるのが基本と思っている私なら, 下の図の左のような関数を書くところだが, 本書の流儀は違う. d1=0ならy=1が返る. d1=146096なら, y=400であった. なるほど! (図の太い横線は366日の年を示す. 横線の左の黒丸は閉区間, 右の白丸は開区間を示す.)

別の図を描くと下のようになる. つまり, 図で網掛けの例外を最後に置くので計算が簡単になっていたのだ.
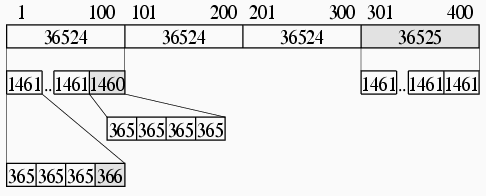
それなら, 私の流儀でも, 400年紀末から逆に計算すればおなじわけだった.
ところで, これではまだfixedから, 年が得られただけである. 本番のプログラムはこれを下請けに使う(gregorian-from-fixed d)である. その解法はこうだ.
とりあえずこのrdの落ちるyを求める. 次のその年の1月1日のfixed dateを求め, prior-daysとする. その年の3月1日のfixed dateを求め, prior-daysがそれより小さければ, 補正は0, そうでなくて, うるう年なら補正は1, 平年なら補正は2である. 次に前に日数を計算した式で, 月を見つけ, その月の1日のfixed dateとの差から, 日が分かるのである.
fixed-dateを何回も使うが, それだけ分かりやすいアルゴリズムになっている.
こういうプログラムの解読もなかなか面白い.

0 件のコメント:
コメントを投稿