再帰曲線

dragon曲線と, twindragonのフラクタルの絵は, 関係がありそうでなさそうである. TAOCPには "B. Mandelbrot named S the "twindragon" because he noticed that it is essentially obtained by joining two "dragon curves" belly-to-belly." と書いてあるが(演習問題4.1-18の解答), その意味は, 前回引用したWilliam Gilbertの論文を見て分かった.

前回のtwindragonの絵は, i-1進法の小数であったが, i-1進法の整数でも話はほとんど同じである.(...a₃a₂a₁a₀)₂は

n = &Sigma_k=0 a_k*(i-1)^k

を表わす.


整数版のtwindragonの絵を描くには, まず原点に...=a₃=a₂=a₁=a₀=0に対する0の点を置く. 次にa₀だけが1で他が0の1の点は1*(i-1)⁰=1 なので, (1,0)に置く.

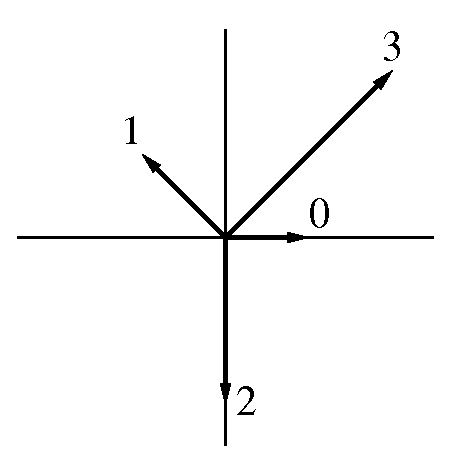
前回にも書いたように, 次の2と3は, 0と1の点を(-1,1)だけ移動するのだが, これは(i-1)¹=i-1だからである. 上の図の1の矢印の向きである.

冪が2になると, これは1の矢印の2乗で, (i-1)²=i²+2i+1=-2iの方向へ, 0,1,2,3の点を移動する.

i-1の冪乗は, いちいち計算することはない. 昔々習った複素数の乗算z₀*z₁=zでは, zの偏角は, z₀の偏角とz₁の偏角の和だし, zの絶対値は, z₀の絶対値とz₁の絶対値の積であった.

だから, 2の矢印は, 1の矢印をもう135度回して下向きにし, 1の矢印の絶対値√2の2乗で2の長さにする. それが矢印2である.

矢印2に矢印1を掛けると, 偏角はまた同じだけまわり, 右上45度を向く. 絶対値は2の√2倍だから, 2掛ける2の正方形の対角線になる. 矢印3の先は, 点(2,2)である.

要するに次々の矢印は, 135度回転し, 長さを√2倍すればよいことが分かる.

√2倍というのは, A版, B版の紙の大きさを連想させる. つまりAn版の紙を2枚横に並べる. その上にAn-1版の紙を並べる. その横にAn-2版の紙を並べる. ... twindragonの絵はこういうものだったかと考えると, 有難みは減る. そういえば規格の紙の寸法は, フラクタルの身近な例であったのだ.



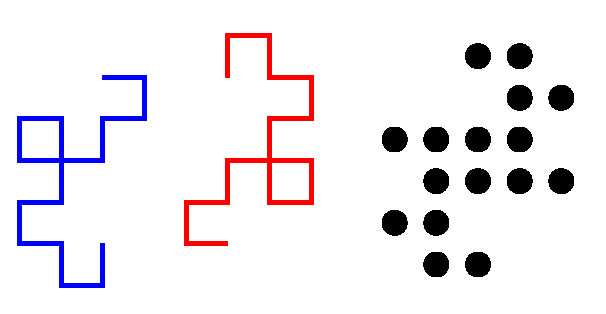
さて, dragon曲線とフラクタル図の関係である. 上の図に, モンゴル出身力士のような, 青竜と赤竜を示す. 点対称になっている. またフラクタル図も示した. 青竜と赤竜の端点はちょうど左右に並ぶように描いてある. これを端点が繋がるようにずらし, さらにフラクタルもずらすと, 竜の縦線とフラクタルの点が一致するのである. 驚きだ!

ついでにいくつかの竜についても描いたのが, 下の図である.



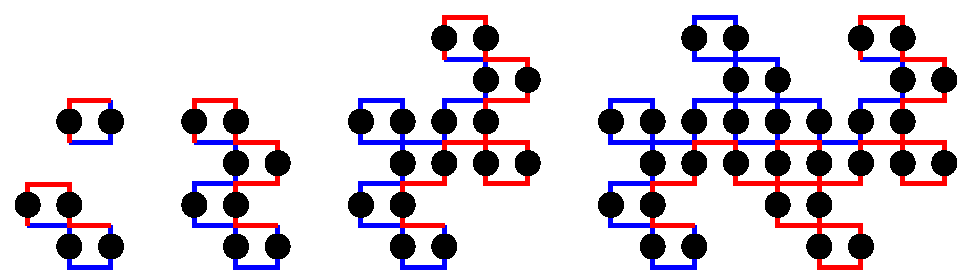
こういうことに気づくとは, さすがMandelbrotである.


1958年秋, IBMのOssiningの研究所に, 先輩の蒲生秀也先生を訪問した時, 先生はMandelbrotがその研究所にいるので, 紹介しようといわれたが, その日Mandelbrotはたまたま休暇で, 会うことは出来なかった.