連分数と近似分数

前回のブログ, 連分数と近似分数でeの近似分数 878/323をStern Brocot木から求めたが, 連分数との関係については書かなかった.

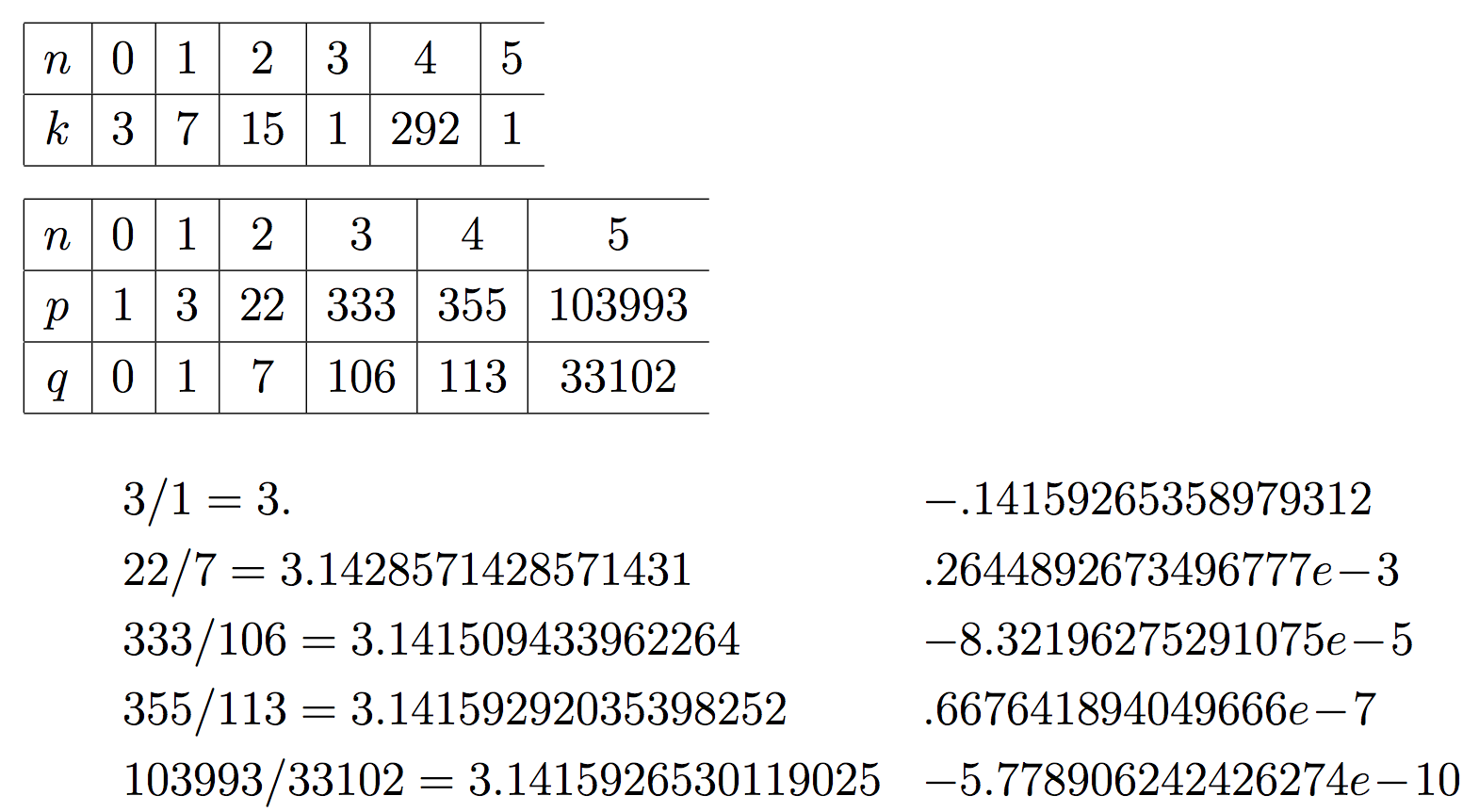
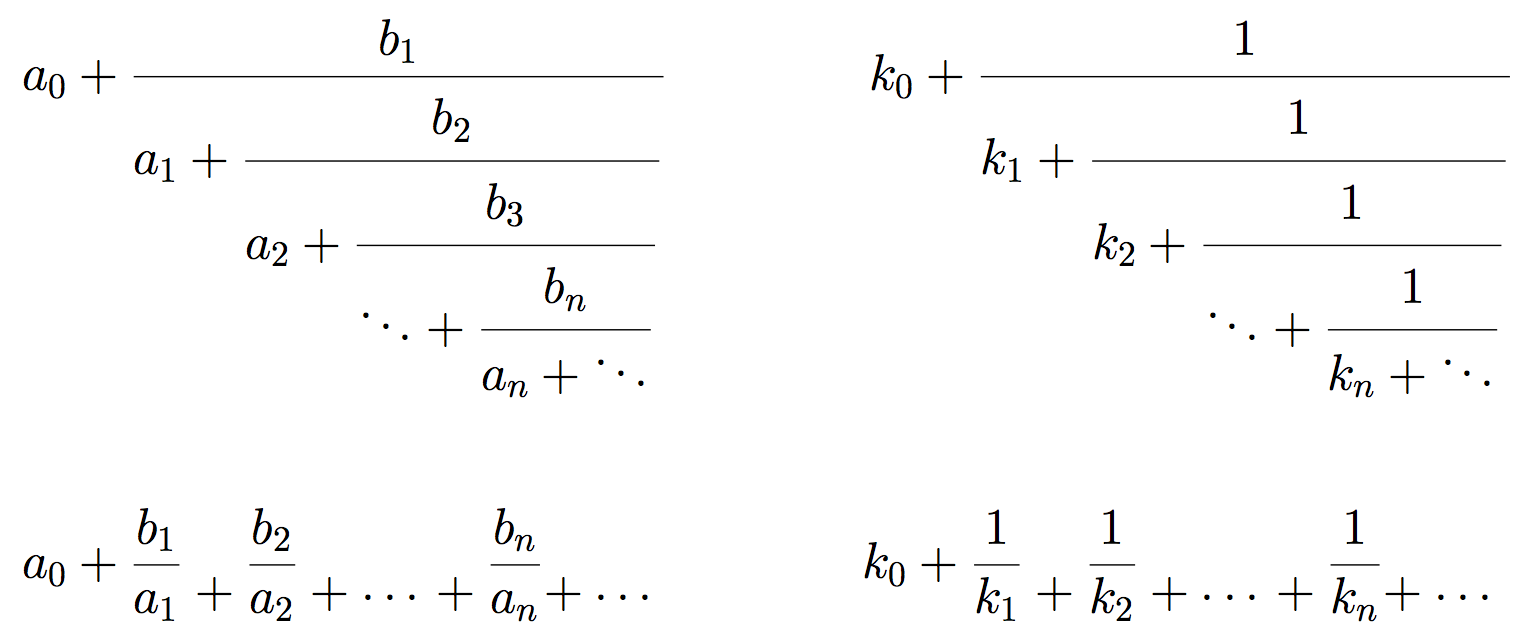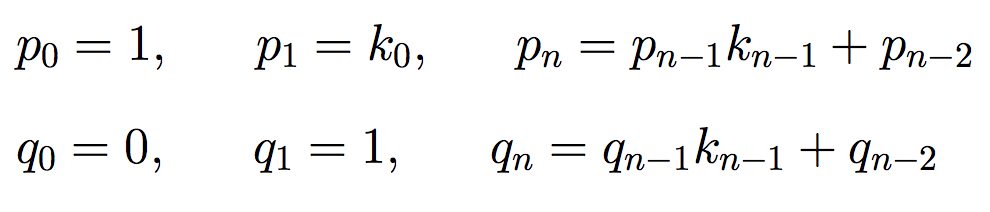容易に想像できるように, LとRの列RL0RLR2LRL4RLR6L ...は, 1年前のブログにあるeの連分数展開[2,1,2,1,1,4,1,1,6,1,1,8]と同じパターンである.

昔のブログの最後の方の中間近似分数にも同じ分数が現れる.

「コンピュータの数学」には無理数αからLとRの列を求める式もある.

if α < 1 then (output(L); α:=&alpha/(1-&alpha))
           else (output(R); α:=α-1)

途中のαと一緒にLとRを計算すると

from math import e
print(e)
alpha=e
lri=[]
def sb():
    global alpha
    if alpha<1:
        lri.append("L")
        alpha=alpha/(1-alpha)
    else:
        lri.append("R")
        alpha=alpha-1
    print(alpha)

for i in range(16):
    sb()
print(lri)

2.718281828459045
1.718281828459045
0.7182818284590451
2.5496467783038432
1.5496467783038432
0.5496467783038432
1.2204792856454296
0.22047928564542962
0.2828395468977148
0.39438809777395056
0.651222501282252
1.8671574389873726
0.8671574389873726
6.5277079301786785
5.5277079301786785
4.5277079301786785
3.5277079301786785
['R','R','L','R','R','L','R','L','L','L','L','R','L',
'R','R','R']

つまり連分数で1なら文字は1回, 2なら2回 繰り返すのであり, Stern Brocot木による計算は連分数展開の近似を, 中間近似分数まで含めて得ていたのであった.

連分数と近似分数

 昨年6月のブログで, eの近似分数 878/323の求め方を話題にした. 先月出版された「コンピュータの数学 第2版」を拾い読みしていたら, Stern Brocot木の関連でeの近似分数を求める話があった.

Stern Brocot木は, 互いに素なmとnの分数を大きさの順に並べたもので, 次のような形である. ある場所の値は, その左上の一番近い祖先m, nと右上の一番近い祖先m', n'から m+m'/n+n' で得られる.

最上部の1/1からLでは左下へ, Rで右下へ辿ると, 色々な分数が一意的に表せる. そしてeは

e=RL⁰RLR²LRL⁴RLR⁶L ...

つまりRL⁰R, LR²L, RL⁴R, LR⁶L, ...

であって, Eulerが24歳の時に発見したと書いてあった.

早速計算するプログラムをSchemeで書いた.

(l)は左下へ, (r)は右下へ進む関数. lmnは左祖先, rmnは右祖先, cmnは現在の分数, nmnは次の世代の分数である.

(define (show) (display cmn))
(define lmn '(0 1)) (define cmn '(1 1)) (define rmn '(1 0))
(define (reset!) (set! lmn '(0 1)) (set! cmn '(1 1))
  (set! rmn '(1 0)) (show))
(define (l) (let ((nmn (map + lmn cmn)))
 (set! rmn cmn) (set! cmn nmn) (show)))
(define (r) (let ((nmn (map + cmn rmn)))
 (set! lmn cmn) (set! cmn nmn) (show)))
(for-each (lambda (c)
 (cond ((eq? c 'l) (l))
       ((eq? c 'r) (r))
       (else (reset!))))
  '(c r r l r r l r l l l l r l r r r))

実行すると,

(1 1)(2 1)(3 1)(5 2)(8 3)(11 4)(19 7)(30 11)(49 18)(68 25)

(87 32)(106 39)(193 71)(299 110)(492 181)(685 252)

(878 323)

すげー.

連分数と近似分数

 
 
Martin GardnerがそのThe Unexpected Hanging(ネットで見つかる)の40ページで, 自然対数の底eを近似する, 分母分子とも3桁以内の分数は何かと問うている. その答は覚えやすい878/323 (=2.718266253869969...)だが, その計算法が今回の話題である.

Gardnerは自分では説明せず,
George Chrystal, Algebra An Elementary Text-Book for the Higher Classes of Secondary Schools and for Colleges, Part II. 1906
を見よとしか書いていない. この古典は有名らしく, ネットで探すと読むことができる. (648ページもある!)
http://www.archive.org/details/algebraelementar02chryuoft.pdf

しかしこれは, 高木貞治先生の「初等整数論講義」(手元のは第2版だが)の「中間近似分数」の章にそのものずばりの解説がある.

円周率πの同様な近似値355/113は遥かに有名であった. この分数を得るには連分数を使う.

普通の連分数は



の左上のような形である. この元のTexプログラムは

   \[a_0+{b_1\over\displaystyle a_1+
     {\strut b_2\over\displaystyle a_2+
       {\strut b_3\over\displaystyle\ddots+
         {\strut b_n\over a_n+\ddots
   }}}}\]
   \[a_0+\frac{b_1}{a_1}\:\raisebox{-1.3ex}{+}\:\frac{b_2}{a_2}
      \:\raisebox{-1.3ex}{+}\:\raisebox{-1.ex}{\ldots}\,
   \raisebox{-1.3ex}{+}\:\frac{b_n}{a_n}
   \raisebox{-1.3ex}{+}\:\raisebox{-1.ex}{\ldots}\]

この式にあるb_iを1, a_iを正の整数k_iにしたものを単純(simple)連分数とか正則(regular)連分数といい, 右上のように書き, 物の本にはこれだけを扱ううものが少くない.

こういう表示法は空間をとるので, 通常は下の左や右のように書く. k_iを部分商という.

こういう連分数から, 878/323や355/113のような近似分数が得られる.

円周率πの連分数展開で得られる部分商は7, 15, 1, 292, 1,...
で, この値を順に求める方法が「初等整数論講義」に載っている. これを見ると連分数は, Euclidの互除法に似ていることが分る.



部分商kの値から,


の関係でp, qが計算できる. πの場合のk, p, qは下の表の通り. p/qは連分数の展開を途中で止めたときの分数の値であり, 下の計算のようになる. 各行の右は, 左の分数の値とπとの差で, 見て分るように, 正負が交互に現れる.

この表の下の方に, 355/113がある. この近似分数はこうして発見された.


eについては, 今回はPythonで書いて

import math
x=math.e
ai=[]
while len(ai)<12:
    a=math.floor(x)
    ai.append(a)
    x=1/(x-a)
print(ai)

すると得られた結果は

[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8]


πと同じような表を作ると



しかしこの計算には, 問題の878/323がない. そこで「中間近似分数」が登場する.

 p₅=106, p₆=193,p₇=1264
q₅=39, q₆=71,q₇=465
の間には
p₇-p₅=p₆×k₆
q₇-q₅=q₆×k₆

の関係があるから, pの方は106に193を6回足すと1264になり, qは39に71を6回足すと465になる. この足し算の途中の値r_λ, s_λを分子, 分母にして計算すると, p₅/q₅からp₇/q₇の間の近似値が次々と得られる. これを中間近似分数(intermediate convergents)という.

この計算が次の表である.
    
    
    
そしてこの中に, 問題の878/323があったということだ.