SDGsロゴの錯視

貧困なし, 飢餓ゼロ, 健康と幸福, 高度の教育,...など, 2030年までの17達成目標を掲げる国連のSDGs(持続可能な開発目標 Sustainable Development Goals)のロゴはなかなか華麗だ. 早速PostScriptで描いてみた.





 
 













カラフルな17個の扇形で囲まれていて, その隣り同志の扇形の間には白い間隔がある. この間隔は等幅のようでもあるが, なんとなく内側の方が広く見えるから不思議だ. 扇形が内側で狭くなるのにつられて, 間隔は逆に内側が広く感じるのであろうか. これを取り敢えずSDGsロゴの錯視といおう.

そこだけ取り出して描いたのがこの図だ.





これだけ眺めると, 外縁での間隔g_oと, 内縁での間隔g_iは別に違っては見えないが, 上の図ではたしかに錯視が起きる.

北岡さんの錯視のカタログhttp://www.psy.ritsumei.ac.jp/~akitaoka/catalog.htmlを見たが, こんなに簡単なのは掲載されていないようだ.

間隔の幅Gを変えたり, 内縁半径Rを変えたりして, 錯視の起きる範囲をしらべたいと思い作ったウェブアプリが下だ. 左下は+, -でRを加減する. Rをクリックすると標準に戻る. 右下はGについての同様なメニューである.



錯視の起きる起きないの境界は微妙なので, はっきりしたことはいえないが, 錯視はほどほどの間隔の時に起き易いらしい. このウェブアプリは出来たばかりで枯れていないので, うまく動作しない時はご容赦を乞う.

Tパズル

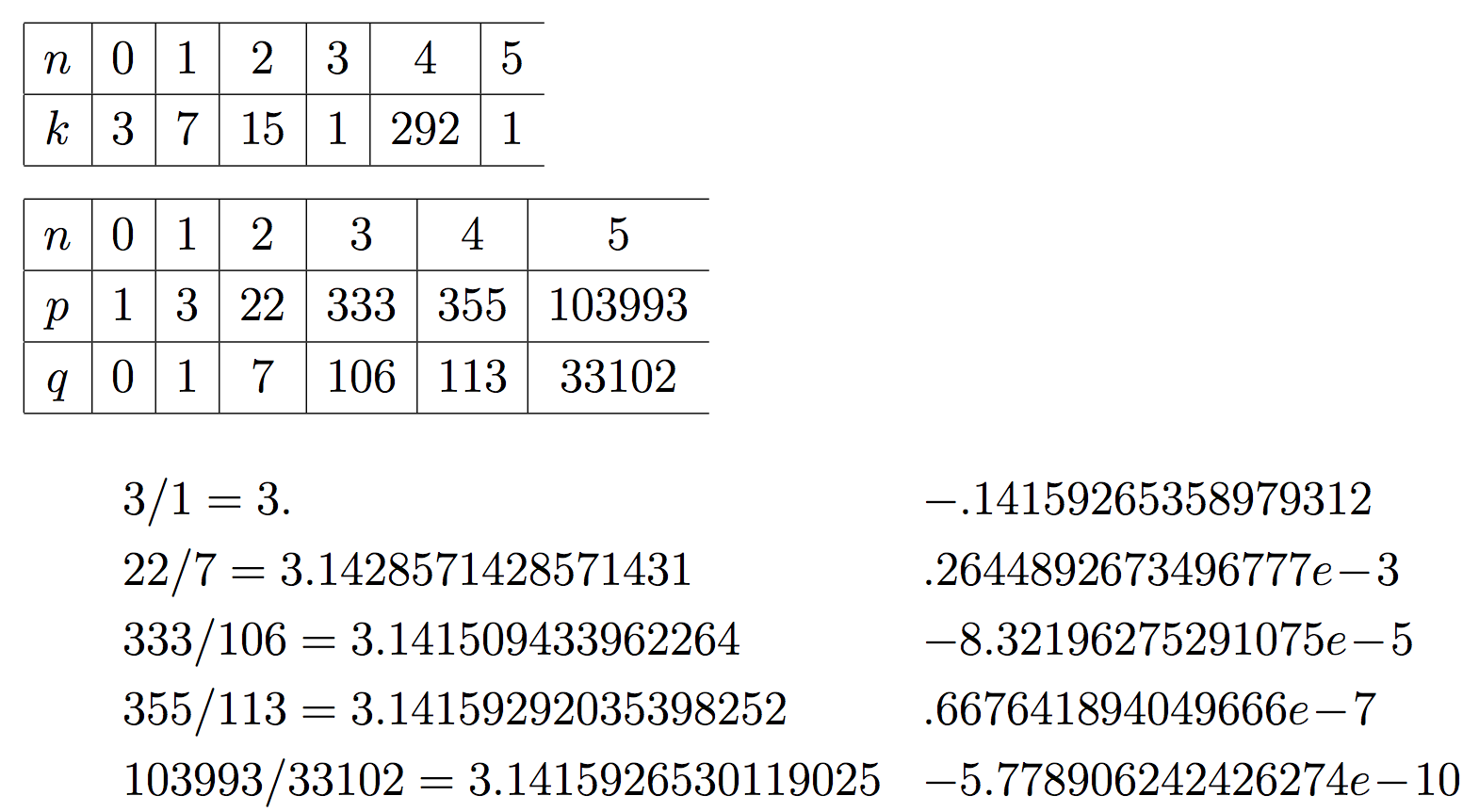
昨年夏のプログラミング・シンポジウムは諏訪のかんぽの宿で開催された. その客室にはお茶などと一緒にTパズルが置いてあり, それをいじった泊り客が気に入って宿の売店で購入するのを期待している.




Tパズルは上の図の左の家型の五角形を4分割したなんの変哲もないピースを組み合わせ, 指示されたいろいろな形を構成するパズルである. 最初の指示が図の右のT型を作るので, Tパズルというらしい. 元の家型の時のピースの縦横の辺が, T型では斜めになっているので, この問題は最初からいささか意地が悪い.

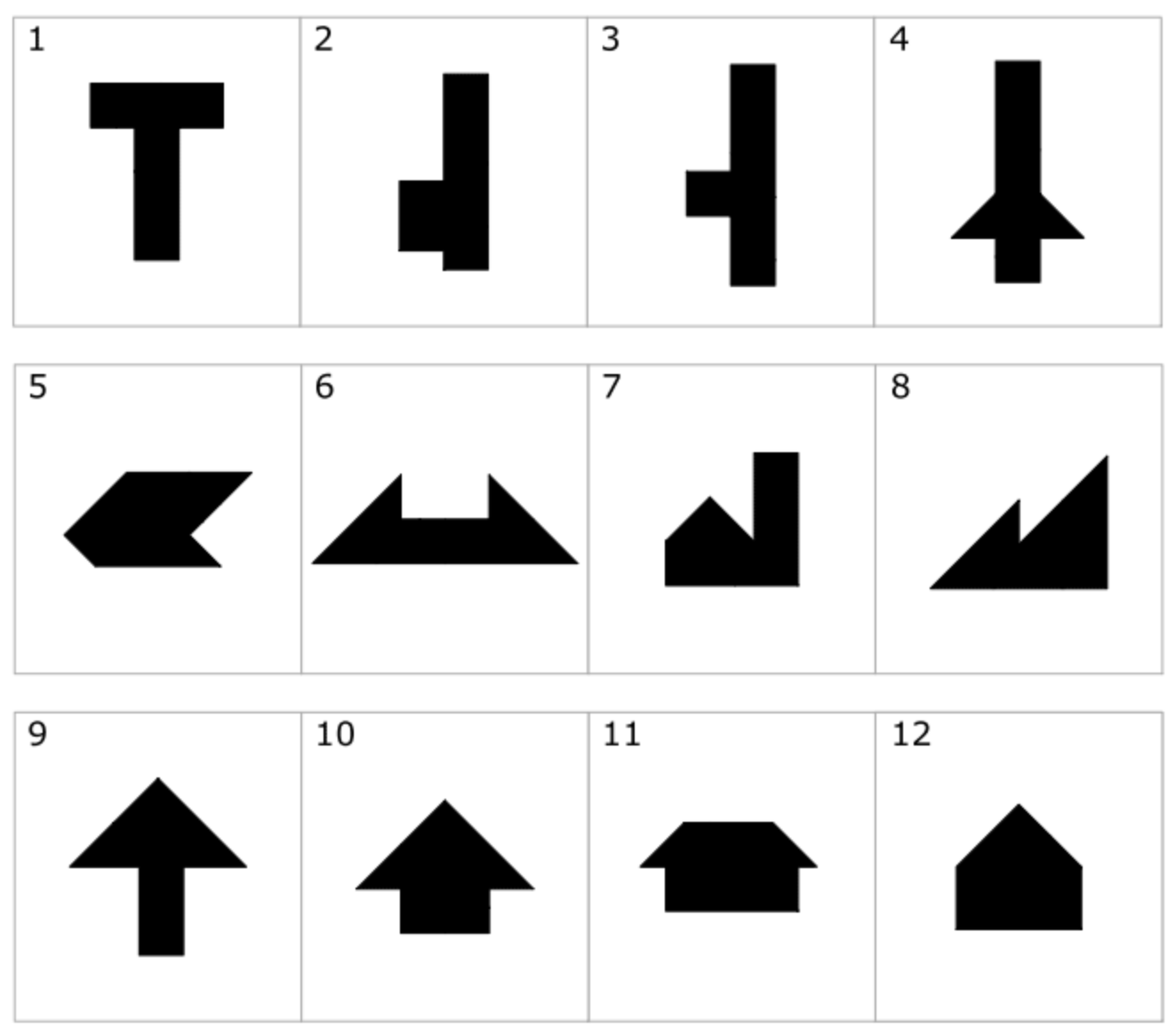
インターネットで探すと, 下の図のように様々な問題があるので, ちょっとやってみたくなり, 百円ショップで小学生の使う工作用紙を購入し, 自作した.


     
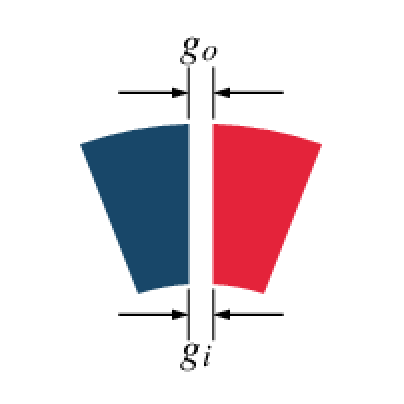
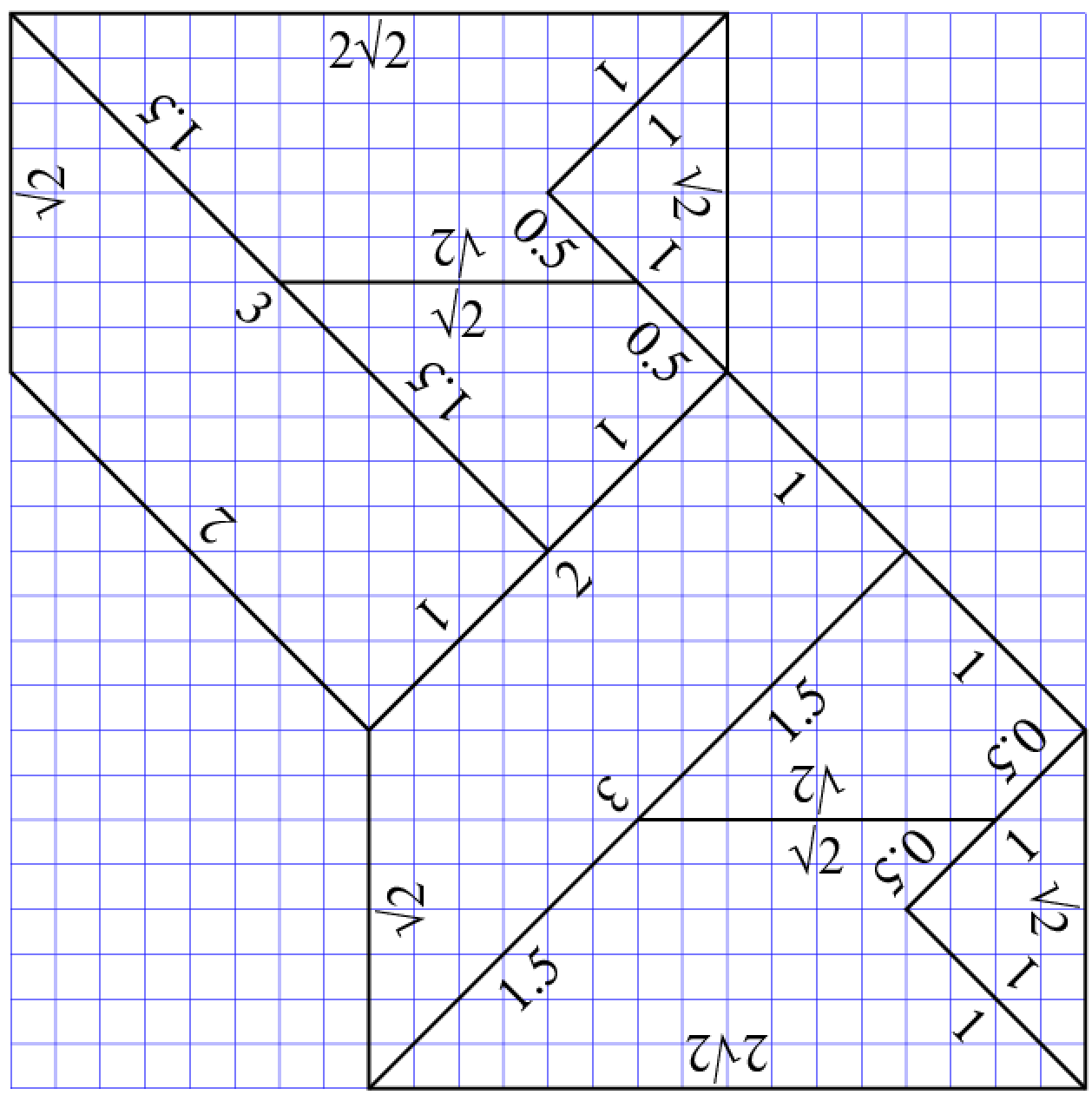
自作するには下のような図を描き, 同じ形の表と裏を貼り合せた. この升目が工作用紙の1cmである. 各辺の内側の数値は, T型の足の幅を基本単位とするその辺の長さで, 出来上がったピースにも同様に記入してある. この図では各ピースが繋って描いてあるが, 作業に便利なように, 本当はピースの間に隙間があった.



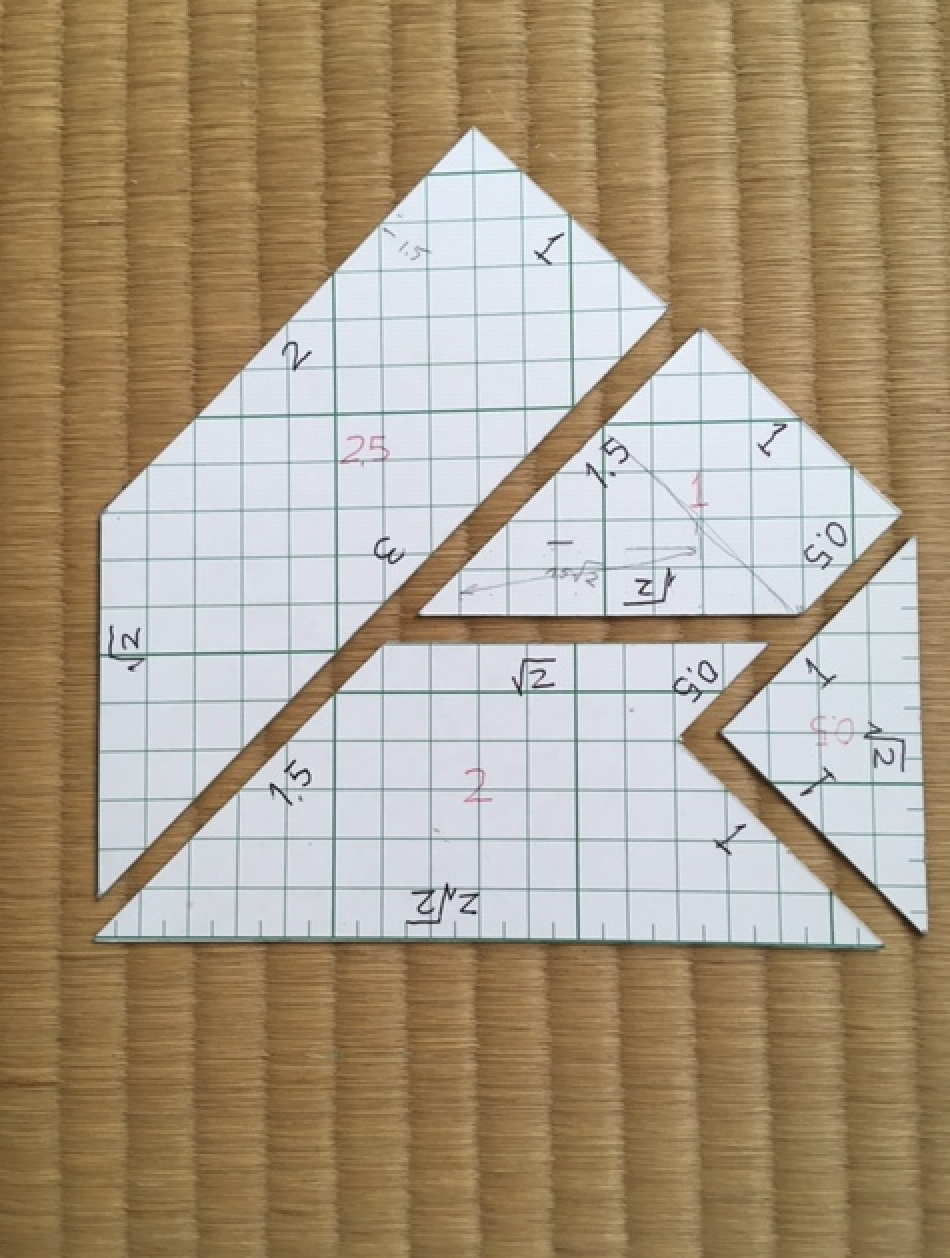
実際に出来たものは下の写真の通りで, 旅館で販売しているものより遥かに大きい. 市販のものは辺に寸法が書いてなく, いわばアナログ仕様だが, それでは√2と1.5の区別もつき難そうだ. 私のは寸法が記入してあるので間違うことはない.
    




さて, 私のやり方をちょっと種明かししよう. 上にあった問題の1番のT型と12番の家型を例にする.

型の図をPCに読み込み, 適当に拡大する. 角に順に番号をつける. マウスを動かし, それぞれの角の座標を読み取る. 座標はそれほどの精度を要求しない. それが下の2枚の図だ.




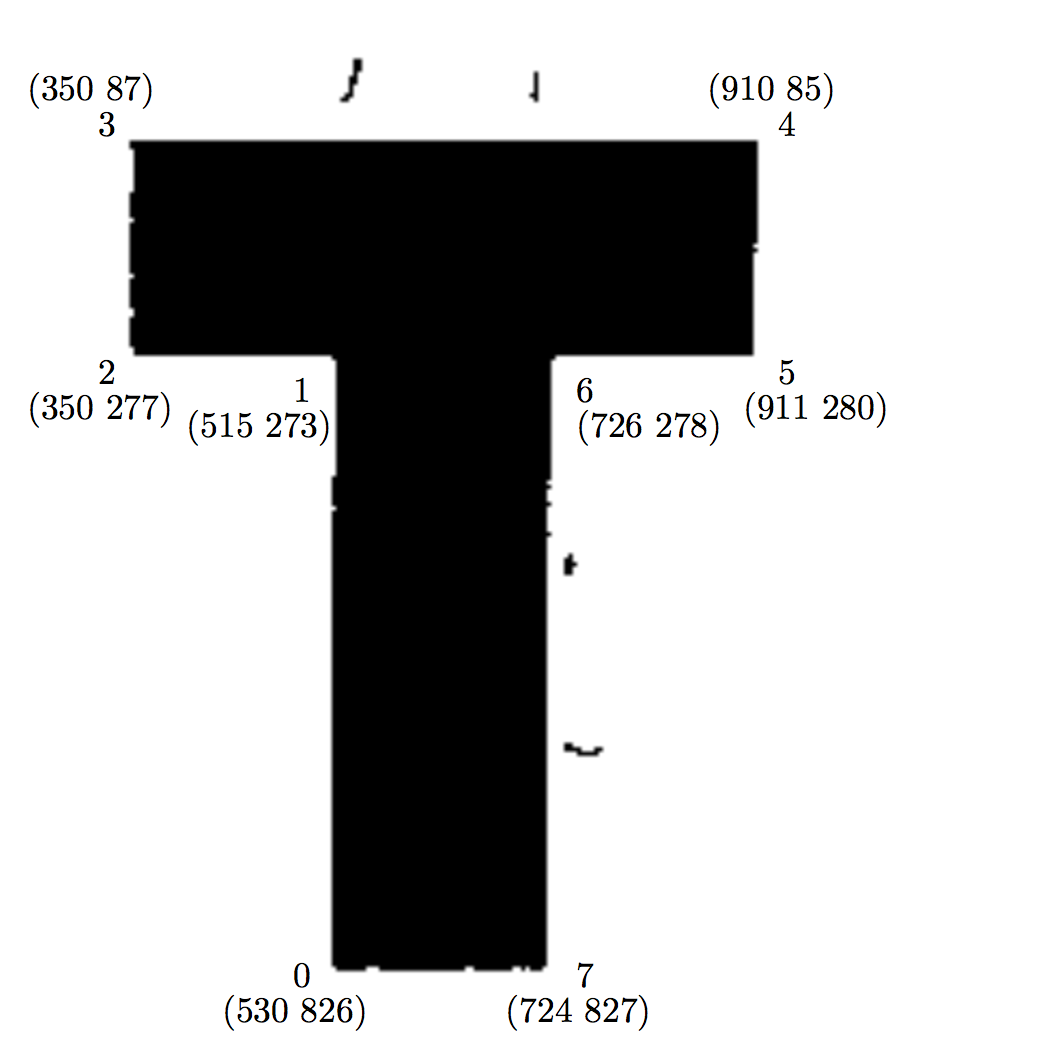
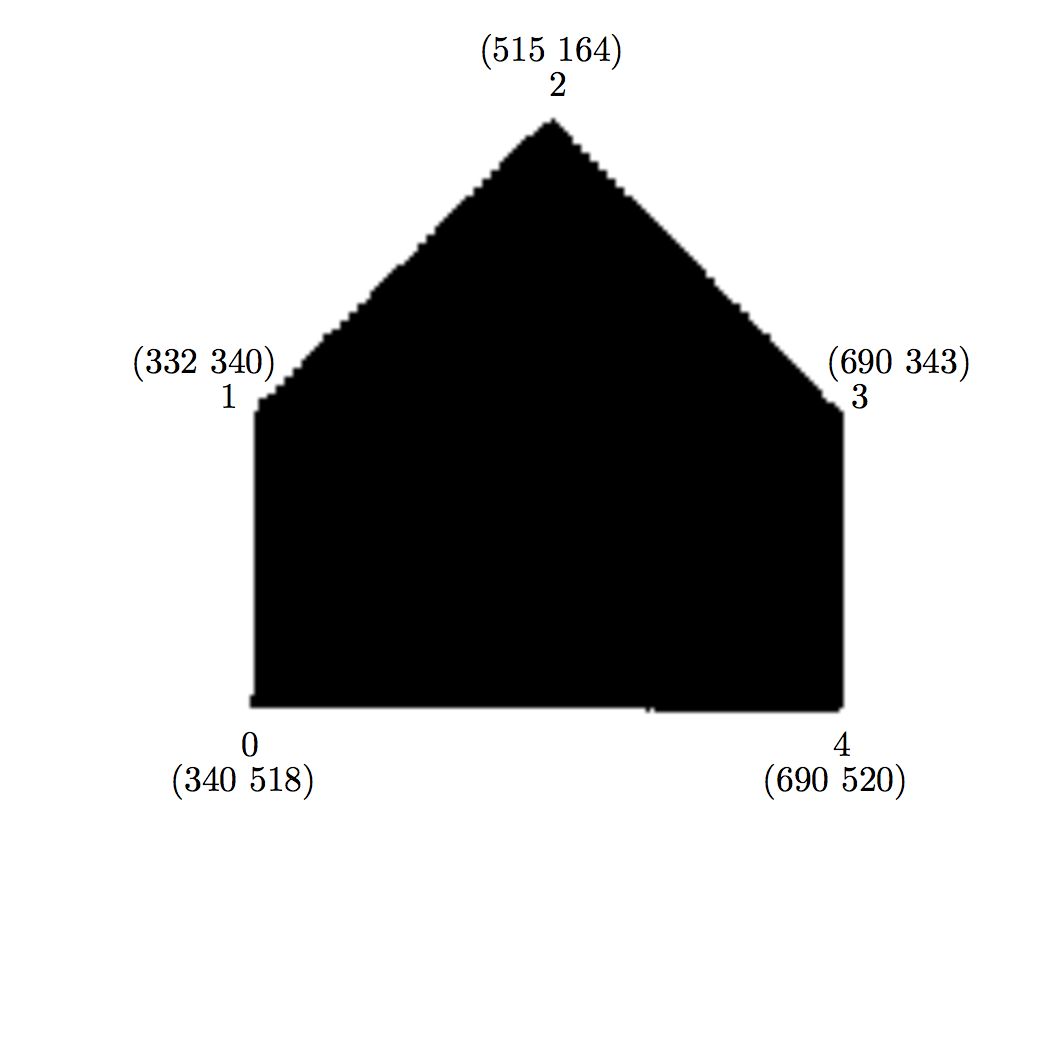
次にこの形を角を頂点とする三角形に分割する. T型では((0 6 7) (0 1 6) (4 5 6) (4 6 1) (4 1 2) (4 2 3)), 家型では((1 2 3) (1 3 4) (1 4 0))とした. そして夫々の型で, 座標と三角形の頂点の組をSchemeのプログラムで読み込む. その値を確認するため, プログラムはSchemeのgraphics機能を利用して出力する. それが次の図である. T型の足など多少怪しいがまぁよしとしよう.
   



   
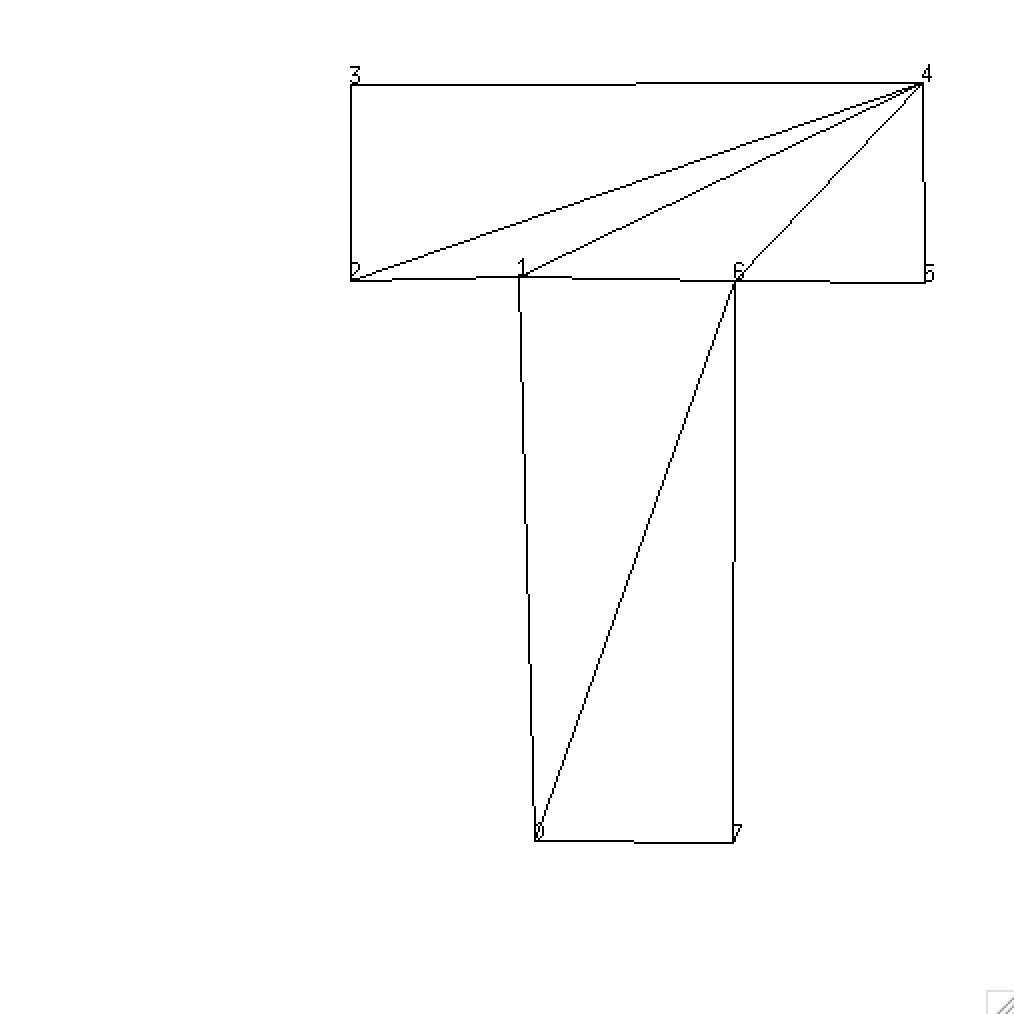
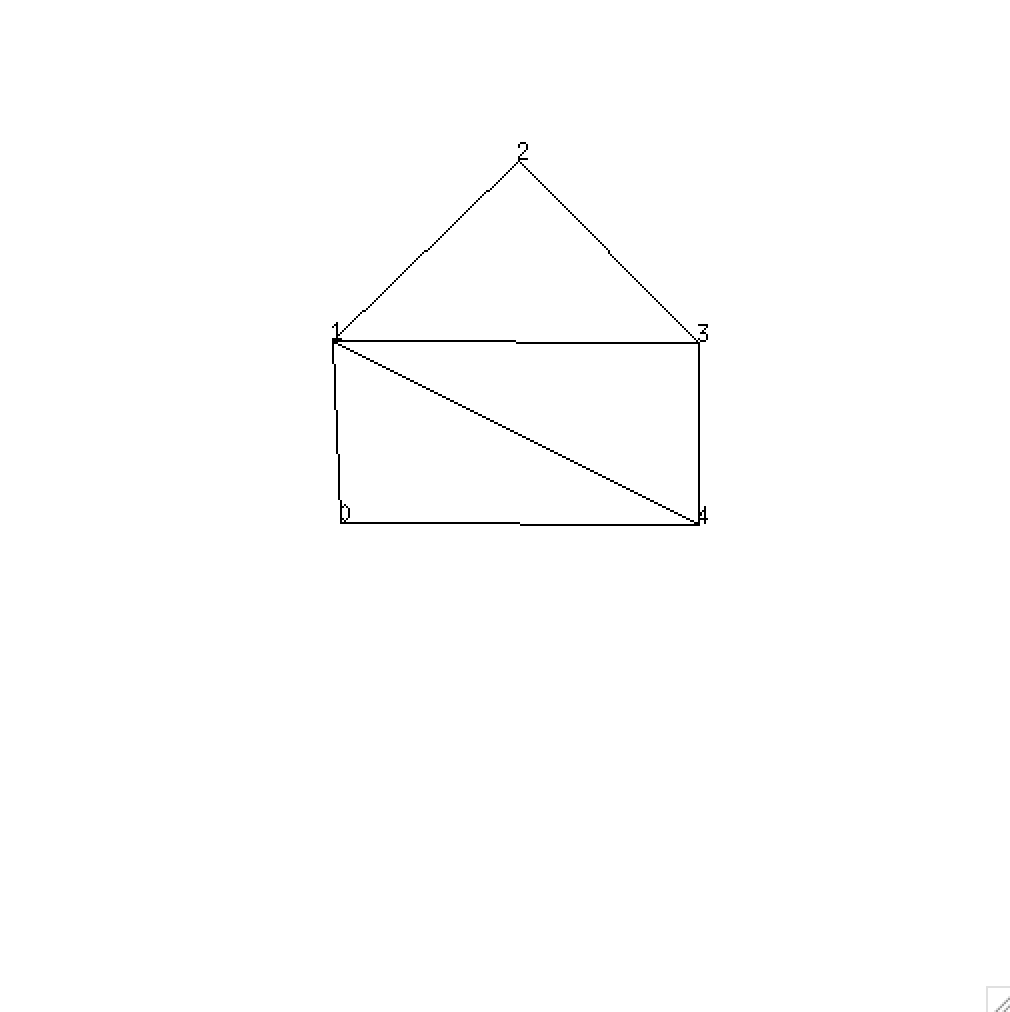
続いてこの座標系において相隣る2点間の距離を計算する. それぞれの点のx, y座標が既知だから, Pythagorasの定理で距離は分る. 更にこの座標系での各々の三角形の面積を求め, 形全体の面積を算出する.

x₀,y₀; x₁,y₁; x₂,y₂を頂点とする三角形の面積は, 行列式

|x₀ y₀ 1|
|x₁ y₁ 1|
|x₂ y₂ 1|

の半分であることは高校生のころ, 解析幾何の授業で学んだのでそれを使う. ただ三角形の頂点を時計廻りか反時計廻りかで辿ると面積が正負になり, いつも怪しくなる. そういう時は(0,0) (1,0) (0,1)の三角形で試みると反時計廻りで正になると分るが, プログラムでは絶対値をとってから合計している.

一方, 4個のピースの面積の和は6平方基本単位であるから, 今得られた面積を6で除して平方根をとると, それが座標系の長さと基本単位の比で, それぞれの辺が基本単位に変換できる.

これでT型を計算すると
(2.8999986101772106 .8652158634699881 .9960165420683874 2.935646424994157 1.0222409451321806 .9698622511287074 2.8779826845214163 1.0169988220903106)
が出てきて, 番号0の角からの順の辺の長さが, 3,1,1,3,1,1,3,1であることが分る. (0.865を1にするには勇気がいるが.)

また家型の方は
(1.418992855950106 2.022013340831029 1.993599932770006 1.4095980475184093 2.7873862791620128)
だから, √2, 2,2,√2, 2√2らしいとなる.

ここまで来たら大体の問題はわけもなく解けるが, 実際にやってみると案外微妙な値になる型もあり(1.5か√2かなど), ここに述べた方法が特効薬であるわけでもない. 元々の問題の図もさほど精密ではなく, また中にはこれはどうかと思う問題もあったが, 目くじらを立てることもあるまい.

連分数と近似分数

 
 
Martin GardnerがそのThe Unexpected Hanging(ネットで見つかる)の40ページで, 自然対数の底eを近似する, 分母分子とも3桁以内の分数は何かと問うている. その答は覚えやすい878/323 (=2.718266253869969...)だが, その計算法が今回の話題である.

Gardnerは自分では説明せず,
George Chrystal, Algebra An Elementary Text-Book for the Higher Classes of Secondary Schools and for Colleges, Part II. 1906
を見よとしか書いていない. この古典は有名らしく, ネットで探すと読むことができる. (648ページもある!)
http://www.archive.org/details/algebraelementar02chryuoft.pdf

しかしこれは, 高木貞治先生の「初等整数論講義」(手元のは第2版だが)の「中間近似分数」の章にそのものずばりの解説がある.

円周率πの同様な近似値355/113は遥かに有名であった. この分数を得るには連分数を使う.

普通の連分数は



の左上のような形である. この元のTexプログラムは

   \[a_0+{b_1\over\displaystyle a_1+
     {\strut b_2\over\displaystyle a_2+
       {\strut b_3\over\displaystyle\ddots+
         {\strut b_n\over a_n+\ddots
   }}}}\]
   \[a_0+\frac{b_1}{a_1}\:\raisebox{-1.3ex}{+}\:\frac{b_2}{a_2}
      \:\raisebox{-1.3ex}{+}\:\raisebox{-1.ex}{\ldots}\,
   \raisebox{-1.3ex}{+}\:\frac{b_n}{a_n}
   \raisebox{-1.3ex}{+}\:\raisebox{-1.ex}{\ldots}\]

この式にあるb_iを1, a_iを正の整数k_iにしたものを単純(simple)連分数とか正則(regular)連分数といい, 右上のように書き, 物の本にはこれだけを扱ううものが少くない.

こういう表示法は空間をとるので, 通常は下の左や右のように書く. k_iを部分商という.

こういう連分数から, 878/323や355/113のような近似分数が得られる.

円周率πの連分数展開で得られる部分商は7, 15, 1, 292, 1,...
で, この値を順に求める方法が「初等整数論講義」に載っている. これを見ると連分数は, Euclidの互除法に似ていることが分る.



部分商kの値から,


の関係でp, qが計算できる. πの場合のk, p, qは下の表の通り. p/qは連分数の展開を途中で止めたときの分数の値であり, 下の計算のようになる. 各行の右は, 左の分数の値とπとの差で, 見て分るように, 正負が交互に現れる.

この表の下の方に, 355/113がある. この近似分数はこうして発見された.


eについては, 今回はPythonで書いて

import math
x=math.e
ai=[]
while len(ai)<12:
    a=math.floor(x)
    ai.append(a)
    x=1/(x-a)
print(ai)

すると得られた結果は

[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8]


πと同じような表を作ると



しかしこの計算には, 問題の878/323がない. そこで「中間近似分数」が登場する.

 p₅=106, p₆=193,p₇=1264
q₅=39, q₆=71,q₇=465
の間には
p₇-p₅=p₆×k₆
q₇-q₅=q₆×k₆

の関係があるから, pの方は106に193を6回足すと1264になり, qは39に71を6回足すと465になる. この足し算の途中の値r_λ, s_λを分子, 分母にして計算すると, p₅/q₅からp₇/q₇の間の近似値が次々と得られる. これを中間近似分数(intermediate convergents)という.

この計算が次の表である.
    
    
    
そしてこの中に, 問題の878/323があったということだ.