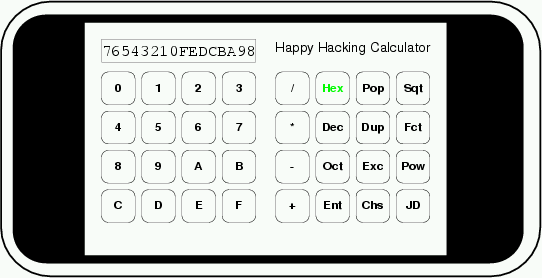
数日前に書いた個人用電卓にユリウス日のキーがあった. これは特に週日を求めるためのものである. ユリウス日に1を足し, 7で法をとると日曜を0, 月曜を1, ..., 土曜を6とする週日が得られるのである. またこの電卓は, 除算のとき, スタックトップには商が, そのすぐ下には剰余が出るので, 20081020 [JD] 1 [+] 7[/] [Pop] -> 1 となり, 本年10月20日は月曜と分かる.
-4712年1月1日も月曜であったわけだ.
ユリウス日は, -4712年1月1日 世界時正午を0.0とし, それからの通日である. 2008年10月20日のユリウス日が2454760というのは, 正確にはその日の世界時正午, JSTで午後9時のユリウス日が2454760.0であるということだ. それを省略してその日のユリウス日という. -4712年1月2日のユリウス日は1である.
理科年表や天文年鑑にも計算用の表がある.
A表 B表 * C表 *
-1000 1355808 0 0,-1 1 0 0
-900 1392333 1 365 2 31 31
-800 1428858 2 730 3 59 60
... 3 1095 4 90 91
1300 2195883 4 1460 ...
1400 2232408 5 1826 11 304 305
1500 2268933 ... 12 334 335
1500 2268923 98 35794
1600 2305448 99 36159
...
2000 2451545
例えば2004年4月23日のユリウス日ならA表から2000年の2451545, B表から4年の1460, C表から4月の右の閏年用の91をとり, それに23を足して(+ 2451545 1460 91 23) -> 2453119が得られる.
このA表は, 例えば2000年なら, -4712年1月1日から1999年12月31日までの日数である. 従ってこれは2001年1月1日のユリウス日のになりそうだが, B表の最初0年に, 閏年なら-1, 平年なら0とあるのが重要で, 2000年は閏年なので, 1引くから結局1月0日のユリウス日になる.
変換の式もサーチエンジンで探せるが, 私が情報処理学会誌のHaskell Programmingに書いた,
mon0, mon1 :: [Int]
mon0 = [0, 31, 59, 90, 120, 151, 181, 212, 243, 273, 304, 334]
mon1 = [0, 31, 60, 91, 121, 152, 182, 213, 244, 274, 305, 335]
gleap, jleap :: Int -> Bool -- Gregorian, Julian暦のうるう年
gleap y = if y `mod` 100 == 0 then y `mod` 400 == 0
else y `mod` 4 == 0
jleap y = y `mod` 4 == 0
julianDate :: Int -> Int -> Int -> Int
julianDate y m d = -- aからgは途中の値
let a = (y + 4712) * 365
b = (y + 4712 + 3) `div` 4
c = if y > 1601 then y' `div` 400 - y' `div` 100 else 0
where y' = y - 1601
e = if [y,m,d] >= [1582,10,15] then -10 else 0
f = (if leap y then mon1 else mon0) !! (m - 1)
where leap = if y > 1600 then gleap else jleap
g = d - 1
in a + b + c + e + f + g -- 最後の結果
のようにも書ける.
インターネットなら,
https://www.onlineconversion.com/julian_date.htmにJulian Date Converterがあり, Year, Month, Day(, Hour, Minute, Second)を入れ, Computer Julian dateを押すと結果が返ってくる.
個人用電卓では結局上の式を使った.
電卓は実はやっとiPod touchに実装した. 電車の中でもテストが出来て楽しいが, 実用化にはまだ改良の余地は多々ある.